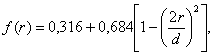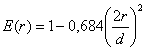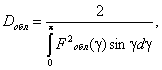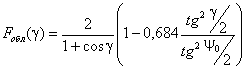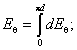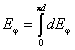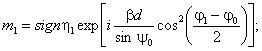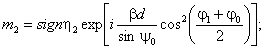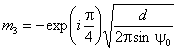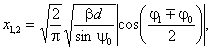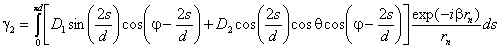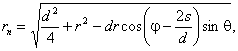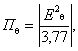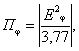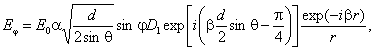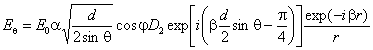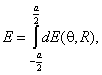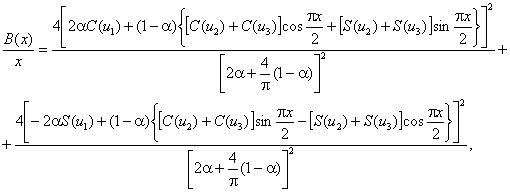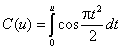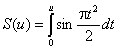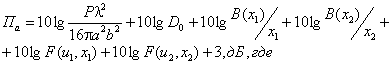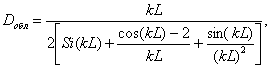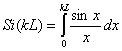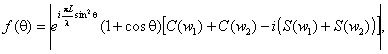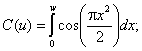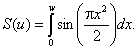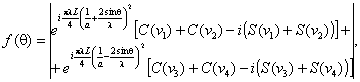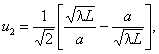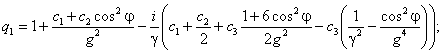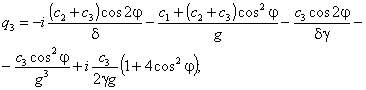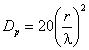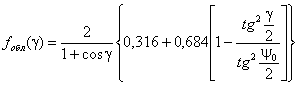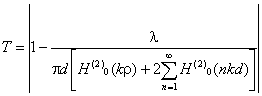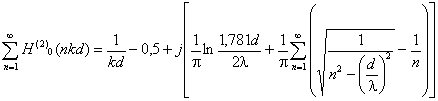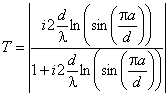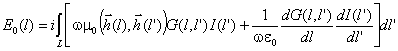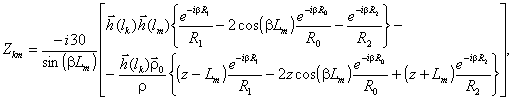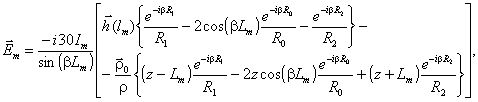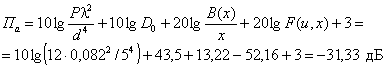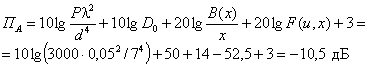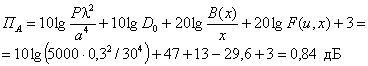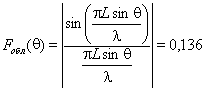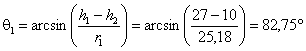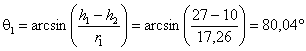|
|
Государственное
санитарно-эпидемиологическое
нормирование 4.3. МЕТОДЫ КОНТРОЛЯ. ФИЗИЧЕСКИЕ ФАКТОРЫ Определение плотности потока энергии Методические указания Минздрав России Москва 2002 1. Разработаны сотрудниками Самарского отраслевого
научно-исследовательского института радио Министерства Российской Федерации по
связи и информатизации (Бузовым А. Л., Кольчугиным Ю. И., Кубановым В. П., Романовым В. А.,
Сподобаевым Ю. М., Филипповым Д. В., Юдиным
В. В.). 2.
Представлены Минсвязи России письмом от 20.04.01 № НТУ-1/237. Одобрены комиссией по государственному
санитарно-эпидемиологическому нормированию при Минздраве России. 3.
Утверждены и введены в действие Главным государственным санитарным врачом
Российской Федерации 7 октября 2002 года. 4.
Введены взамен методических указаний «Определение плотности потока излучения
электромагнитного поля в местах размещения радиосредств, работающих
в диапазоне частот 700 МГц - 300 ГГц. МУК
4.3.680-97». Редакторы
Барабанова Т. Л., Максакова Е. В. Технический
редактор Ломанова Е. В. СОДЕРЖАНИЕ УТВЕРЖДАЮ Главный государственный санитарный врач Российской Федерации -
Первый заместитель Министра здравоохранения Российской Федерации Г. Г. Онищенко 7 октября 2002 г. МУ
4.3.1167-02 Дата введения: с момента утверждения 4.3. МЕТОДЫ
КОНТРОЛЯ. ФИЗИЧЕСКИЕ ФАКТОРЫ Определение плотности потока энергии электромагнитного поля в
местах размещения радиосредств, работающих в диапазоне частот 300 МГц - 300 ГГц Методические
указания Область применения
Методические
указания содержат изложение методики мониторинга окружающей среды вблизи антенн
радиосредств, работающих в различных участках диапазона частот 300 МГц-300 ГГц, по электромагнитному фактору. Являются
государственным методическим документом для определения санитарно-защитных зон и зон
ограничения застройки, а также для прогнозирования уровней электромагнитного
поля при выборе мест размещения радиосредств. Предназначены
специалистам органов и учреждений санитарно-эпидемиологической службы,
проектных организаций, операторам связи. Документ
введен взамен МУК 4.3.680-97. Отличается от прежнего документа тем,
что распространяется на более широкий класс антенн, содержит рекомендации по
учету решетчатой структуры антенного рефлектора, влияния земли и крыши на
величину плотности потока энергии в расчетной точке. Не
распространяется на радиосредства базовых станций систем подвижной связи и
станций телевизионного вещания. 1. Радиосредства
На
частотах выше 300 МГц работают различные радиосредства: радиорелейные системы
передачи прямой видимости (РРСП ПВ), тропосферные радиорелейные системы
передачи (ТРРСП),
спутниковые системы передачи (ССП), радиолокационные станции (РЛС). Передающая
часть любого радиосредства имеет антенну - устройство преобразования энергии,
вырабатываемой радиопередатчиком, в энергию свободно распространяющихся
радиоволн. Наиболее распространенными на практике являются апертурные
антенны - вырезки из параболоида вращения (с круглой, квадратной, прямоугольной
апертурой), рупорно-параболические антенны, перископические антенные системы, а
также вибраторные антенны. Реже (в качестве
самостоятельных) применяются рупорные антенны,
антенны в виде вырезки из параболического цилиндра. Каждая антенна имеет
характерные элементы, определяющие конструкцию. Для антенн, построенных на
основе вырезки из параболоида вращения, это рефлектор (зеркало с
соответствующей формой апертуры) и облучатель, расположенный, как правило, в
фокусе параболоида. Рупорно-параболическая антенна - это единая конструкция в
виде двух совмещенных элементов: рупора и несимметричной вырезки из параболоида
вращения Перископическая антенная система имеет три основных элемента:
первичный облучатель (как правило, рупорный), нижнее зеркало и верхнее зеркало.
Рупорная антенна состоит из отрезка волновода постоянного сечения и собственно
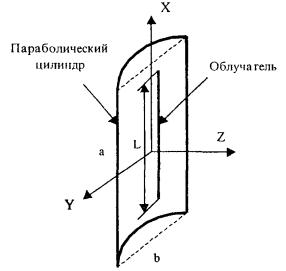
рупора, представляющего собой волновод с плавно увеличивающимся сечением. Антенна типа параболический цилиндр -
это апертурная антенна с рефлектором в виде
параболического цилиндра и линейным источником возбуждения. Антенны вибраторной
конструкции - это совокупность активных и пассивных излучателей. Основными
данными, необходимыми для расчета электромагнитной обстановки вблизи
радиосредства, являются: мощность передатчика, рабочая частота (длина волны),
КНД антенны, пространственное положение и геометрические размеры излучающих
элементов. 2. Расчет плотности потока энергии вблизи
параболических антенн с круглой апертурой
Общие
положения. Значение плотности потока энергии (ППЭ) апертурной антенны в
произвольной точке пространства (в рамках энергетического подхода к решению
задачи) определяется по формуле: ПΣ = Па + Побл + Пдиф + Ппр, где (2.1) Па
- апертурная составляющая; Побл - составляющая,
определяемая излучением облучателя; Пдиф - составляющая,
обусловленная токами, протекающими вблизи кромки зеркала (дифракционными
токами); Ппр
- составляющая, возникающая в результате прохождения энергии сквозь
основное зеркало антенны, если оно имеет решетчатую структуру. Все
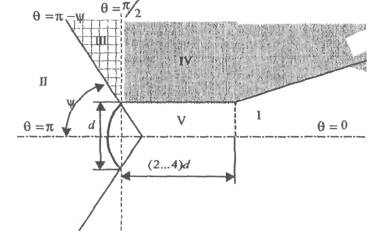
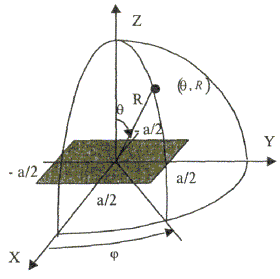
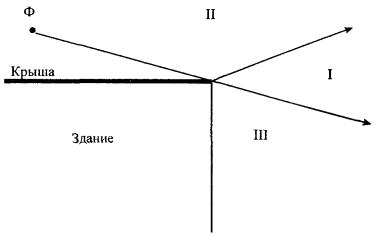
пространство вблизи антенны условно делится на ряд характерных областей,
которые ввиду симметрии показаны на рис. 2.1 только в секторе
углов 0 £ θ £ π. Рис. 2.1. Области анализа ППЭ. Значение
ППЭ в области I определяется апертурной составляющей Па и
составляющей облучателя Побл. В
области II - заднем полупространстве
антенны - ППЭ определяется составляющей Пдиф. Если зеркало
выполнено в виде решетчатой структуры, то к дифракционному полю добавится поле,
прошедшее в область II сквозь ячейки
решетки - составляющая Ппр. В
области III необходимо учитывать составляющие
Побл и Пдиф. Область III в заднем полупространстве существует только для
длиннофокусных антенн, когда ψ £ π/2. В
области IV ППЭ определяется в
основном составляющими Побл и Пдиф, но следует учитывать
и Па (особенно вблизи границы раздела областей I и IV). Область
V является областью конструкции антенны и
находится внутри гипотетического цилиндра с площадью основания, равной площади
апертуры и высотой 2...4 диаметра апертуры (эту область иногда
называют областью прожекторного луча). Используемые
допущения: · амплитудное
распределение поля по апертуре задается в виде «параболы на пьедестале»: r - текущее значения координаты на диаметре апертуры, d - диаметр апертуры; · облучатель и
антенна имеют характеристики направленности с осевой симметрией относительно
направлений их максимального излучения; · характеристика
направленности облучателя вне сектора углов перехвата энергии основным зеркалом
считается неизменной и равной 0,316 по напряженности поля
(по мощности 0,1); · апертура имеет
затенение, характеризуемое коэффициентом затенения dT / d = 0,1 (dT - диаметр «теневого диска», d - диаметр апертуры). Расчет
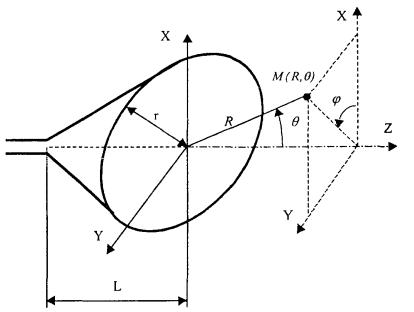
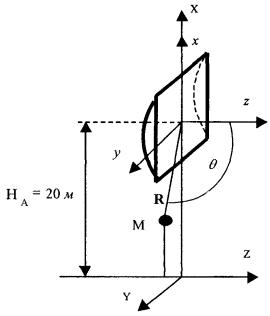
плотности потока энергии в области I. Плотность потока энергии в расчетной точке М (рис. 2.2) представляется в виде двух
составляющих: ПΣ = Па + Побл, где Па - апертурная
составляющая ППЭ (рис. 2.2а); Побл - составляющая
ППЭ, определяемая непосредственно излучением облучателя (рис. 2.2, б). В
предположении осевой симметрии характеристик направленности апертуры и
облучателя составляющие ППЭ имеют вид: Р -
мощность, излучаемая антенной, Вт; D0 - КНД антенны в
направлении максимального излучения в дальней зоне (величина безразмерная); B2 (R) - функция, учитывающая
зависимость КНД от расстояния; F2 (θ, R) - нормированная характеристика направленности антенны по
мощности; (θ, R) - сферические
координаты расчетной точки; Dобл - КНД
облучателя в направлении максимального излучения; F2обл (γ) -
нормированная характеристика направленности облучателя по мощности (угол γ
= 180° - θ). Рис. 2.2. К расчету апертурной составляющей ППЭ (а) и составляющей ППЭ облучателя (б). Электрические
параметры апертуры - характеристика направленности и КНД - являются функциями
расстояния R, а те же параметры облучателя не
зависят от R - считается, что
расчетная точка по отношению к облучателю всегда находится в дальней зоне. Вводятся
переменные: и - обобщенная угловая координата, х - относительное
расстояние: u = (πd sin θ) / λ, (2.5) х = R / Rгp, где (2.6) d - диаметр
апертуры, м; λ - длина волны, м; Rгр = 2d2 / λ - граничное расстояние, начиная с которого
можно считать, что расчетная точка находится в дальней зоне. С
учетом введения обобщенных координат выражение (2.3) принимает вид:
Перевод
размерности ППЭ Вт/м2 в мкВт/см2 осуществляется
в (2.7) умножением на 100. Переход
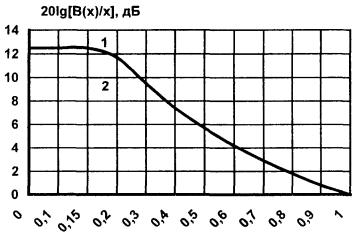
от абсолютных значений величины ППЭ к относительным (децибелам относительно 1 мкВт/см2) осуществляется по формуле: В(х) - функция, учитывающая изменение КНД в
зависимости от относительного расстояния; F(u, x) - нормированная
характеристика направленности апертуры в обобщенных координатах и,
х. С
учетом принятых допущений выражение (2.4)
при переходе к относительным значениям (децибелам относительно 1 мкВт/см2) приводится к виду: Аналитическое
выражение функции В(х)/х для круглой апертуры с амплитудным
распределением типа (2.2) имеет вид:
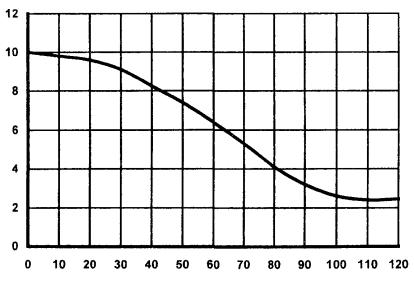
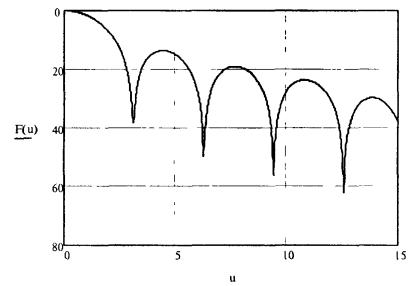
В
области х < 0,105 функция (2.10) сильно
осциллирующая, а в области х > 0,105
- изменяется монотонно. Осциллирующую часть функции следует заменить огибающей
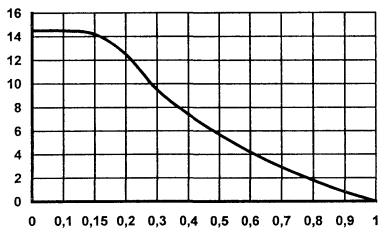
ее максимумов. На
рис. П1.1 (приложение 1) приведена функция На
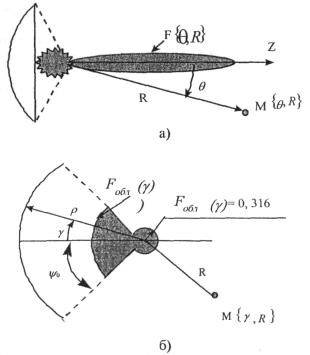
рис. 2.3 показана круглая апертура
с центральным затенением (затенение моделируется отсутствием элементов Гюйгенса
в центре апертуры - светлый круг). Поле в точке М является
суперпозицией полей элементов Гюйгенса dS, расположенных на поверхности раскрыва
(апертуре). Рис. 2.3. К расчету функции F(u, x). Напряженность
электрического поля, создаваемая в расчетной точке М всей
совокупностью элементов Гюйгенса, находящихся в апертуре, определяется следующей
формулой:
В (2.12) геометрические параметры θs, φs, rs являются функциями θ и R. Нормированная
характеристика направленности апертуры имеет вид:
В
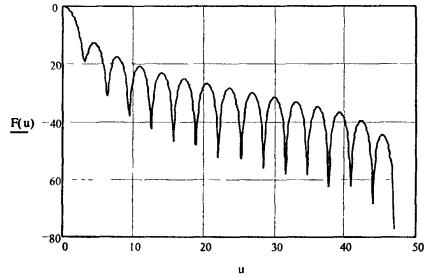
терминах координат u, x направленные свойства апертуры характеризуются функцией F(u, x). Процесс расчета
каждой функции F(u, x) требует
значительных вычислительных затрат, которые быстро растут с увеличением
отношения d/λ.
Функции F(u, x) сильно
осциллирующие, поэтому в практических расчетах ППЭ следует
использовать их гарантированные огибающие. Для удобства практических расчетов гарантированные огибающие
табулированы (приложение 1, таблицы 1.1
и 1.2). При значениях х
> 1, что
соответствует дальней зоне, необходимо пользоваться огибающими для x = 1. Значение
КНД облучателя рассчитывается по формуле: Fобл (γ) = 0,316 для
ψ0 < γ ≤
π · характеристика
направленности облучателя, реализующая амплитудное распределение вида (2.2) и обеспечивающая уровень 0,316
вне сектора углов перехвата энергии зеркалом (ψ0 £ γ
≤ π). Термин
«облучатель» следует понимать, как собственно облучатель в однозеркальной
антенне, так и систему «облучатель - вспомогательное зеркало» в двухзеркальной
антенне. График
зависимости D = 10 lg Dобл,
как функции аргумента ψ0 для усредненной модели антенн приведен
на рис. П1.2
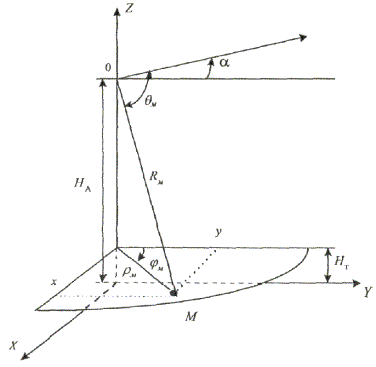
(приложение 1). Постановку
задачи при расчете ППЭ в области I вблизи антенны
с круглой апертурой иллюстрирует рис. 2.4,
на котором центр апертуры - это О, а его высота над землей - НА. Угол α характеризует
отклонение направления максимального излучения от плоскости горизонта. Ось Y системы координат XYZ совмещена с проекцией направления максимального излучения на
плоскость XOY. Горизонтальная плоскость, на
которой определяется ППЭ, находится на высоте НТ над землей.
Расчетная точка задается либо через координаты ρM (расстояние до
точки М вдоль поверхности земли) и φM, либо через у
и х. Рис. 2.4. Постановка задачи. Заданными
параметрами считаются: Р - мощность передатчика радиосредства, Вт; λ - длина волны, м;
d - диаметр
апертуры, м; D0 - КНД антенны в
направлении максимального излучения в дальней зоне; 2ψ0 - угол раскрыва антенны (угол перехвата
энергии облучателя зеркалом). В
области I порядок расчета следующий: 1. Вычисляется расстояние от центра апертуры до расчетной
точки М:
2.
Рассчитывается угол между направлением максимального излучения и направлением
линии «центр апертуры - расчетная точка M»: θM = arc cos {[ρM cos φ cos α - (HA - HT) sin α] / RM} (2.18) 3.
Определяется граничное расстояние Rгp: Rгр = 2d2 / λ (2.19) 4.
Вычисляются параметры u, x по формулам: u = (πd sin θ)
/ λ и x = R / Rгр (2.20) 5.
Находится значение функции 6.
Вычисляется значение функции 20 lg F(u, x), дБ (по огибающей). 7.
По формуле (2.8) рассчитывается
значение составляющей Па: 8.
Определяется: Dобл, дБ = 10
lg Dобл, (2.22) 9.
По формуле (2.9) находится значение
составляющей Побл: 10. Значение суммарной ППЭ рассчитывается по формуле: Методика
и порядок расчета имеют ограничение по минимальному удалению расчетной точки от
центра апертуры - Rmin ≥ d/2, что соответствует значению х
≥ Расчет
ППЭ для относительных расстояний х < Пs = 10
lg [400 P / (πd2 0,65)]
≈ 10 lg [200 P / d2], дБ (2.25) При
этом интерполяционная формула имеет вид: Повторяя
операции, предусмотренные порядком расчета ППЭ, последовательно для
различных точек выбранного азимута φ = const определяется характер изменения ППЭ
вдоль данного азимута, а также отыскивается точка, где значение ППЭ равно
предельно допустимому уровню. Совокупность подобных точек на других
азимутальных линиях, проведенных, например, через 1°, определяет границу
соответствующей санитарной зоны в области I. Расчет
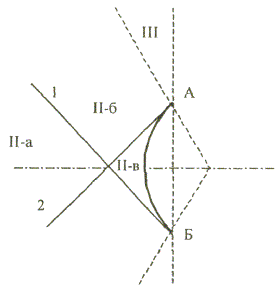
плотности потока энергии в области II. В области II поле
обусловлено дифракцией электромагнитных волн на кромке параболического зеркала.
Однако область II имеет три характерных подобласти
(рис. 2.5), которые образуются
после проведения двух касательных (1 и 2) в точках А и Б. Из подобласти II-а видна вся кромка антенны, из подобласти II-б видна часть кромки, из подобласти II-в кромка вообще не видна. Исходными
данными для расчета являются следующие параметры радиосредства: мощность
излучения Р, Вт; длина волны λ, м; диаметр антенны d, м; половина угла раскрыва
зеркала ψ0; коэффициент
использования поверхности зеркала kun; α - уровень напряженности электрического поля на кромке зеркала.
Постановка задачи иллюстрируется на рис. 2.6. Рис. 2.5. К расчету ППЭ в области II. Сферические
составляющие напряженности электрического поля в подобласти II-а
имеют вид:
Последовательность
расчетов при использовании метода геометрической теории дифракции (ГТД)
следующая: 1. Определяется ряд вспомогательных величин:
φ1 = φ0 + ψ0 + θ; η1,2 = π - (φ1 sign η1,2 (sign η = 1, если η
≥ 1, sign η = -1, если η < 1);
Рис. 2.6. К расчету ППЭ методом ГТД. 2.
Вычисляются функции:
3.
Вычисляются специальные функции - интегралы Френеля:
в
которых
4.
Рассчитываются коэффициенты дифракции: D1 = m3 (Ф1m1 - Ф2m2);
D2 = m3 (Ф1m1 + Ф2m2) (2.32) 5.
Рассчитываются некоторые функции, определяющие дифракцию первичного поля
облучателя на кромке зеркала:
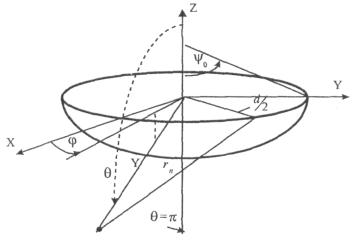
В
этих выражениях rn - расстояние от
произвольного элемента кромки ds до расчетной
точки:
r - расстояние от центра апертуры до
расчетной точки (рис. 2.6). 6.
Определяется усредненное значение ППЭ в центре апертуры:
7.
Определяется значение напряженности поля в центре апертуры: 8.
Рассчитываются сферические компоненты дифракционного поля Еθ,
Eφ по формулам:
где
α = 0,316 уровень поля на ребре кромки. 9.
Определяются составляющие ППЭ, обусловленные дифракционными компонентами поля Eθ, Eφ, по формулам: 10.
Если требуется найти декартовые составляющие дифракционного поля, то следует
воспользоваться следующими формулами: ЕХ = Eθ cos θ cos φ - Еφ sin φ; ЕY = Eθ cos θ sin φ + Еφ cos φ; ЕZ = -Eθ sin θ (2.39) В
секторе углов, принадлежащих подобласти II-б, значения сферических компонент дифракционного поля
определяется одной «светящейся» точкой (точка А на рис. 2.5) по формулам:
В
этих формулах: E0, определяется в
соответствии с (2.36), α = 0,316, коэффициенты дифракции
рассчитываются по формулам (2.28)...(2.32). Переход
к декартовым составляющим дифракционного поля осуществляется по формулам (2.39), а к сферическим компонентам
ППЭ по формулам (2.38). В
секторе углов подобласти II-в следует
принять, что Пдиф = 0. Расчет
плотности потока энергии в области III. Если зеркало антенны длиннофокусное (ψ < 90°), то в области III ППЭ имеет две составляющие. Одна определяется излучением
облучателя, другая - дифракцией на части кромки: ПΣ = Побл + Пдиф (2.42) Составляющая
Побл, определяется по формуле (2.23) с последующим переходом к
мкВт/см2, а составляющая Пдиф также, как для подобласти II-б. В
случае короткофокусной антенны (ψ < 90°) в области III ППЭ имеет составляющие Пдиф и Па. Составляющая Пдиф рассчитывается так же, как для подобласти II-а - по формулам (2.28)...(2.38). Расчет
плотности потока энергии в области IV. В области IV ППЭ
определяется в основном составляющими Побл и Пдиф, поэтому
значение ППЭ в этой области формально определяется по формуле (2.42) с добавлением составляющей Па. При этом дифракционная составляющая поля
определяется так же, как это сделано в подобласти II-а
- по формулам (2.28)...(2.38). Расчет
плотности потока энергии в области V. В этой области
ППЭ следует определять следующим образом: ПΣ = Побл + Пдиф При
этом составляющая Па рассчитывается по формулам (2.25) и (2.26), после того как предварительно геометрически
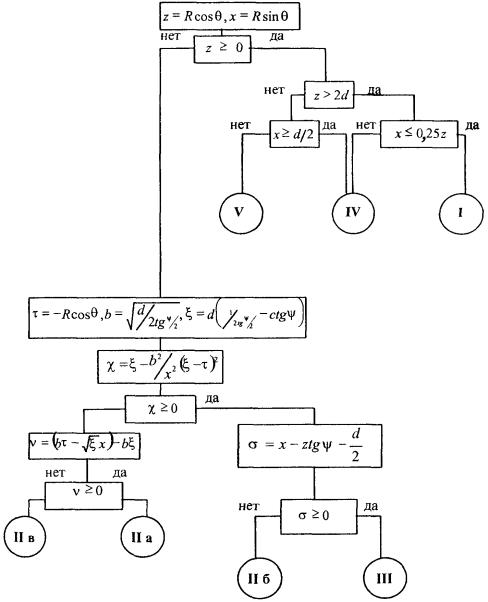
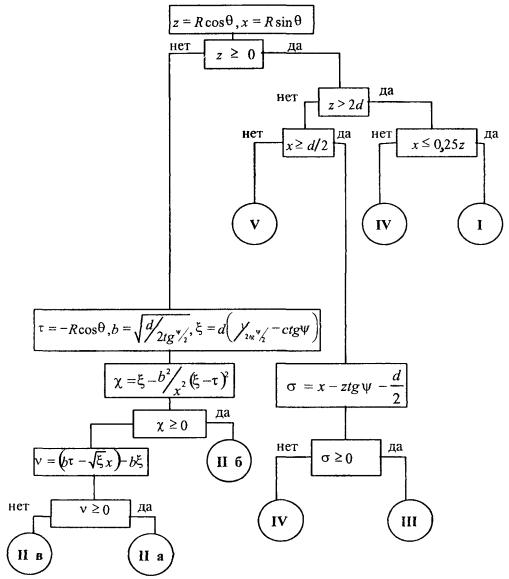
определена граница раздела между областями IV и V (значение Алгоритм
определения областей и подобластей для расчетной точки и примеры расчета ППЭ
приведены в приложении 2
- рис. П1.3 и П1.4. Примеры
расчета ППЭ вблизи параболических антенн с круглой апертурой приведены в
приложении 2. 3. Расчет плотности потока энергии вблизи параболических антенн с
квадратной и прямоугольной апертурой
Квадратная
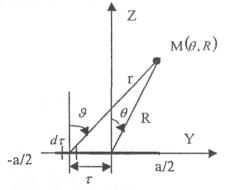
апертура. При анализе квадратной апертуры (рис. 3.1) используются допущения: -
распределение амплитуды поля в одной из главных плоскостей - «косинус на
пьедестале»: а - сторона
квадрата, τ - текущее значение
координаты апертуры в одной из главных плоскостей; · облучатель и
антенна имеют характеристики направленности с осевой симметрией относительно
направлений их максимального излучения; · значение
характеристики направленности облучателя вне сектора углов перехвата энергии
основным зеркалом равно 0,316 (по напряженности поля). Рис. 3.1. Квадратная апертура. Общая
расчетная формула для определения значения ППЭ имеет вид (2.1).
Физический смысл отдельных составляющих прежний. Составляющие Па и Побл
в децибелах относительно 1 мкВт/см2 будут иметь вид: Р - мощность,
излучаемая антенной, Вт; λ
- длина волны, м; а - сторона
квадрата (апертуры антенны), м; D0 - КНД антенны в
направлении максимального излучения в волновой зоне; В(х) -
функция, учитывающая изменение КНД квадратной апертуры в зависимости от
относительного расстояния; F(u ,x) - нормированная ХН квадратной апертуры в координатах и,
х; θ,
R - сферические координаты расчетной
точки; и =
(πa sin θ) / λ - обобщенная координата угла; х = R / Rгр - относительное расстояние; Rгр = 2а2 /
λ - граничное расстояние. Dобл - КНД
облучателя в направлении максимального излучения (величина безразмерная).
График зависимости Dобл,дБ = 10 lg Dобл как функции аргумента ψ0 для усредненной модели антенн приведен на рис. П1.2 (приложение 1). Вычисление
функции F(u, x) сводится к
расчету характеристики направленности линейного синфазного источника (рис. 3.2) с распределением амплитуды тока,
совпадающем с распределением амплитуды поля вида (3.1). Рис. 3.2. К расчету характеристики направленности. Значение
напряженности поля в расчетной точке определяется выражением: В (3.5) f(τ) определяется
распределением поля, а геометрические параметры υ, r являются функциями θ, R. Нормированная
характеристика направленности апертуры имеет вид: В
терминах обобщенных координат (и, х) направленные свойства апертуры
будут характеризоваться функцией F(u,
x). Функции
F(u, x) сильно осциллирующие, поэтому в практических расчетах ППЭ
следует использовать их гарантированные огибающие. Для удобства практических
расчетов гарантированные огибающие табулированы (приложение 3, таблицы 3.1
и 3.2). При значениях х
> 1, что соответствует дальней зоне, необходимо пользоваться
огибающими для х = 1. Аналитическое
выражение функции В(х)/х для квадратной апертуры с амплитудным
распределением типа «косинуса на пьедестале» имеет вид: где
В
области х ≤ 1 функция (3.7)
осциллирующая, а в области х
> 0,15 -
изменяется монотонно. При расчете ППЭ осциллирующую часть функции следует
заменить огибающей ее максимумов. На
рис. П3.1 (приложение 1) приведена функция 20 lg (B(x) / x). В области х > 1 функция 20 lg (B(x) / x) = -20 lg x. Порядок
расчета ППЭ в переднем полупространстве не отличается от приведенного для
круглой апертуры. Для
расчета ППЭ в области заднего полупространства вводится понятие
эквивалентной круглой апертуры. Диаметр эквивалентной апертуры определяется из
условия равенства площадей квадратной и круглой апертур:
Угол
раскрыва эквивалентной апертуры определяется по формуле: f - фокусное расстояние зеркала. Прямоугольная
апертура. Прямоугольная апертура со сторонами a и b показана на рис. 3.3. Рис. 3.3. Прямоугольная апертура. Расчетная формула для
апертурной составляющей ППЭ имеет вид: Функции
F(u,x), входящие в (3.13),
вычисляются в соответствии с (3.4)...(3.6) с учетом перехода к
обобщенным координатам и и x, а функции В(х)/х - по формуле (3.7) при х = х1 и х = х2,
соответственно. Расчет
составляющей ППЭ от облучателя выполняется по формуле (3.3). КНД облучателя следует
рассчитывать по формуле: D1 и D2 определяются по формулам (2.15) и (2.16) с учетом различных значений угла ψ0 в главных
плоскостях. Диаметр
эквивалентной круглой апертуры, необходимый для расчета дифракционной
составляющей ППЭ, определяется из условия равенства площадей прямоугольной и
круглой апертур:
Угол
раскрыва эквивалентной круглой апертуры определяется по формуле (3.12). Примеры
расчета ППЭ вблизи параболических антенн с квадратной и прямоугольной
апертурами приведены в приложении 3. 4. Расчет плотности потока энергии вблизи антенн типа
параболический цилиндр и рупорных антенн
Антенна
типа параболический цилиндр. Антенна имеет прямоугольную апертуру
(рис. 4.1). Распределение
амплитуды поля вдоль сторон апертуры в главных плоскостях XOZ и ZOY равномерное. Методика расчета ППЭ соответствует случаю
прямоугольной апертуры при f(τ) = const. Огибающие F(u, x) для случая f(τ) = const отличаются от
аналогичных кривых, соответствующих распределению (3.1)
не существенно (единицы дБ). Поэтому в практических расчетах можно использовать
данные, приведенные в табл. П3.1
и табл. П3.2. Значение
КНД облучателя рассчитывается по формуле: L - длина облучателя;
В
области заднего полупространства расчет ППЭ следует вести по формуле (3.3), приняв Dобл = D0. Рис. 4.1. Антенна типа параболический цилиндр. Пирамидальный
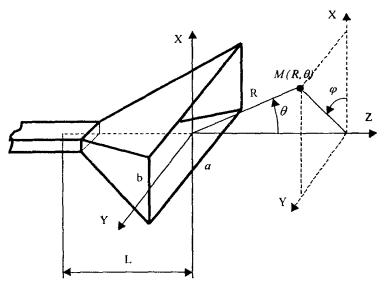
рупор. Пирамидальные (рис. 4.2)
и конические (рис. 4.3) рупорные
антенны имеют апертуры с неравномерным и несинфазным возбуждением. Линейные
размеры апертур обычно измеряются единицами, реже десятками длин
воли Расчетные точки, находящиеся на
расстоянии нескольких метров от таких антенн, относятся к дальней (волновой)
зоне. Плотность
потока энергии в переднем полупространстве вблизи таких антенн рассчитывается
по формуле: Р - мощность, изучаемая антенной, Вт; F(θ, φ) - характеристика направленности
рупора; Dp - КНД
рупора. Рис. 4.2. К расчету ППЭ
вблизи пирамидального рупора. Для
пирамидального рупора в расчетах следует принять: сомножители -
это нормированные характеристики направленности рупорной антенны
в E и H плоскостях. Для
расчета характеристики
направленности в плоскости Е (φ =
0) сначала вычисляется функция:
L, b - геометрические параметры рупора в Е плоскости; C(w1),
C(w2)
- косинусы интеграла Френеля S(w1),
S(w2)
- синусы интеграла Френеля Нормированная
характеристика направленности имеет вид: Для
расчета характеристики направленности в плоскости Н
L, а - геометрические
параметры рупора в Н плоскости; С(v1),
С(v2), С(v3), С(v4) - косинусы интеграла Френеля; S(v1), S(v2), S(v3), S(v4) - синусы
интеграла Френеля. Нормированная
характеристика направленности имеет вид: Значение
КНД пирамидальной рупорной антенны рассчитывается по формуле: С(u1),
С(u2), С(u3) - косинусы интеграла Френеля; S(u1), S(u2), S(u3) - синусы
интеграла Френеля. Конический
рупор. Для конического рупора функция F(θ, φ) рассчитывается
следующим образом. Сначала для заданного угла φ вычисляется
ненормированная характеристика направленности: f(θ) = q1 [U1(2γ,δ) + iU2(2γ,δ)] + q2J0(δ) + q3J1(δ), где (4.12)
Jm (l + 2n, δ)
- функция Бесселя порядка т = 1 + 2п
аргумента δ;
Jm (2 + 2n, δ) - функция Бесселя
порядка т = 2 + 2п аргумента δ; c1 = -0,37, c2 = -0,845, c3 = 0,215 - коэффициенты, соответствующие волне возбуждения H11 (при
равномерном возбуждении апертуры с1 = с2 = с3 = 0); J0(δ), J1(δ)
- функции Бесселя соответственно нулевого и первого порядка. Сходимость
рядов обеспечивается при п = 40. Нормированная
характеристика направленности имеет вид: Значение
КНД конической рупорной антенны рассчитывается по формуле: В
области заднего полупространства расчет ППЭ выполняется по формуле:
Рис. 4.3. К расчету ППЭ вблизи конического рупора. Примеры
расчетов ППЭ вблизи антенн типа параболический цилиндр, пирамидального и
конического рупора приведены в приложении 4. 5. Расчет плотности потока энергии вблизи
рупорно-параболической и перископической антенн
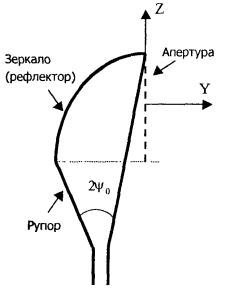
Конструкция
типовой рупорно-параболической антенны (РПА) схематично
представлена на рис. 5.1. Апертуру
можно считать квадратной с размером 2,7 × 2,7 м2. Методика
расчета ППЭ в переднем полупространстве (Y > 0) соответствует приведенной в разделе 3 для квадратной апертуры с
распределением амплитуды поля (3.1) - «косинус на пьедестале».
Составляющая Па рассчитывается
по формуле (3.2), составляющая По6л - по формуле (3.3).
При этом угол раскрыва рупора 2ψ0 = 35°. Учитывая, что РПА обладает хорошим защитным
действием (уровень бокового излучения исключительно низок: почти во всем
секторе углов он не превосходит -60...-70 дБ),
дифракционную доставляющую и составляющую По6л при расчете ППЭ в
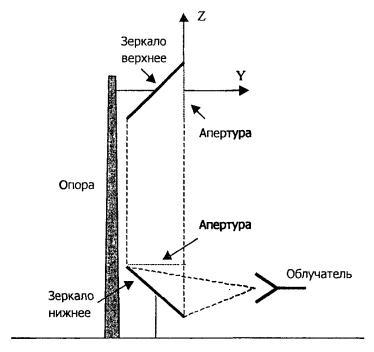
области заднего полупространства (Y < 0) не учитывать. Рис. 5.1. Рупорно-параболическая антенна. Перископические
антенные системы (ПАС) обычно строятся по трехэлементной схеме (рис. 5.2) - первичный рупорный облучатель,
нижнее зеркало и верхнее зеркало. Диаметр верхнего зеркала 3,9 м, нижнего 3,2
м. Диаметры апертур с учетом наклонного положения зеркал следует брать равными
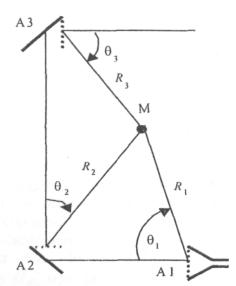
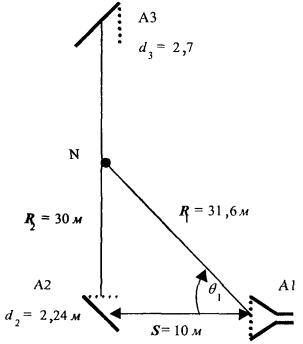
0,7 реальных диаметров зеркал. В
общем случае значение ППЭ в произвольной точке пространства M определяется тремя составляющими, каждая из которых
соответствует одной из трех антенн - Al, A2, A3 (рис. 5.3). Антенна
А1 рупорная. Её вклад в значение ППЭ определяется в
соответствии с методикой, изложенной в разделе 4. Антенны А2 и A3 имеют круглые апертуры. Их вклад в
значение ППЭ определяется апертурными
составляющими, которые рассчитываются по формуле (2.8). Вблизи
поверхности земли значение ППЭ определяется в основном антенной А1 -
облучателем, поэтому вклад апертурных составляющих верхнего и
нижнего зеркала можно не учитывать. Рис. 5.2. Перископическая антенная система. В
области Y < 0 следует ограничиться
только составляющей от антенны А1, то есть не учитывать составляющие ППЭ,
обусловленные дифракцией электромагнитных волн на зеркалах. Рис. 5.3. К расчету ППЭ
вблизи ПАС. Примеры
расчета ППЭ вблизи антенн РПА и ПАС приведены в приложении 5. 6. Учет влияния решетчатой структуры рефлектора
Решетчатая
структура рефлектора создает повышенный (по сравнению с зеркалом из сплошного
листа) уровень ППЭ в области заднего полупространства антенны. При облучении
рефлектора электромагнитной энергией происходит ее отражение (полезный эффект,
связанный с формированием диаграммы направленности антенны) и частичное
прохождение в область заднего полупространства (рис. 6.1). Рис. 6.1. Прохождение энергии через зеркало. Значение
составляющей Ппр в точке М, находящейся в области заднего
полупространства, определяется по формуле: Т - коэффициент
прохождения волны через решетчатую структуру (по полю); Р - мощность
излучения облучателя, Вт; Dобл - коэффициент
направленного действия облучателя (величина безразмерная); Fобл(γ)
- характеристика направленности облучателя (величина безразмерная); R - расстояние от фазового центра
облучателя до расчетной точки М, м. Угловая
зависимость коэффициента прохождения не учитывается. Значение T определяется для случая нормального падения плоской
волны на безграничную плоскую решетчатую структуру. Характеристика
направленности облучателя в области углов 0 < γ ≤ ψ0 имеет вид:
Значение
КНД облучателя рассчитывается по формуле (2.15). Для
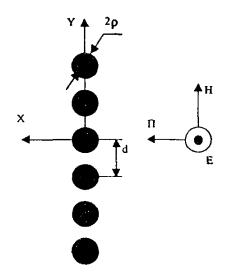
случая выполнения рефлектора (зеркала) из сетки линейных проводников (рис. 6.2) формула для расчета коэффициента
прохождения по полю имеет вид: H(2)0 (nkd), Н(2)0 (kρ) -
цилиндрические функции Бесселя 3-го рода (функции Ганкеля), k - волновое число для свободного пространства, d - расстояние между
проводами, ρ - радиус
проводов в сетке. Рис. 6.2. Падение плоской
волны на проволочную сетку. Функции
Бесселя рассчитываются по формулам:
Ряд,
стоящий в правой части (6.5), сходится достаточно
быстро (можно ограничиться десятью членами). В
случае выполнения отражательного зеркала в виде поверхности со щелями (рис. 6.3а) при длине щелей, отвечающих условию
(t > λ), считать, что полоски и щели имеют безграничную длину (рис. 6.3б). Для
практически важного случая d < (0,4...0,5)λ, формула расчета коэффициента прохождения
имеет вид:
Рис. 6.3. К расчету коэффициента прохождения через поверхность
со щелями. Для
поверхности с круглыми отверстиями (рис. 6.4) и расстоянии между центрами отверстий d
< (0,3...0,4)λ
формула для расчета коэффициента прохождения имеет вид:
d - расстояние между щелями, D - диаметр щели, t - толщина отражающей поверхности. В
тех случаях, когда геометрические параметры решетчатой структуры не позволяют
рассчитать коэффициент прохождения или структура решетки существенно отличается
от рассмотренных, следует брать Т = 0,01...0,02. Рис. 6.4. К расчету коэффициента прохождения через поверхность с
отверстиями. Пример
расчета ППЭ с учетом решетчатой структуры рефлектора приведен в приложении
6. 7. Расчет плотности потока энергии вблизи вибраторных антенн
Расчет
ППЭ вблизи вибраторных антенн осуществляется по формуле:
Вычислению
векторов напряженности электрического и магнитного полей предшествует решение
электродинамической задачи о нахождении функции распределения тока (токовой
функции) в проводниках антенны при заданном возбуждении. Данная
задача решается в приближении тонкого провода с использованием интегрального
уравнения Харрингтона. При этом используется метод коллокации
(метод сшивания в точках) при кусочно-синусоидальном базисе разложения токовой
функции. Антенна представляется системой цилиндрических проводников, радиус
которых не превышает 0,02λ.
Проводники разбиваются определенным образом на короткие отрезки (сегменты),
длина которых не превышает 0,1λ.
Соседние сегменты (на одном проводнике) частично перекрываются: начало
некоторого данного сегмента совпадает с центром предыдущего, конец - с центром
последующего. Интегральное
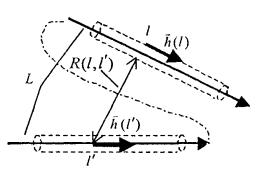
уравнение Харрингтона имеет вид: E0(l) - стороннее поле; L - контур, последовательно проходящий по
осям всех проводников - вдоль данного контура отсчитываются криволинейные
координаты l и l’ (см. рис. 7.1); ω - круговая частота; μ0 - магнитная постоянная; ε0 -
диэлектрическая постоянная;
a(l) - радиус проводника в
точке l; I(l’)
- искомая токовая функция. Рис. 7.1. К решению интегрального уравнения. Искомая
токовая функция I(l’)
при выбранном базисе разложения определяется как линейная комбинация: М -
число базисных функций, равное числу сегментов; Im - коэффициент
при m-ой базисной функции; Вm(l’) - m-ая кусочно-синусоидальная базисная функция. Представление
токовой функции в виде (7.3) сводит интегральное
уравнение (7.2) к системе М
линейных алгебраических уравнений относительно Im: k = 1, 2,...M, N - число входов (активных вибраторов)
антенны; I(вх)i - заданные
входные токи. Коэффициенты
системы (7.4) рассчитываются по формуле: lk и lm - средние точки
соответственно т-го и k-го сегментов; Lm - половина
длины т-го сегмента; R1, R0 и R2 - расстояния до средней точки k-го сегмента соответственно от начальной, средней и конечной точек
m-го сегмента;
Первые
М сегментов
вводятся собственно на проводниках антенны. Сегменты с номерами, превышающими M, вводятся в областях зазоров активных вибраторов, к
которым подводятся питающие напряжения (токи). Соответствующие им коэффициенты Zk,M+i,
обусловливающие неоднородность системы (7.4), также
рассчитываются по формуле (7.5). Найденные
коэффициенты Im, будучи
подставленными в (7.3), совместно с базисными
функциями восстанавливают функцию, аппроксимирующую распределение тока по
проводникам. Векторы
напряженности электрического и магнитного полей в заданной точке наблюдения с
радиус-вектором
Векторы
R1, R0 и R2 - расстояния
между точкой наблюдения и соответственно начальной, средней и конечной точками m-го сегмента;
При
т > М в формулах (7.7) и (7.8) в качестве коэффициентов Im, берутся соответствующие
заданные входные токи: Im = I(вх)m-N, т > N. Пример
расчета ППЭ вблизи вибраторной антенны приведен в приложении 7. 8. Учет
влияния подстилающей поверхности (земли, крыши)
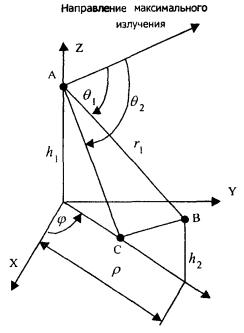
Учет
влияния плоской безграничной поверхности сводится к применению двухлучевой
модели (рис. 8.1). Рис. 8.1. Двухлучевая модель распространения радиоволн. В
точке В плотность потока энергии рассчитывается по формуле: П = П1 (θ1, φ1, r1) + П2
(θ2, φ2, r2), где (8.1) П1
(θ1, φ1, r1) - ППЭ,
создаваемая прямой волной (луч АВ); П2
(θ2, φ2, r2) -
ППЭ, создаваемая волной, распространяющейся по траектории АСВ;
Обе
составляющие рассчитываются по методике, соответствующей свободному
пространству. Для
учета влияния горизонтальной идеально проводящей плоскости конечных размеров
выделяется три области, соответствующие приближению геометрической оптики (рис.
8.2): I - область прямых лучей, II - область интерференции прямых и отраженных лучей, III - область тени, в которой предполагается отсутствие поля. Рис. 8.2. Деление пространства на области. Исходными
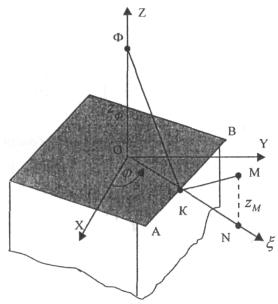
данными для учета конечных размеров крыши вдоль азимута φ (рис. 8.3) являются:
координаты фазового центра Ф{0, 0, zФ}, координаты расчетной
точки М{xM, yM, zm}, координаты углов крыши А{хA, уA, za}, В{хB, уB, zB]. Последовательность
расчета: 1. Вычисляются значения некоторых вспомогательных параметров: 2.
Определяются координаты точки К (точки пересечения кромки крыши АВ
линии Оξ): · для φ ≠ · для φ = xK = 0, yK = aAB (8.7) 3.
Рассчитываются расстояния: 4.
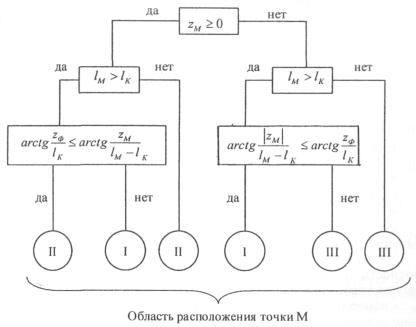
В соответствии с алгоритмом, приведенном на рис. 8.4, определяется принадлежность точки М к одной из трех
областей. 5.
Приведенный порядок расчета повторяется для всех выбранных значений φ, соответствующих положению линии Оξ,
внутри сектора углов АОВ. Рис. 8.3. К учету влияния горизонтальной крыши. Примечание. В приложении 9 приведена информация о рекомендуемом программном
обеспечении, включающем в себя расчеты плотности потока энергии по приведенным
выше методикам для рассмотренных технических средств. Рис. 8.4. Алгоритм
определения области нахождения точки М. 9. Инструментальный контроль уровней
электромагнитных полей радиосредств
9.1.
Инструментальный контроль уровней ЭМП проводится с целью определения
фактического состояния электромагнитной обстановки в местах расположения
излучающих радиосредств. Измерения
проводятся: · на этапе
предупредительного санитарного надзора (при приемке объекта в эксплуатацию); · на этапах
текущего санитарного надзора (при изменении ситуационных планов размещения
антенн, технических характеристик или режимов работы объекта; · после проведения
защитных мероприятий, направленных на снижение уровней ЭМП; · в порядке
плановых контрольных измерений (не реже одного раза в год). 9.2.
Подготовка к проведению инструментального контроля включает несколько этапов: · согласование
цели, времени и условий проведения измерений с заинтересованными организациями
и предприятиями; · рекогносцировку
района проведения измерений (подготовка информации о местности, рельефе,
наличии переотражающих поверхностей, выбор трасс и точек измерений); · подготовку
информации об источнике излучения (типы передающих средств, рабочие частоты,
режимы и мощности, типы антенн, их параметры и пространственное положение); · изучение
нормативной санитарно-гигиенической документации, относящейся к данному виду
технических средств; · обеспечение
измерений дальности до точки измерений; · подбор и
подготовку необходимой измерительной аппаратуры; · выполнение
расчетного прогнозирования; · определение
необходимости использования средств индивидуальной защиты. 9.3.
Для инструментального контроля используются измерители плотности потока энергии
(ППЭ), к которым предъявляются следующие требования: · измерительная
антенна (зонд, датчик поля) не должна существенно искажать структуру
измеряемого поля; · измерительная
антенна (зонд, датчик поля) должна иметь изотропную характеристику
направленности; · кабель,
соединяющий антенну с измерительным прибором не должен обладать антенным
эффектом; · частотный
диапазон измерительной антенны должен соответствовать диапазону частот
измеряемых электромагнитных полей; · прибор должен
обладать достаточной помехозащищенностью для работы в мощных мешающих ЭМП,
работать в стационарных и полевых условиях. 9.4.
Перечень рекомендуемых измерительных приборов приведен в таблице приложения. 9.5.
Выбор трасс (маршрутов) измерений. 9.5.1.
Число трасс определяется рельефом прилегающей местности и целью измерений. При
установлении границ СЗЗ выбирается несколько трасс, определяемых по
конфигурации теоретических границ СЗЗ и прилегающей селитебной зоны. При
текущем санитарном надзоре, когда характеристики объекта и условия его
эксплуатации остаются неизменными, измерения могут проводиться по одной
характерной трассе или по границе СЗЗ. 9.5.2.
При выборе трасс учитывается характер прилегающей местности (рельеф,
растительный покров, застройка и пр.), в соответствии с которым район,
прилегающий к объекту, разбивается на секторы. В каждом секторе выбирается
радиальная относительно объекта трасса. К трассе предъявляются требования: -
трасса должна быть открытой, а площадки, на которых намечается поведение
измерений, должны иметь прямую видимость на антенну излучающего средства; -
вдоль трассы, в пределах главного лепестка ХН, не должно быть
переизлучателей (металлических конструкций и сооружений, линий электропередачи
и т.п.) и других затеняющих местных предметов; -
наклон трассы должен быть минимальным по сравнению с наклоном всех возможных
трасс в данном секторе; -
трасса должна быть доступной для пешего передвижения или для автотранспорта; -
протяженность трассы определяется на основе расчетного удаления границ СЗЗ и
глубины зоны ограничения застройки (в 1,5-2 раза больше); -
точки (площадки) для проведения измерений следует выбирать с интервалом 5-10
м - при удалении до 100 м от излучающей антенны; 10-20 м - при удалении от 100
м до 300 м; 20-50 м - при удалении более 300
м. 9.6.
Проведение измерений. 9.6.1.
Выбор мест измерений определяется необходимостью по возможности исключить
облучение населения в местах его возможного
нахождения как в пределах санитарно-защитной зоны и зоны
ограничения, так и вне их. 9.6.2.
В обязательном порядке обследованию в границах санитарных зон подлежат здания
первой линии относительно объекта. В случае превышения предельно допустимого
уровня проверке подвергаются строения последующих линий, особенно строения,
высота которых превышает высоту строений первой линии. 9.6.4.
В каждой точке измерений следует находить максимальное значение ППЭ по высоте
до 2 метров. При этом следует руководствоваться требованиями п. 9.6.3. 9.6.5.
В каждой точке контроля производится три независимых измерения. Результатом
является максимальное значение этих измерений. 9.6.6.
По результатам измерений составляется протокол, который является неотъемлемой
частью санитарного паспорта. Приложение 1
Справочный материал для расчета ППЭ вблизи
параболической антенны с круглой апертурой
1.
Функция F(u, x) - круглая
апертура, u = 0...100 Таблица
П1.1
2. Функция F(u, x) - круглая
апертура и = 100...760 Таблица П1.2
3. Функция Рис. П1.1 4. Коэффициент направленного действия облучателя Рис. П1.2 5. Алгоритм
определения положения расчетной точки Рис. П1.3.
Случай длиннофокусной антенны ψ < π /
2. Рис. П1.4.
Случай короткофокусной антенны ψ < π /
2. Приложение 2
Примеры расчета ППЭ вблизи параболической антенны с
круглой апертурой
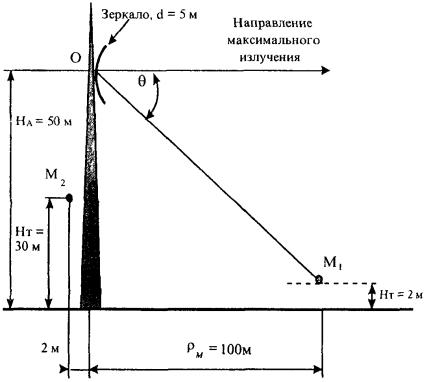
Пример 1 Исходные данные и постановка задачи Техническое
средство - оборудование РРСП ПВ «Радуга-4» на оконечной радиорелейной станции. Работают три
радиоствола. Мощность передатчика в каждом стволе 4 Вт. Используется антенна АДЭ-5 с диаметром антенны 5 м,
углом раскрыва зеркала 2ψ0 = 210°, КНД
43,5 дБ. Антенна находится на высоте 50 м. Частота - 3658,54 МГц. Сравнить
ППЭ в точках М1 и М2 с ПДУ ППЭ. Точка M1 расположена в направлении
на соседнюю станцию, ее высота над поверхностью земли - 2 м, а
удаление от основания мачты - 100 м Точка М2 расположена в азимутальном направлении 180° на расстоянии 2 м от оси мачты на высоте 30 м.
Постановка задачи иллюстрируется рис. П2.1. Рис. П2.1. Иллюстрация к примеру расчета ППЭ. Решение Расчет ППЭ в точке M1 1. По
алгоритму рис. П1.3
устанавливается принадлежность точки M1 к области IV. 2.
Находится расстояние RM - «центр апертуры - точка M1» и угол θM:
θM = arccos {[ρM · cos φ · cos α - (HA - HT) sin α] / RM} При φ
= 0 и α = 0: θM = arccos ρM / RM
= arcos 100 / 110,92 = 25,63° 3.
Находится граничное расстояние Rгр: Rгр = 2d2 /
λ = 2 · 52 / 0,082 = 609,76 м 4.
Определяются координаты х и и: x = RM / Rгр = 110,92
/ 609,76 = 0,182, и = (πd sin θM) / λ = (π · 5 · sin 25,63°) / 0,082 = 82,89 5.
По таблице П1.1 определяется
функция 20 lg F(u,
x) = -52,16 дБ 6.
По графику рис. П1.1 определяется
функция 20 lg [B(x) / x] = 13,22
дБ 7.
По формуле (2.8) рассчитывается
8.
По графику рис. П4.2 определяется
значение Dобл,дБ = 10 lg Dобл = 2,396 дБ 9.
По формуле (2.9) рассчитывается Побл = 10
1g (P / 4πR2М) + 10 lg Dобл + 10
= 10 lg [12 / (4π · 10,922)] + 2,396 + 10 = -28,7 дБ 10.
По формуле (2.24) рассчитывается
суммарная ППЭ в точке М1 без учета дифракционной
составляющей: П =
10ПА,дБ/10 + 10Побл,дБ/10
= 10-3,133 + 10-2,87 = 2,084 ·
10-3 мкВт/см2 11. Дифракционная составляющая ППЭ рассчитывается по формулам
(2.28)...(2.38), при этом: D1 = -0,0355 + i0,0323, D2 = 0,113 - i0,109, Eθ = 0,0255 - i0,0266, |Eθ| = 0,0368, |Eφ| = 0, Пθ = 3,602 × 10-4 12.
Рассчитывается суммарная ППЭ в точке M1 с учетом
дифракционной составляющей: П =
2,084 × 10-3 + 3,602 × 10-4 = 2,44 × 10-3 Вывод:
ППЭ в точке М1 меньше ПДУ
равного 10 мкВт/см2. Расчет ППЭ в
точке М2. 1.
Принимается, что
θ = 95,7106° 2.
По алгоритму рис. П1.4 устанавливается
принадлежность точки M2 к области IIб. Учитывая, что зеркало антенны короткофокусное 2ψ0 >
180°, поле в точке М2 будет
определяться только дифракционной составляющей. 3.
По формуле (2.41) рассчитывается Eθ = -7,256 × 10-2
+ i1,273 × 10-2.
При этом D2 =
0,114 - i0,107 (формулы (2.28)...(2.38)), Еθ = 18,827 (формула (2.36)). 4.
Определяется ППЭ в точке М2 по формуле (2.38): П =
1,44 × 10-3 мкВт/см2 Вывод:
ППЭ в точке М2 меньше ПДУ
равного 10 мкВт/см2. Исходные данные и постановка задачи Техническое
средство - ССП. Передатчик работает на длине волны λ = 0,05 м. Мощность передатчика Р = 3 кВт. Используется
антенна Кассегрена с углом раскрыва 2ψ0 = 180° и D0 = 50 дБ. Диаметр апертуры d =
7 м. Высота центра апертуры над землей НА = 7 м. Направление максимального излучения составляет с
плоскостью горизонта угол α = 10°.
Рассчитать ППЭ в точках М и N.
Исходные данные: НM = 2 м, φM = 5°, ρM = 300 м, HN = 4 м, φN =
160°, ρN = 20 м. Постановка
задачи иллюстрируется рис. П2.2. Рис. П2.2. Иллюстрации к примеру расчета ППЭ от
антенны ССП. Расчет ППЭ в точке М 1. Находится расстояние RM и угол
θM:
θM = arccos {[ρM × cos φM × cos α - (HA - HM) sin α] / RM} = = arccos {[300 × cos 5° × cos 10° - (7 - 2) sin 10°] / 300} = 12° 2.
По алгоритму рис. П1.3
устанавливается принадлежность точки М к области I. 3. Находится
граничное расстояние Rгр = 2d2 / λ = 2 × 72/0,05
= 1960 м 4.
Определяются координаты х и u в точке М: х = RM / Rгр = 300 / 1960 = 0,153, u = (πd sin θM) / λ = (π × 7 × sin 12°) / 0,05
= 91,4 5.
По графику рис. П1.1 определяется
функция 20 lg [B(x) / x] = 14
дБ 6.
По таблице П1.1 определяется
функция 20 lg F(u,
x) = -52,5 дБ 7.
По формуле (2.8) рассчитывается
8.
По графику рис. П.1.2
определяется Dобл,дБ = 10 lg Dобл = 3 дБ 9.
По формуле (2.9) рассчитывается Побл = 10
1g (P / 4πR2М) + 10 lg Dобл + 10
= 10 lg [3000 / (4π × 3002)] +
3 + 10 = -12,8 дБ 10.
По формуле (2.24) рассчитывается суммарная
ППЭ в точке М: П =
10ПА,дБ/10 + 10Побл,дБ/10
= 10-1,05 + 10-1,28 = 0,145
мкВт/см2 Вывод:
ППЭ в точке M меньше ПДУ равного 10
мкВт/см2. Расчет ППЭ в
точке N 2.1.
Находится расстояние RN и угол θN:
θN = arccos {[ρN · cos φN · cos α - (HA - HN) sin α] / RN} = = arccos {[20 ·
cos 120° · cos 10° - (7 - 4) sin 10°] / 20,224} = 160,2095° 2.2.
По алгоритму рис. П1.4
устанавливается принадлежность точки N к области II-а (рис. 2.5), где ППЭ имеет только дифракционную компоненту. 2.3.
Дифракционная компонента рассчитывается по формулам (2.28)...(2.38). Промежуточные результаты расчетов: D1 = 9,137 · 10-3 - i
· 9,077 · 10-3, D2 = 0,0347 - i · 0,0346, Eθ = 0,122
+ i · 0,0136, |Eθ| = 0,1228, Eφ
= 7,997 · 10-3 + i · 2,762 · 10-4 |Eφ| = 8,0 · 10-3, Пθ = 4,028 · 10-3 Окончательный
результат - значение ППЭ в точке N: П =
4,045 10-3 мкВт/см2. Исходные данные и постановка
задачи Рассчитать
ППЭ вблизи технического средства, рассмотренного в примере 2, если точка М (рис. П2.2) имеет координаты: φM = 0°, ρM = 3 м, HM = 7
м. Решение 1. Находится расстояние RM и угол
θM:
θM = arccos {[ρM · cos φM · cos α - (HA - HM) sin α] / RM}; θM = arccos
{[3 · cos 0° · cos 10° - (7 - 7) sin 10°] / 3} = 10° 2.
По алгоритму рис. П1.4
устанавливается принадлежность точки М к области V. 3. Находится
граничное расстояние Rгр = 2d2 / λ = 2 · 72/0,05 = 1960 м 4.
Определяется координата х в точке М: х = RM / Rгр = 3 / 1960 = 0,00153 5.
Определяется значение 6.
Определятся координата и: и = (π
- d sin θM) / λ = (π
7 sin 10°)
/ 0,05 = 76,37 7.
Вычисляется величина Пs по формуле (2.25): Пs = 400 Р / (πd20,65) = 400 · 3000 / (π · 72 · 0,65) = 11992,8 мкВт/см2 8.
Вычисляется апертурная составляющая ПА( -
по графику рис. П1.2 определяется
функция 20 lg [B(x) / x] = 14,5
дБ; - F(76,4;
0,00178) = 0; -
по формуле (2.8) рассчитывается ПА(
9. По
формуле (2.26) рассчитывается ПА(х,
и) для х = 0,00153:
10. По формуле (2.9)
рассчитывается Побл = 10
1g (P / 4πR2М) + 10 lg Dобл + 10
= 10 lg [3000 / (4π · 32)] +
3,2 + 10 = 27,437 дБ Побл = 540,93 11. Суммарное значение ППЭ в
точке М: П(х, и) = ПА(х, u) + Побл = 17174,72 Вывод:
ППЭ в точке N существенно превышает ПДУ, равный 10 мкВт/см2. Приложение 3
Справочные материалы и примеры расчета ППЭ вблизи
параболических антенн с квадратной и прямоугольной апертурами
1. Функция F(u, x) - квадратная
апертура, и = 0...100 Таблица П3.1
2. Функция F(u, x) - квадратная
апертура u = 100...760 Таблица П3.2
3. Функция Рис. П3.1 Пример 1. Антенна с квадратной апертурой Исходные данные и постановка задачи Техническое
средство - оборудование ТРРСП ТР-120 на оконечной станции.
Используются две несимметричных параболических антенны с размерами 30 ×
30 м2. Разнос между антеннами 40 м, центры апертур антенн находятся
на высоте НА = 25 м
над землей, мощность, излучаемая одной антенной Р = 5 кВт (при кпд АФТ
равном 1); длина волны λср = 0,3 м; КНД антенны D0,дБ = 47 дБ. Оценить
ППМ в точке М, которая расположена в направлении на
соседнюю станцию, а ее высота над землей - 2 м.
Удаление точки М от линии проекции антенн на поверхность земли 100 м.
Постановка задачи иллюстрируется рис. П3.2. Решение Расчет
ППЭ выполняется сначала для одной антенны затем для другой. Результаты расчетов
ППЭ суммируются. Расчет ППМ,
создаваемой антенной A1 в точке М 1. Находится расстояние RM и угол
θM:
θM = arccos {[ρM · cos φ · cos α - (HA - HТ) sin α] / RM} Для α = 0, φ = arcctg
(y/x) =
arcctg (20/100) = 11,31°, ρM = (z2
+ y2) = 102 м, θM = arсcos [(102 · cos 11,31°)
/ 104,5] = 16,95° 2.
Находится граничное расстояние Rгр = 2d2 / λ = 2 · 302/0,3 = 6000 м 3.
Определяются координаты х и и: х = RM / Rгр = 104,5 / 6000 = 0,01742, и = (πα sin θM) / λ = (π
· 30 · sin 16,95°) / 0,3 = 91,59. Рис. П3.2. Иллюстрации к примеру расчета ППЭ
от антенн ТРРСП. По
графику рис. П3.1 определяется
функция 20 lg [B(x) / x] = 13
дБ 5.
По таблице П3.1 определяется
функция 20 lg F(u,
x) = -29,6 дБ 6.
По формуле (3.2) рассчитывается
7. Угол
раскрыва зеркала антенны с размерами 30 × 30 м2
2ψ0 равен 40°.
По графику рис. П1.2 определяется Dобл,дБ = 10 lg Dобл = 9,53 дБ 8.
По формуле (3.3) рассчитывается Побл = 10
1g (P / 4πR2М) + 10 lg Dобл + 10
= = 10 lg [5000 / (4π · 104,542)] + 9,53 + 10 = 5,14 дБ 9.
По формуле (2.24) рассчитывается
ППЭ, создаваемая в точке М антенной А1 - П1: П1 =
10ПА,дБ/10 + 10Побл,дБ/10
= 100,084 + 100,514 = 4,53
мкВт/см2. Расчет ППМ, создаваемой антенной А2
в точке М 10.
В силу симметрии расположения точки М относительно антенн А1
и А2 ППЭ, создаваемая антенной А2 в точке M, будет равна ППЭ, создаваемой в этой точке антенной А1, т.е.
П1 = П2 =
4,53 мкВт/см2. 11. Суммарная ППЭ в точке М от совокупности антенн А1 и А2 и будет равна П = П1 + П2 = 4,53 + 4,53 9,06
мкВт/см2. Вывод:
ППЭ в точке М близка к ПДУ равному 10 мкВт/см2. Пример 2.
Антенна с прямоугольной апертурой Исходные данные и постановка задачи Антенна
выполнена в виде вырезки из параболоида вращения с прямоугольной апертурой
(рис. 3.3). Размеры апертуры а
= 2,7 м, b = 0,5 м. Мощность излучения 200
Вт, частота 10000 МГц. Угол раскрыва антенны в плоскости YOZ 2ψ1 = 180° в вертикальной плоскости ZOX ψ2 = 60°. Определить
значение ППЭ в точке М с координатами R = 48,6 м, θ = 5°. Решение 1. Определяются значения обобщенных координат по формулам (3.14): и1 = 24,64, х1 = 0,1, u2 = 4,56, х2 = 2,92. 2.
По таблице П3.1 находятся
значения гарантированных огибающих, следует учесть, что данные таблицы
приведены для функции 20 lg (F(u,x)): F(u1,x1) = -29,2, F(u2,x2) = -15,6 3.
Значение КНД облучателя рассчитывается по формуле (3.15), при этом частные значения КНД находятся по
графику рис. П1.2: D1 = 3,09 дБ, D2 = 8,96 дБ, D = 6,03 дБ 4.
Функции вида 10 lg (B(x) / x) находятся по графикам рис. П3.1 (следует
учесть, что графики построены для функции 20 lg (B(x) / x): 10
lg (B(x1) / x1)
= 6,5 дБ; 10 lg (B(x2) / x2)
= -4,65 дБ 5.
Подстановка исходных и найденных значений в формулу (3.13) дает апертурную составляющую ППЭ: Па = 2,38 дБ, Пa = 1,73 мкВт/см2 6.
Подстановка исходных данных и найденного значения КНД в формулу (3.3) позволяет найти составляющую ППЭ
от облучателя: Побл = -5,68 дБ, Побл = 0,2704
мкВт/см 7.
Суммарное значение ППЭ в точке М: П = 2,0 мкВт/см2 Пример 3 Исходные данные и постановка задачи Антенна
в виде вырезки из параболоида вращения (рис. П3.3) имеет квадратную апертуру со стороной квадрата 5
м. Угол раскрыва антенны ψ = 160°, рабочая частота 6 ГГц,
мощность 100 Вт. Определить
значение ППЭ в точке М, имеющей координаты X = 5 м, Y =
0, Z = -1 м. Рис. П3.3. Решение 1. Определяется значение диаметра эквивалентной круглой
апертуры по формуле (3.11): dэ = 5,642
м. 2.
Исходя из геометрии задачи определяются значения: R = 15,033, θ = 93,8°. 3.
По алгоритму рис. П1.3
устанавливается принадлежность точки М к области IIа, где учитываются одна составляющая ППЭ - дифракционная. 4.
Дифракционная составляющая ППЭ рассчитывается по формуле (2.41): Пдиф = 4,43
· 10-6 мкВт/см2 При
этом D2 = 1,613 · 10-3
- i1,609 · 10-3 (формулы (2.28)...(2.32)), Е0 = 48,166
(формула (2.36)), Еθ = -1,017
· 10-3 - i3,959 · 10-3 (формула (2.41)) 5.
Суммарная ППЭ в расчетной точке: П = 4,43 · 10-6 мкВт/см2. Приложение 4
Примеры
расчета ППЭ вблизи антенн типа параболический цилиндр и рупорных антенн
Пример 1. Антенна типа параболический цилиндр Исходные данные и постановка задачи Конструкция
антенны показана на рис. 4.1.
Размеры апертуры а = 0,45 м, b = 0,15 м. Длина излучателя L = 0,3 м. Мощность излучения 100 Вт, частота 10000 МГц,
КНД антенны 27 дБ. Определить
значение ППЭ в точке М с координатами R = 10 м, θ = 10°. Решение 1.
Определяются значения обобщенных координат по формулам (3.14): х1 = 0,741 и1
= 8,183, х2 = 6,667, u2 = 0,909. 2.
Нормированные характеристики направленности в обобщенных координатах и, х
рассчитываются по формулам (3.2)
и (3.3). Результаты расчетов
приведены на рис. П4.1 и П4.2. 3. Значения
огибающих функций определяются либо непосредственно по рис. П.3.1 и П.3.2,
либо, как это сделано ниже, по данным табл. П.3.1 (следует учесть, что данные таблицы приведены
для функции 20F(u, x): F(u1, x1)
= -10,5 дБ, F(u2, x2) =
-1,3 дБ Рис. П4.1. Функция F(u1, x1). Рис. П4.2. Функция F(u2, x2). 4.
Значение КНД облучателя рассчитывается по формуле (4.1): Si(kL) = 1,554, Dp = 20,4 5.
Находятся функции вида 10 lg(B(x) / x) по графикам рис. П3.1,
(следует учесть, что графики построены для функции 20 lg(B(x) / x): 10
lg(B(x1) / x1) = 6,3 дБ, 10
lg(B(x2) / x2) = -8,24 дБ 6.
Рассчитывается значение апертурной составляющей ППЭ по формуле (3.13): Пa = 16,6 мкВт/см2 7.
Считая облучатель синфазной нитью с равномерным возбуждением, определяется его
характеристика направленности облучателя:
8.
Подстановка исходных данных и найденного значения КНД в формулу (2.4) позволяет найти составляющую ППЭ
от облучателя: Побл = 3 мкВт/см2. Суммарное
значение ППЭ в точке М:П
= 19,6 мкВт/см2. Пример 2 Исходные данные и постановка задачи Пирамидальный
рупор, имеющий геометрические размеры (рис. 4.2) а = 28,5 см, b = 23,24 см, L = 90 см
возбуждается волной Н10 на частоте f = 10000 МГц. Подводимая мощность Р = 100 Вт.
Определить ППЭ в точке М с координатами R = 10 м, θ = 10°. Решение По
формуле (4.4)...(4.6) находим: f(10°) = 1,236, max f(θ = 0) = 3,5762 По
формулам (4.7)...(4.9) находим: f(10°) = 0,713, max f(θ = 0) = 2,779 По
формуле (4.3) определяем F(θ,φ) = 0,08868 Значение
КНД рупора определяем по формулам (4.10)
и (4.11): Dp = 475. Искомое
значение ППЭ находим по формуле (4.2): П = 0,2984 Вт/м2 = 29,84 мкВт/см2. Исходные данные и постановка задачи Конический
рупор, имеющий геометрические размеры (рис. 4.3) r = 15
см, L = 45 см возбуждается на частоте f = 10000 МГц. Подводимая мощность Р = 100
Вт. Определить ППЭ в точке М с координатами R = 9 м, θ = 10°. Решение По
формуле (4.13...4.19)
находим: q1 = 0,7158 + 0,1115i, q2
= 5,8658 · 102 - 0,9488i, f(θ = 10°) = 0,6957, max f(θ) = 0,8622, F(θ) = 0,6511 Значение
КНД рупора определяем по формул (4.20): Dp = 500. Искомое
значение ППЭ находим по формуле (4.2): П = 31,9811 Вт/м2 = 3198,11 мкВт/см2 Приложение 5
Примеры
расчета ППЭ вблизи рупорно-параболической и перископической антенн
Пример 1. Рупорно-параболическая антенна Исходные данные и постановка задачи Конструкция
антенны показана на рис. 5.1. Размеры
апертуры 2,7 × 2,7 м. Мощность излучения 2 Вт, длина волны λ = 8,2
см, КНД антенны 39,5 дБ. Угол раскрыва рупора ψ0 = 35°. Определить значение ППЭ в точке M, лежащей на оптической оси антенны (ось Y) на расстоянии R = 18
м. Решение 1. Находятся значения обобщенных координат и, х: u = 0, x = 0,101. 2.
По таблице П3.1 находится
значения гарантированной огибающей: F(u, x) = 0. 3.
Функции вида 10 lg(B(x) / x) находятся по
графикам рис. П3.1: 10
lg(B(x) / x) = 13,0 дБ 4.
Значение КНД облучателя находится по графику рис. П1.2: Do6л = 9,63 дБ 5.
Подстановка исходных и найденных значений в формулу (3.2) позволяет найти апертурную составляющую ППЭ: Пa = 19,532 дБ, Па = 89,78 мкВт/см2 6.
Подстановка исходных данных и найденного значения КНД в формулу (3.3) позволяет найти составляющую ППЭ
от облучателя: Побл = -13,45
дБ, По6л = 0,0452
мкВт/см2. Суммарное
значение ППЭ в точке М: П = 89,83 мкВт/см2. Пример 2.
Перископическая антенна Исходные данные и постановка задачи Конструкция
антенны показана на рис. 5.2.
Диаметр нижнего зеркала А2 - 3,2 м, верхнего зеркала A3 - 3,9 м. Расстояние
между верхним и нижним зеркалом 60 м, мощность излучения 2 Вт, длина волны λ
= 3,7 см, КНД антенны 43 дБ. Диаметр раскрыва конического рупора r = 0,15 м, длина L = 0,5 м. Определить значение ППЭ в точке M, находящейся на оси мачты на высоте 30 м. Расстояние между
рупором и мачтой 10 м. Постановка
задачи иллюстрируется на рис. П5.1. Решение В
точке N ППЭ имеет две составляющие - одну от нижней апертуры, другую от
верхней. Вклад
нижней апертуры (антенна А2) оценивается по формуле (3.21).
Результаты расчета: х =
0,111, и = 0,20 lg(B(x) / x) = 14,6 дБ, F(u,x) = 0, Пa = 28,7 дБ = 749 мкВт/см2. Рис. П5.1. Вклад
рупора (антенна А1) рассчитывается аналогично тому, как это сделано в примере 3 приложения 4. По
формуле (4.13)...(4.19) находим: q1 = -0,374 + 0,0631i, q2 = 0,017 - 0,37i, q3 = 0,712 + 0,033i U1(θ = 71,6°) = 0,113, U2(θ = 71,6°) = -1,929 · 10-4, f(θ = 71,6°) = 0,072, тах f(θ = 8°) =
1,215, F(θ = 71,6°) = 0,059 Значение
КНД рупора определяется по формуле (4.20): Dp = 328,7 Искомое
значение вклада рупора в ППЭ
находим по формуле (4.2): П = 1,955
Вт/м2, П = 195,5 мкВт/см2 Суммарное
значение ППЭ в точке N: П
= 944,5 мкВт/см2. Приложение 6
Пример расчета
ППЭ вблизи апертурной антенны с решетчатым рефлектором
Пример. Антенна с рефлектором в виде поверхности с отверстиями Исходные данные и постановка задачи Техническое
средство - ССП. Передатчик работает на длине волны λ = 0,05 м.
Мощность передатчика Р = 3 кВт. Используется антенна Кассегрена с углом
раскрыва 2ψ0 = 180° и D0 = 50 дБ. Зеркало (рефлектор) антенны -
параболоид вращения, поверхность которого выполнена в виде сетки из проводов
диаметра 2ρ = 0,006 м при расстоянии между проводами d = 0,018 м (рис. 6.2). Диаметр апертуры d = 7 м. Высота центра апертуры над землей НА = 7 м.
Направление максимального излучения составляет с плоскостью горизонта угол α
= 10°. Рассчитать ППЭ в точке N при: HN = 4 м, φN
= 160°, ρN = 20 м. Постановка задачи иллюстрируется рис. П2.2. Решение Параметры
технического средства и координаты точки N совпадают с заданными в
примере 3, приложения 2, поэтому значение дифракционной
составляющей считается известным и равным: Пдиф = 4,045 · 10-3 мкВт/см2 Значение
составляющей, обусловленной прохождением энергии сквозь сетку рефлектора, определяется
по формуле (6.1): 1. Находится
угол γ = 180° - θN = 180° - 160,24° = 19,76° 2.
Рассчитывается значение нормированной характеристики облучателя в точке N
(формула (6.2)):
Fобл = 0,973 3.
По графику рис. П1.1 определяется
КНД облучателя: Dобл = 3,095 дБ = 2,039 4.
Определяется коэффициент прохождения по формуле (6.3) H0(2)(kρ) = 1 + i · 0,695, при этом Т
= 0,028. 5.
По формуле (6.1) рассчитывается составляющая
ППЭ, обусловленная прохождением энергии через рефлектор: Ппр = 0,095 мкВт/см2 6.
Суммарная ППЭ в расчетной точке: П = 0,099 мкВт/см2 Приложение 7
Примеры расчета ППЭ вблизи вибраторных антенн
Пример 1. Коллинеарная
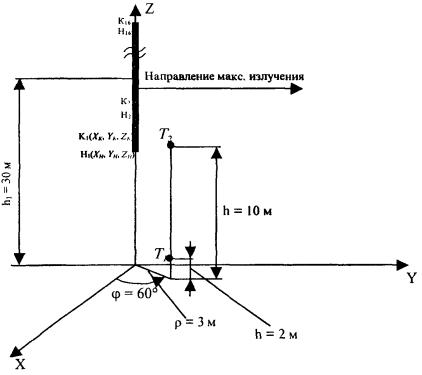
антенна, расположенная над плоской безграничной поверхностью Исходные данные и постановка задачи Техническое
средство - коллинеарная антенна базовой станции системы MMDS (вибраторы полуволновые), количество этажей - 16, питание
этажей - синфазное, рабочая частота f = 2400 МГц, излучаемая мощность Р = 800 Вт, высота подвеса
антенны h1 = 27 м. Рассчитать
уровни ППЭ в точках Т1 и Т2. Точка Т1
имеет следующие координаты в цилиндрической системе координат, связанной с
антенной: ρ = 3 м, φ = 60°, z = 2 м, а точка T2: ρ = 3 м, φ = 60°, z = 10 м. Антенна расположена над плоской
безграничной поверхностью. Постановка задачи проиллюстрирована на рис. П7.1. Рис. П7.1. Остальные
условные обозначения, использующиеся при расчетах, введены в соответствии с
параграфом 8. Решение Геометрия
антенны определяется исходя из следующих параметров: длины волны и высоты
подвеса антенны. λ = с / f =
3 · 108 / 340
· 106 =
0,125 м h1 = 30 м Далее
в декартовой системе координат с выбранным началом отсчета определяются
координаты начал и концов вибраторов в составе антенны. В таблице 1 приведены координаты только первого
этажа. Таблица 1
Радиусы вибраторов и число сегментов на вибраторах выбираются в
соответствии с требованиями, указанными в разделе 7. При
расчетах учитывается число этажей, межэтажное расстояние и высота подвеса
антенны. Режим возбуждения этажей - синфазный. 2.
Расчет координат точки наблюдения. Координаты
точки наблюдения, в которой вычисляется величины ППЭ, определяются в сферической системе координат наборами
величин θ1, φ, r1 и θ2,
φ, r2 (см. рис. 8.1).
В рассматриваемом случае при h2 = 2 м
Величина
φ была определена нами ранее и равна 60°.
При h2 = 10 м
3.
Расчет ППЭ. Расчет
напряженности поля производится в соответствии с методикой, подробно изложенной
в разделе 7. Исходными данными для
расчета являются введенная в пункте 1
геометрия антенны, а также режим возбуждения вибраторов и излучаемая мощность. Значение
ППЭ в точке Т1, рассчитанное по формуле (7.1), с учетом полученных выше результатов равно
1,0 · 10-3 мкВт/см2, а в точке T2 равно 4,4 · 10-2 мкВт/см2. Пример 2. Коллинеарная
антенна, расположенная на крыше высотного здания Исходные данные и постановка задачи Техническое
средство - коллинеарная антенна (вибраторы полуволновые), количество
этажей - 16, питание этажей - синфазное, рабочая частота f = 2400 МГц, излучаемая мощность Р =
800 Вт, высота подвеса антенны относительно уровня крыши (фазового центра): 5
м. Рассчитать
уровни ППЭ в точках М1 и М2. Точка M1 имеет следующие
координаты в декартовой системе: х = 5,77 м, у = 10 м, z = 4 м, а точка M2: х
= 6,78 м, у = 11,73 м, z = 1 м. Антенна расположена на крыше высотного здания
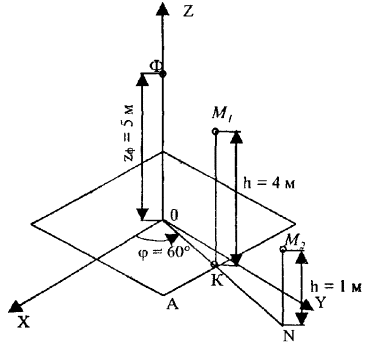
высотой 30 м. Координаты углов крыши A(5, 10, 30), В(-5, 10, 30). Координаты фазового центра Ф(0, 0, 5). Постановка задачи проиллюстрирована на рис. П7.2. Остальные
условные обозначения, использующиеся при расчетах, введены в соответствии с
разделом 8. Решение 1.
По формулам (8.5) вычисляются
значения вспомогательных параметров
Рис. П7.2.
2.
Расчет координат точки К. В соответствии
с выбранными параметрами задачи при φ = 60° для
расчета используются формулы (8.6).
3.
По формулам (8.8) рассчитываются
расстояния:
4.
В соответствии с алгоритмом, приведенном на рис. 8.4, определяется принадлежность точек М1
и М2 к одной из трех областей. Суть этого алгоритма состоит в
проверке нескольких условий. Так, для точки М1: zМ1 = 4 ≥ 0, lМ1 = lK Для
точки М2: zМ2 = 1 ≥ 0, lМ2 = lK,
Таким
образом, точка М1 находится в
области II, а точка M2 - в области I. 5.
Геометрия антенны. Геометрия
антенны определяется исходя из следующих параметров,
длины волны и высоты подвеса фазового центра антенны
относительно крыши. λ = c / f = 3 · 108 /
2400 · 106 = 0,125 м; h1 = 5 м Далее
в декартовой системе координат с выбранным началом отсчета определяются
координаты начал и концов вибраторов (аналогично примеру 1) в составе антенны с учетом высоты подвеса фазового
центра антенны. 6.
Расчет координат точки наблюдения. Координаты
точки наблюдения, в которой вычисляется величины ППЭ, определяются в
сферической системе координат наборами величин θ1, φ, r1 и θ2, φ, r2 (см. рис. 8.1). В отличие от результатов, приведенных в примере 1, число наборов координат определяется
в зависимости от номера области. Так, для точки M1, находящейся в области II, ППЭ определяется суммой ППЭ прямой и отраженной волны.
Поэтому для этой точки рассчитывается набор параметров, аналогичный
рассмотренному в примере 1: θ1 = 4,948°, φ = 60°, r1 = 11,59
м, θ2 = 37,926°, φ = 60°, r2 = 14,64 м Точка
M2 находится в области
прямых лучей. Поэтому для нее рассчитывается следующий набор параметров: θ1 =
16,45°, φ = 60°, r1 = 14,13 м 7.
Расчет ППЭ. Расчет
напряженности поля производится в соответствии с методикой, изложенной в
разделе 7. Исходными данными для
расчета являются введенная в 2.1
геометрия антенны, а также режим возбуждения вибраторов и излучаемая мощность. Значение
ППЭ в точке М1, рассчитанное
по формуле (7.1), с учетом
полученных выше результатов равно 14,82 мкВт/см2, а в точке M2 равно 0,187
мкВт/см2. Приложение 8
Перечень приборов, рекомендуемых для измерения ППЭ
Таблица П8.1
Могут быть использованы также другие приборы с аналогичными
характеристиками, приведенными в данной таблице. Приложение 9
Рекомендуемое
программное обеспечение
Программная
реализация приведенных в настоящих методических указаниях методик расчета
плотности потока энергии электромагнитного поля в местах размещения
радиосредств, работающих в диапазоне частот 300 МГц-300
ГГц, осуществлена в Программном комплексе анализа электромагнитной обстановки
(ПК АЭМО версия 2.0.2), разработанном специалистами ФГУП СОНИИР совместно с ЗАО
«СМАРТС». На данный программный комплекс имеется Свидетельство № 1002/02-00006 от 15 октября 2002 г., выданное Министерством
здравоохранения Российской Федерации, согласно которому ПК АЭМО пригоден к
использованию в учреждениях госсанэпидслужбы Российской Федерации. За
более подробной информацией о возможностях данного программного комплекса
обращаться по адресу: 443011, г. Самара,
ул. Советской Армии, 217, т. (8462) 16-18-26, факс (8462) 16-15-11, E-mail: mspd@soniir.samara.ru, fdv@soniir.samara.ru. Приложение 10
Список сокращений
ППЭ
- плотность потока энергии КНД
- коэффициент направленного действия ГТД - геометрическая теория дифракции РПА
- рупорно-параболическая антенна ПАС
- перископическая антенная система | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|