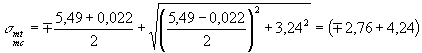|
ПОСОБИЕ
(к СНиП 2.03.01-84) ЧАСТЬ II Утверждено Москва Рекомендовано к
изданию решением секции несущих конструкций научно-технического совета
ЦНИИпромзданий Госстроя СССР. Пособие состоит из двух
частей, издаваемых отдельными книгами. Часть I. Разд. 1. Общие
указания. Разд. 2.
Материалы для железобетонных конструкций. Разд. 3.
Расчет элементов железобетонных конструкций по предельным состояниям первой
группы. Часть II. Разд. 4. Расчет элементов железобетонных конструкций по
предельным состоянием второй группы. Разд. 5. Конструктивные требования. Содержит требования СНиП 2.03.01-84,
относящиеся к проектированию указанных конструкций, положения, детализирующие
эти требования, приближенные способы расчета, дополнительные указания,
необходимые для проектирования, а также примеры расчета. Для
инженерно-технических работников проектных организаций, а также студентов
строительных вузов. При
пользовании Пособием следует учитывать утвержденные изменения строительных норм и правил и государственных стандартов, публикуемые в журнале «Бюллетень строительной техники», «Сборнике изменений к строительным
нормам и правилам» Госстроя СССР и информационном указателе «Государственные
стандарты СССР» Госстандарта. 4. РАСЧЕТ ЭЛЕМЕНТОВ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ВТОРОЙ ГРУППЫРАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО ОБРАЗОВАНИЮ ТРЕЩИН4.1 (4.1). Железобетонные элементы
рассчитываются по образованию трещин: нормальных к
продольной оси элемента; наклонных к
продольной оси элемента. Расчет по
образованию трещин производится: а) с целью
избежать их появления: в элементах, к
трещиностойкости которых предъявляются требования 1-й категории; в элементах, к
трещиностойкости которых предъявляются требования 2-й категории, если по расчету
не обеспечивается надежное закрытие этих трещин; на концевых
участках элемента в пределах длины зоны передачи напряжений арматуры без
анкеров lр (см. п. 2.26); б) для
определения необходимости проверки по раскрытию трещин (2-я и 3-я категории
трещиностойкости) и по закрытию трещин (2-я категория трещиностойкости); в) для выяснения
случая расчета по деформациям. Нагрузки,
коэффициенты надежности по нагрузке gf и коэффициенты точности
натяжения gsp, применяемые при расчете по
образованию трещин, приведены в табл. 2. Для участков
элемента в пределах зоны передачи напряжений следует учитывать снижение
предварительного напряжения ssp (s¢sp) согласно п. 1.20. Примечание. При расчете элементов по предельным состояниям первой группы также может потребоваться расчет по образованию трещин в случаях, указанных в пп. 1.13, 3.30, 3.58 и 3.59. Расчет по образованию трещин, нормальных к продольной оси элемента4.2 (4.5, 4.7). Расчет железобетонных
элементов по образованию нормальных трещин производится из условия Mr £ Mcrc, (163) где Mr - момент внешних сил,
расположенных по одну сторону от рассматриваемого сечения, относительно оси,
параллельной нулевой линии и проходящей через ядровую точку, наиболее удаленную
от растянутой зоны, трещинообразование которой проверяется; Mcrc - момент, воспринимаемый
нормальным сечением при образовании трещин и определяемый по формуле Mcrc = Rbt,ser Wpl ± Mrp, (164) здесь Mrp - момент усилия Р относительно той же оси, что и для
определения Mr, равный: Mrp = P (e0p ± r). (165) В формулах (164) и
(165)
знак «плюс» принимается, когда направления действия моментов Mr и Mrp противоположны (т.е. усилие
Р сжимает растянутую зону (черт. 38),
«минус» - когда эти направления совпадают (см. черт. 40). Значение Мr определяется по формулам: для изгибаемых
элементов (черт. 38, а) Mr = M; для внецентренно
сжатых элементов (черт. 38, б) Mr = N (e0 - r); (166) для внецентренно
растянутых элементов (черт. 38, в) Mr = N (e0 + r). (167) r - расстояние от центра
тяжести приведенного сечения до ядровой точки, наиболее удаленной от растянутой
зоны, трещинообразование которой проверяется. Значение r
определяется для элементов: внецентренно
сжатых и изгибаемых, а также для внецентренно растянутых при N £ Р по формуле где j = 1,6 - sb/Rb,ser, но не менее 0,7 и не более
единицы [sb
- максимальное напряжение в сжатом бетоне от внешней нагрузки и усилия
предварительного напряжения, вычисляемое как для упругого тела по приведенному
сечению (см. п. 1.21)]; Wred - момент сопротивления
приведенного сечения для крайнего растянутого волокна, определяемый как для
упругого тела по формуле Wred = Ired /y0, (169) у0 - расстояние от центра
тяжести приведенного сечения до растянутой грани; внецентренно
растянутых при N > P по формуле где Wpl - момент сопротивления приведенного сечения для крайнего растянутого
волокна с учетом неупругих деформаций растянутого бетона, определяемый в
предположении отсутствия продольной силы N и усилия предварительного обжатия Р
согласно п. 4.3.
Черт. 38. Схема усилий и эпюра напряжений в поперечном
сечении элемента при расчете его по образованию трещин, нормальных к продольной
оси элемента, в зоне сечения, сжатой от действия усилия предварительного обжатия а - при изгибе; б - при внецентренном сжатии; в - при внецентренном растяжении; 1 - ядровая точка; 2 - центр тяжести приведенного сечения Для стыковых
сечений составных и блочных конструкций, выполняемых без применения клея в
швах, при расчете их по образованию трещин (началу раскрытия швов) значение Rbt,ser в формуле (164) принимается равным нулю. Для
центрально-обжатых элементов при центральном растяжении их силой N (т.е. при е0 = е0р = 0) условие (163)
принимает вид N £ Rbt,ser (A + 2aAsp,tot + 2aAs,tot) + P, (171) где Asp,tot, As,tot - соответственно площадь
всей напрягаемой и ненапрягаемой арматуры. 4.3. (4.7). Значение Wpl определяется по формуле
где Ib0, Is0, I¢s0
- моменты инерции соответственно площадей сечения сжатой зоны бетона, арматуры S и S¢ относительно нулевой линии; Sb0 - статический момент
площади сечения растянутой зоны бетона относительно нулевой линии. Положение
нулевой линии в общем случае определяется из условия где S¢b0,
Ss0, S¢s0
- статические моменты соответственно площадей сечения сжатой зоны бетона,
арматуры S и S¢ относительно нулевой линии; Abt - площадь сечения
растянутой зоны бетона. Для
прямоугольных, тавровых и двутавровых сечений условие (173) принимает вид где
Формулой (174) не
следует пользоваться, если нулевая линия пересекает сжатые или растянутые
свесы. Допускается
значение Wpl определять по формуле Wpl = g Wred, (175) где Wred - см. п. 4.2; g - см. табл. 38. Таблица 38
Примечание. Обозначения bf и hf соответствуют размерам полки, которая при расчете по образованию трещин является растянутой, а b¢f и h¢f - размерам полки, которая для этого случая является сжатой; Wpl = g Wred. 4.4. При расчете по образованию
трещин в стадиях транспортирования, возведения и эксплуатации значение Mcrc определяется по формулам: а) если сила Р2 сжимает растянутую зону б) если сила Р2 растягивает эту зону
(например, вблизи опор неразрезанных балок)
rsup, rinf - расстояние от центра
тяжести приведенного сечения до ядровых точек, наиболее удаленных
соответственно от стороны, сжатой усилием Р2,
и стороны, растянутой этим усилием, определенные согласно п. 4.2
(черт. 39). Если вычисленное
по формуле (177)
значение Mcrc отрицательно, то это
означает, что трещине образованы до приложения внешней нагрузки. При расчете по
подпункту «а» на участках элемента с начальными трещинами в сжатой зоне
(см. п. 4.5)
значение Mcrc необходимо снижать согласно
указаниям п. 4.6. Черт. 39. Определение величин rsup и rinf а - при расчете по образованию трещин в зоне сечения, сжатой от действия усилия предварительного обжатия; б - то же, в зоне сечения, растянутой от действия усилия предварительного обжатия; 1 - ядровая точка; 2 - центр тяжести приведенного сечения; 3 - точка приложения усилия предварительного обжатия Для вычисления Mr в формулах (166) и
(167)
принимаются значения r,
равные rsup и rinf, т.е. такие же, как и при
определении Mcrc. 4.5. Расчет по образованию
начальных трещин в зоне сечения, растянутой от действия усилия предварительного
обжатия (черт. 40) в стадии изготовления, производится из условия где Mr - момент внешних сил,
действующих на элемент в стадии изготовления (например, от собственного веса),
принимаемый согласно п. 4.2; знак «плюс» принимается, когда направления
этого момента и момента усилия Р1
совпадают, знак «минус» - когда направления противоположны;
Черт. 40. Схема усилий и
эпюра напряжений в поперечном сечении элемента при расчете его по образованию
трещин, нормальных к продольной оси элемента, в зоне сечения, растянутой от
действия усилия предварительного обжатия 1 - центр тяжести приведенного сечения; 2 - ядровая точка 4.6. (4.6). При расчете по образованию
трещин на участках элемента с начальными трещинами в сжатой зоне [т.е. там, где не выполняется условие (178)] значение Mcrc для зоны, растянутой от внешней нагрузки, определенное по формуле (176), необходимо снижать путем
умножения на коэффициент q, равный: и принимаемый не более
единицы. В формуле (179): где где у0 - расстояние от центра
тяжести приведенного сечения до крайнего волокна бетона, растянутого внешней
нагрузкой. Усилие Р1 в формуле (180)
определяется при том же коэффициенте gsp, что и усилие Р2,
вводимое в расчет по п. 4.4а. Для конструкций,
армированных проволочной арматурой и стержневой арматурой класса А-VI,
значение d, полученное по формуле (181)
(без учета ограничения), снижается на 15 %. 4.7 (4.8). В конструкциях, армированных
предварительно напряженными элементами (например, брусками), при определении
усилий, воспринимаемых сечениями при образовании трещин в предварительно
напряженных элементах, площадь сечения растянутой зоны бетона, не подвергаемая
предварительному напряжению, в расчете не учитывается. 4.8 (4.10). Расчет по образованию трещин при действии
многократно повторяющейся нагрузки производится из условия sbt £ Rbt,ser, (182) где sbt - максимальное нормальное
растягивающее напряжение в бетоне, определяемое в соответствии с указаниями пп.
1.21 и 3.58. Расчетное
сопротивление бетона растяжению Rbt,ser в формуле (182)
вводится с коэффициентом условий работы gb1 по табл. 35. Расчет по образованию трещин, наклонных к
продольной оси элемента
4.9 (4.11). Расчет по образованию трещин, наклонных к продольной оси элемента,
должен производится из условия smt £ gb4 Rbt,ser, (183) где gb4 - коэффициент условий
работы бетона, определяемый по формуле здесь ab - коэффициент, принимаемый
равным для бетона: тяжелого 0,01 мелкозернистого и легкого 0,02 В -
класс бетона по прочности на сжатие, МПа; значение ab В следует принимать не менее
0,3. Для тяжелого
бетона при smc < 0,5Rb,ser и В £ 30 МПа можно, не пользуясь
формулой (184),
принимать gb4 = 1,0. Значения главных
растягивающих и главных сжимающих напряжений в бетоне smt и smc определяется
по формуле где sх - нормальное напряжение в бетоне на площадке,
перпендикулярной продольной оси элемента, от внешней нагрузки и усилия
предварительного обжатия Р,
определенное по п. 1.21; при этом sх принимается равным
напряжению в бетоне sb; sу - нормальное напряжение в
бетоне на площадке, параллельной продольной оси элемента, от местного действия
опорных реакций, сосредоточенных сил и распределенной нагрузки (см. п. 4.10), а
также от усилия обжатия вследствие предварительного напряжения хомутов и
отогнутых стержней (см. п. 4.11); tху - касательное напряжение в
бетоне от внешней нагрузки и усилия обжатия вследствие предварительного
напряжения отогнутых стержней (см. п. 4.12). Проверка условия
(183)
производится в центре тяжести приведенного сечения, а при требованиях к
трещиностойкости 1-й и 2-й категорий также и в местах примыкания сжатых полок к
стенке элемента таврового и двутаврового сечений. При расчете
элементов с предварительно напряженной арматурой без анкеров должно учитываться
снижение предварительного напряжения ssp и s¢sp на длине зоны передачи
напряжения lp (см. п. 2.26) путем
умножения на коэффициент gs5 согласно поз. 3 табл. 23. Примечание. В случае необходимости напряжения sх и tху от внешней нагрузки и предварительного обжатия алгебраически суммируются с напряжениями sх,loc и tloc от местного действия опорных реакций и сосредоточенных сил, равных:
где jx, jxy - определяются по табл. 39; F - см. п. 4.10. Таблица 39
Примечания: 1. Положительные значения jx и jy соответствуют сжимающим напряжениям sx и sy, отрицательные значения - растягивающим напряжениям; при положительных значениях jxy напряжение tloc имеет то же направление, что и txy, определенное по п. 4.12, при отрицательных - противоположное. 2. a и b - см. п. 4.10.
4.10. Значение sy, подставляемое в формулу (185), принимается равным сумме
напряжений от местного действия опорных реакций и сосредоточенных сил sy,loc и напряжений от усилия обжатия вследствие предварительного напряжения
хомутов и отогнутых стержней syp, определяемых согласно п. 4.11. Напряжения sy,loc определяется как для упругого тела по формуле где F -
величина сосредоточенной силы или опорной реакции;
Допускается sy,loc определять по формуле где jy - см. табл. 39. Положительные
значения sy,loc, вычисленные по формулам (186) и (187),
соответствуют сжимающим напряжениям, а отрицательные значения - растягивающим
напряжениям. При a > 0,7 напряжения sy,loc (а также sx,loc и tloc) принимаются равными нулю. 4.11. Значения сжимающих напряжений от усилия обжатия вследствие
предварительного напряжения хомутов и отгибов syp определяются по формуле
где Aspw - площадь сечения
напрягаемых хомутов, расположенных в одной плоскости, нормальной к оси
элемента; Asp,inc - площадь сечения напрягаемой отогнутой арматуры,
заканчивающейся на участке sinc длиной, равной h/2,
расположенном симметрично относительно рассматриваемого сечения 0 - 0 (черт. 41); sspw, ssp,inc - предварительное
напряжение соответственно в хомутах и в отогнутой арматуре; sw - шаг напрягаемых хомутов. Черт. 41. Криволинейная отогнутая напрягаемая арматура, учитываемая при
определении предварительных напряжений в бетоне: нормальных syp и касательных txy 1 - арматура, учитываемая при
определении напряжений txy в сечении 0 -
0; 2 - то же, напряжений syp на участке sinc 4.12. Касательные напряжения в бетоне txy следует определять по
формуле где Q - поперечная сила от
внешней нагрузки в рассматриваемом сечении; при этом следует учитывать
возможность отсутствия временной нагрузки на участке от опоры до
рассматриваемого сечения; Sred - приведенный статический
момент части сечения, расположенной выше рассматриваемого волокна, относительно
оси, проходящей через центр тяжести приведенного сечения; b - ширина сечения элемента
на уровне рассматриваемого волокна. В элементах с
напрягаемой отогнутой арматурой значение Q, подставляемое в формулу (189),
уменьшается на величину Qp = ssp Asp,inc1 sin q, (190) где Asp,inc1 - площадь сечения напрягаемой отогнутой арматуры,
заканчивающейся на опоре или на участке между опорой и сечением, расположенным
на расстоянии h/4 от рассматриваемого
сечения 0 - 0 (см. черт. 41); q - угол между осью арматуры
и продольной осью элемента в рассматриваемом сечении. При переменной
высоте балки значение поперечной силы для вычисления касательных напряжений
определяется по формуле где b - угол между сжатой и
растянутой гранями балки; Q1, М1 - поперечная сила и изгибающий момент (без учета
предварительного напряжения) в рассматриваемом поперечном сечении. В формуле (191)
знак «минус» принимается, если высота балки возрастает с увеличением
абсолютного значения изгибающего момента, и знак «плюс» - если высота убывает с
увеличением этого значения. Для элементов,
подвергающихся совместному действию изгиба и кручения, значение txy принимается равным сумме
касательных напряжений от изгиба, определяемых по формуле (189), и
от кручения tt. Значение tt определяют
по формулам пластического кручения, т.е. принимая, что к моменту образования
трещин эти напряжения имеют одинаковые значения по всему сечению элемента:
где Wt - момент сопротивления
сечения при пластическом кручении, равный Wt = 2V
[здесь V - объем тела, ограниченного
поверхностью равного ската с углом наклона 45° к плоскости сечения,
построенного на рассматриваемом сечении (черт. 42)]. Для элементов
прямоугольного сечения (черт.42, а)
значение tt равно: где h, b -
соответственно больший и меньший размеры сечения. Черт. 42. Схема определения
момента сопротивления при пластическом кручении для сечений а - прямоугольного; б - таврового 4.13 (4.12). При действии многократно
повторяющейся нагрузки расчет по образованию трещин должен производиться
согласно указаниям пп. 4.9 - 4.12; при этом расчетные сопротивления бетона Rbt,ser и Rb,ser вводятся в расчет с
коэффициентом условий работы gb1, принимаемым по табл. 35. Примеры расчетаПример 28. Дано:
элемент нижнего пояса фермы с размерами поперечного сечения 250 ´ 280 мм; бетон тяжелый
класса В35 (Rbt,ser = 1,95 Мпа,
Eb = 3,1 × 104 МПа);
продольная арматура: напрягаемая класса К-7 (Es = 18 × 104 МПа),
площадью сечения Asp = 1275 мм2 (25 Æ 9), ненапрягаемая класса А-III (Es = 2 × 105 МПа),
площадью сечения As,tot = 314 мм2 (4 Æ 10); предварительное
напряжение с учетом всех потерь ssp = 922 МПа; суммарные потери напряжения от усадки и
ползучести бетона ss = 201 МПа; усилие предварительного обжатия
приложено центрально; способ натяжения арматуры - механический; продольная
осевая растягивающая сила от всех нагрузок (при gf > 1,0) N =
1100 кН; требования к трещиностойкости 2-й категории. Требуется проверить элемент по образованию трещин. Расчет производим из условия (171). Так как к
трещиностойкости элемента предъявляется требование 2-й категории, учитываем
коэффициент точности натяжения gsp < 1. Согласно п. 1.18, при
механическом натяжении gsp = 1 - Dgsp = 1 - 0,1 = 0,9, т.е. ssp = 0,9 × 922 = 830 МПа. Определяем
усилие Р согласно п. 1.19. Для
центрально-обжатого элемента формула (8)
приобретает вид P = ssp Asp,tot - ss As,tot = 830 × 1275 - 201 × 314 = 995000 Н. Для напрягаемой
и ненапрягаемой арматуры значения
+ 2 × 6,45 × 314) + 995 × 103 = 1158 × 103 Н > N = 1100 кН, т.е. от действия всех
нагрузок трещины не образуются и, следовательно, расчета по закрытию трещин не
требуется. Пример 29. Дано: элемент нижнего пояса
фермы с размерами поперечного сечения 250 ´ 280 мм; бетон тяжелый класса В35 (Rbt,ser = 1,95 МПа, Eb = 3,1 × 104 МПа); напрягаемая симметричная арматура класса A-IV, площадью сечения Asp = A¢sp = 1232 мм2 (2 Æ 28) (Es = 1,9 × 104 МПа), момент инерции приведенного сечения Ired = 608,3 × 106 мм4; расстояние от центра тяжести сечения до
нижней грани y0 = 140 мм; усилие
предварительного обжатия с учетом всех потерь и коэффициента точности натяжения
gsp = 1,0 (требования к
трещиностойкости 3-й категории) Р =
650 кН; его эксцентриситет относительно центра тяжести приведенного сечения е0р = 0; продольная
осевая растягивающая сила от всех нагрузок N = 850 кН; изгибающий момент
от всех нагрузок М = 45 кН · м. Требуется проверить сечение по образованию трещин. Расчет. Эксцентриситет внешней
продольной силы относительно центра тяжести приведенного сечения равен:
Для проверки
условия (163)
определяем момент сопротивления Wpl с помощью коэффициента g по табл. 38. Для
этого вычисляем момент сопротивления Wred:
По табл. 38
находим g = 1,75 (так как элемент
прямоугольного сечения), и, следовательно, Wpl = g Wred = 1,75 × 4,35 × 106 = 7,61 × 106
мм3. Так как Р
= 650 кН < N = 850 кН, значение r
определяем по формуле (169), принимая
Момент усилия
предварительного обжатия относительно оси, проходящей через ядровую точку,
определяем по формуле (165): Mrp = P (e0p
+ r) = 650 × 103 × 76 = 49,4 × 106 Н · мм =
49,4 кН · м. Момент внешней
продольной силы относительно той же оси, согласно формуле (167),
равен: Mr = N
(e0 + r) = 850 × 103 (52,9 + 76) = 109,6 × 106 Н · мм. Проверяем
условие трещинообразования (163): Mcrc = Rbt,ser
Wpl + Mrp
= = 1,95 × 7,61 × 106 + 49,4 × 106 = 64,2 × 106 Н · мм < Mr = 109,6 × 106 Н · мм, т.е. от действия всех
нагрузок трещины образуются и требуется проверка их ширины раскрытия. Пример 30. Дано: многопустотная плита
перекрытия - по черт. 43; бетон легкий класса В15 (Rbt,ser = 1,15 МПа, Rb,ser = 11 МПа); передаточная прочность Rbp = 12,5 МПа Требуется проверить плиту по образованию трещин. Расчет. Определяем моменты
сопротивления относительно грани, растянутой от внешней нагрузки
Черт. 43. К примерам расчета
30 и 34 а - фактическое сечение плиты; б - эквивалентное сечение плиты Находим моменты
сопротивления Wpl по
формуле (175).
Для этого представляем сечение плиты в виде двутаврового сечения, заменив пустоты
прямоугольниками, эквивалентными по площади и моменту инерции. Ширина и высота
такого прямоугольника соответственно равны: А = 0,907D = 0,907 × 159 = 144,2 мм; В =
0,866D = 0,866 × 159 = 138 мм. Тогда из черт. 43 имеем: bf = b¢f = 3580 мм; b =
3580 - 18 × 144,2 = 984 мм;
Из табл. 38 для
двутаврового симметричного сечения при Отсюда
Поскольку в
плите располагается в основном только напрягаемая арматура, точка приложения
усилия обжатия во всех стадиях совпадает с центром тяжести арматуры, т.е. e0p = y0 - a = 107 - 30 = 77 мм.
Определяем ядровые расстояния rsup и rinf по формуле (168).
При действии внешней нагрузки в стадии эксплуатации максимальное напряжение в
сжатом бетоне (т.е. по верхней грани) равно:
Тогда j = 1,6 - При действии
усилия обжатия Р1 в стадии
изготовления максимальное напряжение в сжатом бетоне (т.е. по нижней грани)
равно:
= 1,7 + 0,95 = 2,65 МПа. При этом можно
видеть, что минимальное напряжение бетона в этой стадии, равное Согласно п. 4.2,
принимаем: Mr = M = 133,7 кН · м; Mrp = P2 (e0p + rsup)
= 636 × 103 (77 + 56,5) = 84,9 кН · м; Mcrc = Rbt,ser Wpl + Mrp = 1,15 ×
38,25 × 106 + 84,9 × 106
= = 128,9 × 106 Н · мм =
128,9 кН · м < Мr
= 133,7 кН · м, т.е. нижние трещины
образуются и, следовательно, расчет по раскрытию трещин необходим. Пример 31. Дано: плита перекрытия по
черт. 44; бетон тяжелый класса В25 (Rbt,ser = 1,6 МПа, Rbt,ser = 18,5 МПа, Eb = 2,7 × 104 МПа); передаточная прочность Rbp = 20 МПа ( Требуется определить момент трещинообразования Mcrc. Расчет. Предварительно определяем
моменты сопротивления и ядровые расстояния относительно грани, растянутой от
внешней нагрузки
Ядровые
расстояния rsup и rinf определяем по формуле (168). При действии
внешней нагрузки в стадии эксплуатации максимальное напряжение в сжатом бетоне
равно:
Тогда j = 1,6 - При действии
усилия обжатия Р1 в стадии изготовления максимальное
напряжение в сжатом бетоне равно:
Тогда j = 1,6 - Находим моменты
сопротивления
(ginf = 1,75 и gsup = 1,5 согласно табл. 38). Проверим образование верхних
начальных трещин согласно п. 4.5: Р1 (e0p - rinf) - Mw
= 230 × 103 (167 - 69,6) - 5,3 × 106 = = 17,1 × 106 Н · мм > т.е. верхние трещины
образуются и, следовательно, значение Мcrc определяем
с учетом коэффициента q, вычисляемого согласно п. 4.6:
Принимаем d = 1,4; тогда
Определяем момент
трещинообразования Mcrc согласно п. 4.4а:
= 1,6 × 5,7 × 106 + 150 × 103 (165 + 58,7)
= 42,7 × 106 Н · мм =
42,7 кН · м, а с учетом коэффициента q Mcrc = 0,724 × 42,7 = 31 кН · м. Пример 32. Дано:
плита перекрытия по черт. 44; бетон тяжелый класса В25 (Rb,ser = 18,5 МПа, Rbt,ser = 1,6 МПа, Eb = 2,7 × 104 МПа);
передаточная прочность бетона Rbp = 20 МПа; геометрические характеристики приведенного сечения: площадь Ared = 5,55 × 104 мм2,
расстояние от центра тяжести сечения до растянутой грани y0 = 220 мм, момент инерции Ired = 718 × 106 мм4,
расстояние от центра тяжести всей растянутой арматуры до растянутой грани а = 50 мм; напрягаемая арматура класса A-IV без
анкеров (Es = 1,9 × 105 МПа),
диаметром 25 мм; площадь сечения сжатой арматуры A¢s = 50,3 мм2 (1 Æ 8); усилие предварительного
обжатия (с учетом всех потерь и gsp = 1,0) Р2
= 150 кН; его эксцентриситет e0p = 165 мм; предварительное
напряжение (с учетом потерь по поз. 1 - 5 табл. 4) ssp1 = 475 МПа; поперечная сила от внешней нагрузки в
опорном сечении (при gf = 1,0) Qmax = 50 кН; требования к трещиностойкости 3-й категории. Требуется проверить, образуются ли наклонные трещины в
пределах длины зоны передачи напряжений, и установить необходимость расчета по
раскрытию наклонных трещин. Черт. 44. Предварительно напряженная плита перекрытия а - приопорный участок; б - поперечное сечение Расчет. Рассмотрим сечения у грани
опоры (сечение I - I) и на расстоянии lp от торца плиты (сечение II - II) - в обоих случаях проверку
производим в центре тяжести сечения (y0 = 220 мм). Определяем
значение Р2 в
рассматриваемых сечениях. Для этого по формуле (19) вычисляем длину зоны передачи
напряжений lp, имея в виду, что stp = sspI = 475 МПа;
(wp = 0,25 и lp = 10 - из табл. 24). Для сечения I - I lx = 200 мм; в этом сечении,
согласно п. 1.19,
Для сечения II - II lx = lp, следовательно, Определяем
нормальные напряжения sx на уровне центра тяжести сечения по формуле (10)
при y =
0 и Р = Р2:
Определяем касательные
напряжения txy по формуле (189).
Для этого вычисляем статический момент приведенной площади части сечения,
расположенной выше центра тяжести сечения, относительно оси, проходящей через
центр тяжести сечения:
В сечении I - I принимаем Q1 = Qmax = 50 кН. Сечение II - II отстоит от точки приложения
опорной реакции на расстоянии x = lp - 135 = 398 - 135 = 263 мм (см. черт. 44), следовательно, согласно п.
3.22, для этого сечения QII = Qmax - q1 x = 50 - 10,5 × 0,263 = 47,2 кН, где q1 = g + v/2 = 3,5 + 14/2 = 10,5 кН/м; g = 3,5 кН/м - постоянная
нагрузка; v = 14 кН/м - временная
нагрузка. Тогда
Поскольку
напрягаемая поперечная арматура отсутствует, syp = 0. Напряжения sy,loc от местного действия опорной реакции Qmax = F = 50 кН определяем по
формуле (187). Для сечения I - I: xI
= 200 - 135 = 65 мм (см. черт. 44); yI = y0 = 220 мм; aI = xI /h = 65/350 = 0,186 <
0,7; bI = yI /h = 220/350 = 0,63. Из табл. 39 имеем
jy = 0,45. Тогда
Для сечения II - II: xII
= 263 мм; aII
= 263/350 = 0,75 > 0,7, следовательно,
принимаем По формуле (185)
определяем главные растягивающие и главные сжимающие напряжения, принимая sy = sy,loc: Для сечения I - I:
Для сечения II - II:
Так как для обоих сечений smc < 0,5Rb,ser = 0,5 × 18,5 = 9,25 МПа и В < 30 МПа, принимаем gb4 = 1,0, т.е. gb4 Rbt,ser = 1,6 МПа. Проверяем
условие (183).
Так как для обоих сечений smt < gb4 Rbt,ser = 1,6 МПа, наклонные трещины в пределах длины зоны
передачи напряжений на уровне не выше уровня центра тяжести сечения не
образуются, следовательно, требование п. 1.11 выполнено. Поскольку в
более удаленных от опоры сечениях значение Q, а следовательно, txy и smt будут меньшими, чем в сечении II - II, то наклонные трещины на
уровне центра тяжести сечения нигде не образуются и, следовательно, расчет по
раскрытию наклонных трещин не производится. РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО РАСКРЫТИЮ ТРЕЩИН4.14 (4.13). Железобетонные элементы
рассчитываются по раскрытию трещин: нормальных к
продольной оси элемента; наклонных к
продольной оси элемента. Проверки ширины
раскрытия трещин не требуется, если, согласно расчету по пп. 4.1 - 4.13, в
рассматриваемом сечении трещины не образуются от действия нагрузок, указанных в
табл. 2. Для элементов, к
трещиностойкости которых предъявляются требования 3-й категории, расчет по
раскрытию трещин в общем случае производится два раза: на продолжительное и
непродолжительное раскрытие трещин (см. п. 1.10). Для изгибаемых элементов при
предельно допустимой ширине раскрытия трещин acrc1 = 0,4 мм и acrc2 = 0,3 мм (см. табл. 1б) расчет по раскрытию
нормальных трещин можно производить только один раз: при при где Mrp - см. п. 4.2; при
этом используется то же значение Р,
что и при расчете по раскрытию трещин. Расчет по раскрытию трещин, нормальных к продольной оси элемента4.15 (4.14). Ширину раскрытия трещин,
нормальных к продольной оси элемента, acrc, мм, следует определять по формуле где d - коэффициент, принимаемый равным для элементов:
изгибаемых, внецентренно сжатых и внецентренно растянутых при P ³ N - 1,0; центрально и
внецентренно растянутых при P < N - 1,2; jl - коэффициент, принимаемый равным при учете: кратковременных
нагрузок и непродолжительного действия постоянных и длительных нагрузок - 1,0; многократно
повторяющейся нагрузки, а также продолжительного действия постоянных и
длительных нагрузок для конструкций из бетона: тяжелого: естественной влажности.......................................................... jl = 1,6 - 15 в водонасыщенном состоянии.......................................................... 1,2 при попеременном водонасыщении и высушивании..................................................................................... 1,75 мелкозернистого, групп: А............................................................................................................. 1,75 Б............................................................................................................. 2,0 В............................................................................................................. 1,5 легкого........................................................................................................ 1,5 значения jl для мелкозернистого и
легкого бетонов в водонасыщенном состоянии умножают на 0,8, а при попеременном
водонасыщении и высушивании - на 1,2; h - коэффициент, принимаемый
равным для арматуры классов: А-III, A-IV, A-V, A-VI - 1,0; Bp-II, K-7, K-19 -
1,2; B-II - 1,4; ss - приращение напряжений в стержнях крайнего ряда
арматуры от действия внешней нагрузки, определяемое согласно указаниям п. 4.17;
hf - a - принимается не менее
нуля; если во
внецентренно растянутых элементах растягивающая сила Ntot = N - P расположена между центрами
тяжести арматуры S и S¢, то при определении d - диаметр растянутой
арматуры, мм; при различных диаметрах стержней значение d принимается равным:
d1, ..., dk - диаметры стержней
растянутой арматуры; n1, ..., nk - число стержней с
диаметром соответственно d1, ..., dk. В случае
применения попарно расположенных стержней при назначении диаметра d следует учитывать указания
п. 5.22.
Кроме того, следует учитывать указания п. 4.16. 4.16 (4.14). Ширина раскрытия трещин,
определенная согласно п. 4.15, корректируется в следующих случаях: а) если центр
тяжести сечения стержней крайнего ряда арматуры S изгибаемых, внецентренно сжатых и внецентренно растянутых при e0,tot ³ 0,8h0 элементов отстоит от
наиболее растянутого волокна на расстоянии а2
> 0,2h, значение acrc должно быть увеличено путем умножения на коэффициент dа, равный:
и принимаемый не более 3. Для элементов, армированных
стержневой арматурой периодического профиля, диаметр которого не менее 10 мм,
при толщине бокового защитного слоя бетона 15 мм и менее значение acrc, определенное по формуле (194),
уменьшается на 20 %; б) для
изгибаемых и внецентренно сжатых элементов из тяжелого и легкого бетонов при jb = jf jl1 (198) и принимаемый не более
единицы, где jf - коэффициент, учитывающий
уровень нагружения и равный: jl1 - коэффициент, учитывающий длительность действия
нагрузки и принимаемый равным при учете: кратковременных
нагрузок и непродолжительного действия постоянных и длительных нагрузок - 1,0; продолжительного
действия постоянных и длительных нагрузок
но не менее единицы; М0 - момент, при котором
растянутый бетон над трещинами практически выключается из работы, равный: М0 = Мcrc + ybh2 Rbt,ser, (201)
Если Mr > M0, коэффициент jb не вычисляется. Mr - момент, определяемый
согласно п. 4.2,
от полной нагрузки, включающей постоянную, длительную и кратковременную
нагрузки; Mcrc, Mrp - см. п. 4.2;
в) для элементов
статически неопределимых конструкций, а также для свободно опертых балок при l/h £ 7 и m £ 0,02 вблизи мест приложения
сосредоточенных сил и опорных реакций ширину раскрытия трещин acrc, вычисленную по формуле (194),
допускается уменьшать путем умножения на коэффициент jloc, учитывающий местные
особенности напряженного состояния в железобетонных изгибаемых конструкциях и
определяемый по формуле но не менее 0,8 и не более
1,0. В формуле (202): F -
сосредоточенная сила или опорная реакция; М - изгибающий момент в
нормальном сечении, проходящем через точку приложения силы F; а - расстояние от точки
приложения силы F до рассматриваемого
сечения, принимаемое в соответствии с черт. 45, но не более 0,3h; h, h0 - расстояние от грани
элемента, к которой приложена сила, соответственно до растянутой грани и до
растянутой арматуры; г) для элементов
из легкого бетона класса В7,5 значение acrc должно быть увеличено на 20 %. Черт. 45. Расположение расчетных сечений вблизи опорных реакций в
жестких узлах и сосредоточенных сил при расчете по раскрытию трещин I - I - расчетные сечения; а - г - расчетные сечения у жестких узлов; д - расчетные сечения у сосредоточенной силы, приложенной к сжатой грани; е - то же, приложенной к уширениям (полкам) элемента 4.17 (4.15). Приращение напряжений в
растянутой арматуре ss от действия внешней
нагрузки в стадии эксплуатации (включая стадии транспортирования и возведения)
определяется из условия равенства нулю суммы моментов внешних и внутренних
усилий относительно оси, проходящей через точку приложения равнодействующих
усилий в сжатой или менее растянутой зоне сечения. Значения ss вычисляются по формулам для
элементов: изгибаемых
(черт. 46,
а) внецентренно
сжатых (черт. 46,
б)
внецентренно
растянутых (черт. 46, в) если e0,tot = или если N < P2, для внецентренно
растянутых элементов при 0 £ e0,tot £ 0,8h0 (черт. 46, г) где zs = h0 - а¢ - расстояние между центрами
тяжести арматуры S и S¢. В формулах (206) и
(207)
знак «плюс» принимается при расположении силы N за пределами расстояния между арматурой S и S¢, знак «минус» - при
расположении силы N
между центрами тяжести арматуры S и S¢. Для
центрально-растянутых элементов, т.е. при e0,tot =
0; формула (207)
приобретает вид
где Asp,tot, As,tot - площади сечения всей
напрягаемой и ненапрягаемой арматуры. Черт. 46. Схема усилий и эпюры напряжений в поперечном сечении элемента
при расчете его по ширине раскрытия трещин, нормальных к продольной оси, в зоне
сечения, сжатой от действия усилия предварительного обжатия а - при изгибе; б - при внецентренном сжатии; в - при внецентреном растяжении и e0,tot ³ 0,8h0; г - то же, при e0,tot < 0,8h0; 1 - точка приложения равнодействующей усилий в сжатой или менее растянутой зоне; 2 - центр тяжести площади арматуры S; 3 - центр тяжести площади приведенного сечения z - расстояние от центра
тяжести площади сечения арматуры S до
точки приложения равнодействующей усилий в сжатой зоне сечения над трещиной,
определяемое согласно указаниям п. 4.31: при этом коэффициент v
принимается как при непродолжительном действии нагрузки, т.е. v = 0,45; допускается z принимать таким же, как и
при расчете по деформациям на те же нагрузки, если (A¢sp + A¢s)
/ (bh0) < 0,01. В случае, когда Mr < Mcrc (см. п. 4.2),
значение ss
находится по формуле
где scrc - приращение напряжений в арматуре при действии нагрузки,
соответствующей моменту образования трещин, определяемое по формулам (203) -
(207) и (209) с заменой M на Mcrc и N на Ncrc = N (Mcrc /Mr); Mrp - см. п.
4.2. В случаях, когда Mr > Mcrc и Р2 ³ 350 (Asp + As) (где 350 - в МПа), значение ss для изгибаемых и внецентренно сжатых элементов допускается определять
по формуле
где Ms = M + Pesp - для изгибаемых элементов; Ms = Nes + Pesp - для внецентренно сжатых
элементов; jcrc - определяется по табл. 40. При расположении
растянутой арматуры в несколько рядов по высоте сечения в изгибаемых,
внецентренно сжатых, а также внецентренно растянутых при e0,tot ³ 0,8h0 элементах напряжения ss, подсчитанные по формулам
настоящего пункта, должны умножаться на коэффициент dn, равный: где x = xh0; значение x определяется по формуле (232);
при этом коэффициент ν принимается всегда как при непродолжительном
действии нагрузки, т.е. ν = 0,45; для изгибаемых элементов
допускается принимать x = 0,5h0; а1, а2 - расстояние от центра тяжести сечения арматуры S соответственно всей и
крайнего ряда стержней до наиболее растянутого волокна бетона. Таблица 40
Для внецентрено растянутых
элементов при e0,tot < 0,8h0 и при расположении арматуры
в несколько рядов по высоте сечения напряжение ss допускается принимать равным a¢sbs, где sbs - напряжение на уровне
наиболее растянутого ряда арматуры от действия внешних сил и усилия обжатия Р, определенное как для упругого тела по
приведенному сечению, включающему в себя площадь сечения сжатой зоны бетона, а
также площадь сечения всей продольной арматуры, умноженной на коэффициент
приведения a¢ = Es / (0,9Eb); высоту сжатой зоны можно определять согласно п. 3.58, используя указанный коэффициент a. В этом случае при
определении коэффициента Чтобы избежать
неконтролируемого раскрытия трещин и обеспечить отсутствие заметных неупругих
деформаций арматуры, значения напряжений ss + ssp для напрягаемой арматуры и ss - ssb для ненапрягаемой арматуры не должны превышать
соответствующие значения Rs,ser. При этом для многорядной
арматуры напряжение ss определяется с учетом коэффициента dп, принимая крайний ряд стержней рассматриваемой
арматуры (напрягаемой или ненапрягаемой). Здесь ssb - сумма потерь предварительного напряжения от
усадки и ползучести бетона (см. поз. 6, 8 и 9 табл. 4). На участках
элементов, имеющих начальные трещины в сжатой зоне (см. п. 4.5),
величину усилия предварительного обжатия Р2,
а также напряжение ssp следует снижать путем умножения на коэффициент q (см. п. 4.6). Примечания: 1. Для статически определимых элементов при однорядном расположении напрягаемой арматуры и при As < Asp /4 значение ss + ssp заведомо меньше Rs,ser. 2. Если разность расчетных сопротивлений напрягаемой и ненапрягаемой арматуры не превышает предварительного напряжения ssp, определенного без учета потерь от усадки и ползучести бетона, то значение ss - ssb заведомо меньше Rs,ser. 4.18 (4.16). Ширину раскрытия начальных
трещин в зоне сечения, растянутой от действия усилия предварительного обжатия в
стадии изготовления, определяют по формуле (194), принимая где М - момент от собственного веса и других
нагрузок, действующих на элемент в стадии изготовления; в формуле (211) за
положительный момент принимается момент, растягивающий зону с начальными
трещинами; z - определяется согласно п. 4.31 для
стадии изготовления. Черт. 47. Определение ширины раскрытия трещин, нормальных к продольной
оси элемента, в стадии изготовления а - схема усилий и эпюры напряжений; б - расположение расчетного сечения (I - I) при а > lp; в - расположение расчетного сечения (I - I) при а < lp; 1 - центр тяжести арматуры S; 2 - точка приложения равнодействующей усилий в сжатой зоне; 3 - монтажная петля При этом
рассматриваются сечения с наиболее неблагоприятным совместным действием усилий Р1 и М: в месте
установки монтажной петли или в конце зоны передачи напряжений lp (черт. 47, б, в).
Если момент от собственного веса М
растягивает верхнюю грань (сечение I - I), его следует учитывать с
коэффициентом динамичности 1,4 (см. п. 1.9), в противном случае (сечение II - II) - без коэффициента
динамичности. В рассматриваемой стадии усилие Р1 и момент М
рассматриваются как действующие непродолжительно. Глубина
начальных трещин hcrc в сжатой зоне должна быть
не более 0,5h0. Значение hcrc определяется по формуле hcrc = h - (1,2 + jm) x h0. (212) Значение jm определяется согласно п. 4.6.
Значение x определяется по формуле (232),
рассматривая стадию изготовления. 4.19 (4.14). Для элементов, к
трещиностойкости которых предъявляются требования 2-й категории, ширина
раскрытия трещин определяется от суммарного непродолжительного действия
постоянных, длительных и кратковременных нагрузок при коэффициенте jl = jl1 = 1,0. Для элементов, к
трещиностойкости которых предъявляются требования 3-й категории, ширина
продолжительного раскрытия трещин определяется от действия постоянных и
длительных нагрузок при коэффициенте jl > 1,0. Ширина непродолжительного раскрытия
трещин определяется как сумма ширины продолжительного раскрытия от постоянных и
длительных нагрузок и приращения ширины раскрытия трещин от действия
кратковременных нагрузок при коэффициенте jl = 1,0, т.е. по формуле где acrc,l - ширина продолжительного раскрытия трещин от
действия постоянных и длительных нагрузок; jl > 1,0 - см. п. 4.15; если величина acrc,l определена с учетом формулы (198),
то коэффициент jl в формуле (213) заменяется произведением jl jl1 (jl1 - см. п. 4.16б); ssl, ss - определяются согласно п. 4.17
соответственно от постоянных и длительных нагрузок и от всех нагрузок. Расчет по раскрытию трещин, наклонных к продольной оси элемента4.20 (4.17). Ширина раскрытия трещин,
наклонных к продольной оси элементов, при армировании хомутами, нормальными к
продольной оси, должна определяться по формуле где jl - коэффициент, принимаемый
равным при учете: кратковременных
нагрузок и непродолжительного действия постоянных и длительных нагрузок - 1,00;
многократно повторяющейся нагрузки, а также продолжительного действия
постоянных и длительных нагрузок для конструкций из бетонов: тяжелого: естественной влажности.............................................................. 1,50 в водонасыщенном состоянии.................................................... 1,20 при попеременном водонасыщении и высушивании.................................................................................. 1,75 мелкозернистого и легкого.......................................... то же, что и в формуле (194); h - коэффициент, принимаемый
равным для поперечной арматуры классов: А-I - 1,3; А-II и А-III -
1,0; Вр-I - 1,2; mw - коэффициент насыщения элемента хомутами, равный:
dw - диаметр хомутов; ssw - напряжение в хомутах, определяемое по формуле (значение напряжения ssw не должно превышать Rs,ser). Здесь Qb1 - правая часть условия (93);
при этом коэффициент jb4 умножается на 0,8, а значения Rbt и Rb заменяются на Rbt,ser и Rb,ser; значение Rbt,ser принимается не более значения, соответствующего бетону
класса В30; Q - поперечная сила от
внешней нагрузки, расположенной по одну сторону от рассматриваемого наклонного
сечения, определяемая согласно п. 3.22. Расчет
производится для наиболее опасных наклонных сечений, определяемых согласно п.
3.30б. При определении
ширины непродолжительного и продолжительного раскрытия наклонных трещин должны
учитываться указания п. 4.19; при этом в формуле (213) коэффициент jl назначается согласно
настоящему пункту, а отношение ssl/ss заменяется отношением
напряжений sswl/ssw, определяемых по формуле (216)
соответственно от постоянных и длительных нагрузок и от всех нагрузок. Допускается
уменьшать величину acrc в 1,5 раза по сравнению с определенной по формуле (214),
если элемент армирован поперечными стержнями, нормальными к оси элемента, и
продольными стержнями того же диаметра с расстояниями по высоте сечения,
равными шагу поперечных стержней. Примеры расчетаПример 33. Дано:
элемент нижнего пояса фермы с размерами поперечного сечения: h = 280 мм, b = 250 мм, а =
а¢ = 40 мм; бетон тяжелый
класса В35 (Rb,ser = 25,5 МПа, Eb = 3,1 × 104 МПа); продольная
растягивающая сила от всех нагрузок N =
850 кН; момент от всех нагрузок М =
45 кН · м; продольная сила и момент от постоянных и длительных нагрузок равны: Nl = 820 кН и Ml = 30 кН · м;
предварительное напряжение в арматуре с учетом всех потерь ssp2 = 264 МПа; остальные данные
- по примеру 29. Требуется рассчитать элемент по раскрытию нормальных трещин. Расчет. Проверяем непродолжительное
и продолжительное раскрытие трещин. h0 = 280 - 40 = 240 мм. Определяем
эксцентриситеты внешней продольной силы N и равнодействующей Ntot относительно центра тяжести приведенного сечения:
Ntot = N - P2 = 850 - 650 = 200 кН >
0; Nl,tot = 820 - 650 = 170 кН
> 0. Поскольку e0p = 0,
Продолжительное
раскрытие трещин определяем по формуле (194). Так как e0l,tot < 0,8h0, приращение напряжения в арматуре
ss определяем по формуле (207): es = y0 - а - e0l = 140 - 40 - 36,6 = 63,4
мм; esp = y0 - а = 140 - 40 = 100 мм; zs = h0 - а¢ = 240 - 40 = 200 мм;
Ширину раскрытия
трещин аcrc находим по формуле (194). Для этого вычисляем
коэффициенты:
jl = 1,6 - 1,5 h = 1,0; d = 1,2 (поскольку N > P2). Отсюда
т.е. продолжительное
раскрытие трещин меньше предельно допустимого - аcrc,2 = 0,3 мм (см. табл. 1б). Непродолжительное
раскрытие трещин определяем по формуле (213), принимая аcrc,l =
0,136 мм, ssl = 191
МПа и jl = 1,3. Для определения
величины ss находим значение z согласно указаниям п. 4.31: es = y0 - а - e0 = 140 - 40 - 52,9 = 47,1 мм; Ms = P2 esp
- Nes = 650 × 103 × 100
- 850 × 103 ×
47,1 мм = = 25 × 106 Н · мм;
ma = 0,021 × 6,5 = 0,137; v = 0,45;
Так как x = 0,155 <
Так как jf = 0, формула (238)
принимает вид z = h0 (1 - 0,5x) = 240 (1 - 0,5 × 0,224) = 213 мм. Приращение
напряжений в арматуре определяем по формуле (206):
Поскольку ssp2 + ss = 264 + 257 = 521 МПа < Rs,ser = 590 МПа, отсутствие неупругих деформаций в
арматуре обеспечено.
что меньше предельного
допустимого значения acrc,1 = 0,4 мм. Пример 34. Дано:
многопустотная плита перекрытия - по черт. 43; бетон легкий класса В15,
марки по средней плотности D1600 (Eb = 13900 МПа); продольная арматура класса А-IV, площадью сечения Asp = 1539 мм2 (10 Æ 14); усилие
предварительного обжатия (с учетом всех потерь и gsp = 1,0) P =
636 кН; момент от всех нагрузок Mtot = 133,7 кН · м; момент от постоянных и длительных нагрузок Ml = 106,4 кН · м; требования
к трещиностойкости 3-й категории; остальные данные из примера 30. Требуется рассчитать плиту по раскрытию нормальных трещин. Расчет. h0 = h - a = 220 - 30 = 190 мм (см.
черт. 43). Из примера 30 имеем Mrp = 84,9 кН · м. Так как Поскольку Mr = Ml = 106,4 кН · м < Mcrc = 128,7 кН · м, приращение
напряжений ss определяем по формуле (208). Для этого определим значение ss,crc от действия момента Mcrc = 128,7 кН · м. Поскольку 350Asp = 350 × 1539 = 538650 Н < P2 = 636 кН, воспользуемся упрощенной формулой (209).
Из примера 30
имеем b¢f = bf = 3580 мм, b =
984 мм и h = h¢f
= 41 мм. Тогда
Поскольку As = 0, A¢s
= 0 и A¢sp = 0, Ms = M = 128,7 кН · м;
Находим
коэффициент jcrc. Для этого по табл. 40 принимаем ближайшие
табличные значения jf = 0,5 и ma = 0,1 и интерполируем
только по es,tot
/h0: при
Из формулы (208) имеем
Ширину
продолжительного раскрытия трещин определяем по формуле (194) п.
4.15.
Из этого пункта имеем: jl = 1,5; d = 1,0; h = 1,0; d = 14 мм;
Определим ширину
непродолжительного раскрытия трещин по формуле (213), принимая acrc,l = 0,056 мм и ssl = 52,9 МПа. Напряжение ss определим по формуле (209), приняв Ms = Mtot = 133,7 кН · м:
Из табл. 40 при jf = 0,5, ma = 0,1 и Тогда
что меньше предельно
допустимого значения acrc1
= 0,4 мм. Пример 35. Дано:
плита перекрытия по черт. 44; класс тяжелого бетона В25 (Eb = 2,7 × 104 МПа);
передаточная прочность Rbp = 20 МПа Требуется определить ширину раскрытия и глубину нормальных
трещин в стадии изготовления. Расчет. Из примера 31
известно, что в рассматриваемой стадии образуются верхние (начальные) трещины.
Рассмотрим сечение в месте закрепления монтажных петель на расстояние l1 = 1 м от торца плиты.
Момент в этом сечении от собственного веса плиты найдем как для консоли с
учетом коэффициента динамичности, равного при подъеме 1,4 (см. п. 1.9):
Находим
напряжение в арматуре ss, необходимое для вычисления ширины раскрытия трещин
по формуле (211).
Для этой цели вычисляем плечо z
согласно указаниям п. 4.31; в связи с этим определяем следующие
величины: h0 = 350 - 25 = 325 мм;
esp = e0p + (h - y0 - а) = 167 + (350 - 220 - 25) = 272 мм; Ms = P1 esp + Mw = 230 × 103 × 272 + 0,9 × 106 = 63,5 × 106 Н · мм;
Так как z < 0,97es,tot = 0,97 × 276,4 = 268 мм, оставляем z = 267 мм. Напряжение в
растянутой арматуре ss
определяем по формуле (211):
Для определения
величины acrc находим коэффициент
что меньше предельно
допустимого значения acrc = 0,4 мм. В этом же
сечении определим глубину верхних трещин согласно п. 4.18:
здесь hcrc = h - (1,2 + jm) x h0 = 350 - (1,2 + 0,50) 0,375 × 325 = 143 мм, т.е. меньше
0,5h = 0,5 × 350 = 175 мм. Пример 36. Дано:
плита перекрытия по черт. 44; класс тяжелого бетона В25 (Eb = 2,7 × 104 МПа, Rb,ser = 18,5 МПа); напрягаемая арматура класса A-IV (Es = 1,9 × 105 МПа),
площадью сечения Asp = 491 мм2 (1 Æ 25); ненапрягаемая арматура
растянутая и сжатая класса А-III, площадью сечения
соответственно As = 78,5 мм2 (1 Æ 10) и A¢s
= 50,3 мм2 (1 Æ 8); усилие предварительного
обжатия (с учетом всех потерь и gsp = 1,0) Р2 = 150
кН; его эксцентриситет e0p = 165 мм; предварительное
напряжение ssp2 = 332 МПа; максимальный
момент от всех нагрузок при gf = 1,0 Mtot = 66 кН · м, в том числе момент от постоянных и длительных нагрузок Ml = 60 кН · м; требование к
трещиностойкости 3-й категории. Требуется рассчитать плиту по раскрытию нормальных трещин в
стадии эксплуатации. Расчет. Из примера 31
известно, что в стадии изготовления в верхней зоне плиты образуются начальные
трещины; с учетом этих трещин Mcrc = 31 кН · м < Mtot = 66 кН · м. Следовательно, расчет по раскрытию нормальных трещин в
нижней зоне плиты необходим. В связи с
наличием начальных трещин уточняем значение Р2.
Согласно п. 4.17,
усилие Р2 снижается путем
умножения на коэффициент q = 0,724 (см. пример 31): Р2 = 150 × 0,724 = 108,6 кН. Тогда Mrp = P2 (e0p
+ rsup) = 108,6 × 103 (165 + 58,7)
= 24,3 × 106 Н · мм =
24,3 кН · м (rsup принято по примеру 31). Так как Расчет
производим согласно указаниям пп. 4.15 и 4.17. Для определения ширины
раскрытия трещин находим значение z согласно указаниям п. 4.31: Ms = M + P2 esp = 60 × 106 + 108,6 × 103 × 5 = 60,5 × 106 Н · мм, где esp = y - e0p - a = 220 - 165 -
50 = 5 мм;
Напряжение в
растянутой арматуре ss определяем по формуле (203):
Определяем
коэффициент dп для нижнего ряда арматуры
(ненапрягаемой) по формуле (210), принимая х = 0,292h0 = 0,292 × 300 = 87,6 мм:
Тогда ss = 182 × 1,12 = 204 МПа. Ширину раскрытия
трещин определяем по формуле (194). Для этого вычисляем значения
Коэффициент jl равен: jl = 1,6 - 15
что меньше предельно
допустимого значения acrc = 0,3 мм. В соответствии с примечанием
к п. 4.17 напряжения ss
+ ssp и ss - ssb от действия всех нагрузок не проверяем. Пример 37. Дано: балка покрытия - по
черт. 48; бетон тяжелый класса В30 (Rbt,ser = 1,8 МПа, Eb = 2,9 × 104 МПа, Rb,ser = 22 МПа); продольная
арматура из канатов класса К-7 (Es = 1,8 × 105 МПа), площадью сечения Asp = 725 мм2 (8 Æ 12) и A¢sp = 182 мм2 (2 Æ 12); усилие предварительного обжатия (с учетом всех потерь и gsp = 1,0) P2 = 580 кН; его эксцентриситет относительно центра тяжести приведенного
сечения e0p = 420 мм; момент усилия
обжатия Mrp = 434 кН · м; момент трещинообразования Mcrc = 620 кН · м; момент от
всех нагрузок Mtot = 725 кН · м; требования к трещиностойкости 2-й категории. Требуется рассчитать балку по раскрытию нормальных трещин. Расчет. Ширину непродолжительного
раскрытия нормальных трещин от действия момента M = Mtot определяем по формуле (194). Для этого находим
приращение напряжения в арматуре ss. Черт. 48. Поперечное сечение балки покрытия Значение z вычисляем согласно
указаниям п. 4.31: h0 = h - a = 1500 - 120 = 1380
мм;
Ms = M + P2 esp = 725 × 106 + 580 × 103 × 340 = 922 × 106 Н · мм (esp = y
- a - e0p = 880 -
120 - 420 = 340 мм);
Поскольку
арматура расположена в несколько рядов, определяем ss для нижнего ряда; по формуле (210)
находим коэффициент
Отсюда ss = 239 × 1,075 = 257 МПа. Для определения
значения acrc находим коэффициент
армирования
jl = 1,0; d = 1,0, для арматуры класса
К-7 - h = 1,2. Отсюда
т.е. ширина раскрытия трещин
больше предельно допустимой acrc1
= 0,2 мм (см. табл. 1б). Поскольку Mr = M
= 725 кН · м. Определим
момент, при котором растянутый бетон выключается из работы, по формуле (201).
Для этого вычислим
Тогда M0 = Mcrc + y b h2 Rbt,ser = = 620 × 106 + 0,473 × 80 × 15002 × 1,8 = 773 × 106 Н · мм > Mr = 725 кН · м. Поскольку расчет
ведется на непродолжительное действие нагрузок, jl1 = 1,0, и тогда
Уточненное значение acrc = 0,227 × 0,799 = 0,181 мм, что не
превышает предельно допустимого значения acrc1 = 0,2 мм. Пример 38. Дано: плита покрытия пролетом l = 5,85 м, сечением - по черт. 49; бетон легкий класса В20 (Rbt,ser = 1,4 МПа), марки по средней плотности D1800 (Eb = 17,3 × 103 МПа);
поперечная арматура на опоре в виде U-образной
сетки из проволоки класса Вр-I (Es = 17 × 104 МПа),
диаметром 4 мм (Asw = 25,1 мм2), с
шагом поперечных стержней s =
100 мм; геометрические характеристики приведенного сечения (для половины
сечения): площадь Ared = 60400 мм2,
момент инерции Ired = 556,5 × 106 мм4,
расстояние от центра тяжести до нижней грани y0 = 274 мм; момент образования трещин при gsp = 1,0 Mcrc = 17 кН · м; усилие обжатия
Р = 50 кН; нагрузка, приходящаяся на
одно ребро, q = 8,4 кН/м, в том числе
постоянная и длительная ql = 7,2 кН/м; снеговая нагрузка: полная s = 3 кН/м, длительная sl = 1,8 кН/м. Требуется рассчитать плиту по раскрытию наклонных трещин. Расчет. h0 = 300 - 35 = 265 мм (см. черт. 49). Поперечная сила
на опоре равна:
Черт. 49. К примеру расчета 38 1 - напрягаемый стержень; 2 - U-образная сетка Согласно п. 3.30б, определим значения Qb1 и Q. По формуле (96) вычисляем значение Qcrc, принимая Rbt = Rbt,ser = 1,4 МПа, b = 96,7 мм (см. черт. 49) и
По графику на черт. 18 при s = Тогда
Поскольку Qcrc = 37,8 кН > Qmax, за невыгоднейшее значение с
принимаем длину приопорного участка l1, где не образуются
нормальные трещины. При равномерно распределенной нагрузке значение l1 определяем из уравнения
откуда
Так как 2,5h0 = 2,5 × 265 = 662 мм < l1, значение Qb1 принимаем равным значению Qb,min, определяемому по формуле (95) при Rbt = 1,4 МПа, b = 87 мм (см. черт. 49), jb4 = 0,4 (см. табл. 29) и
Qb,min = Qb1
= jb4 (1 + jn) Rbt bh0 = 0,4 (1 + 0,155) 1,4 × 87 × 265 = 14900 Н. Расчетную
поперечную силу Q принимаем в поперечном
сечении на расстоянии с = 0,8 м от
опоры, учитывая разгружающее влияние постоянной и половины временной (снеговой)
нагрузки (см. п. 3.22): при действии
всех нагрузок Q = Qmax - q1 с =
24,57 - 6,9 × 0,8 = 19,05 кН, где q1 = q - s/2 = 8,4 - 3/2 = 6,9 кН/м; при действии
постоянных и длительных нагрузок
где q1l = ql - sl /2 = 7,2 - 1,8/2 = 6,3 кН/м. Определим по
формуле (216)
напряжение в хомутах при действии постоянных и длительных нагрузок:
Ширину
продолжительного раскрытия трещин от действия этих нагрузок определим по
формуле (214),
принимая jl = 1,5; h = 1,2; dw = 4 мм;
что меньше предельно
допустимого значения acrc2
= 0,3 мм (см. табл. 1б). Определим
напряжение ssw при действии всех нагрузок:
Ширину
непродолжительного раскрытия трещин определим по формуле (213),
принимая
что меньше предельно
допустимого значения acrc1
= 0,4 мм. РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО ЗАКРЫТИЮ ТРЕЩИН4.21 (4.18). Железобетонные элементы
должны рассчитываться по закрытию (зажатию) трещин: нормальных к
продольной оси элемента; наклонных к
продольной оси элемента. Расчет по
закрытию трещин производится для зон элементов (см. п. 1.10), к
трещиностойкости которых предъявляются требования 2-й категории, если в этих
зонах элементов трещины образуются от действия постоянных, длительных и
кратковременных нагрузок при коэффициенте надежности по нагрузке gf > 1,0. Расчет по закрытию трещин, нормальных к продольной оси элемента4.22 (4.19). Для обеспечения надежного
закрытия трещин, нормальных к продольной оси элемента, при действии постоянных
и длительных нагрузок должны соблюдаться следующие требования: а) в напрягаемой
арматуре S от действия постоянных,
длительных и кратковременных нагрузок не должны возникать необратимые
деформации, что обеспечивается соблюдением условия ssp + ss £ 0,8Rs,ser, (217) где ss - приращение напряжения в
напрягаемой арматуре S от
действия внешних нагрузок, определяемое согласно п. 4.17; при этом для
ненапрягаемой арматуры класса Вр-I также должно выполняться
условие (217)
с заменой ssp на - ssb (см. п. 4.17) б) сечение
элемента с трещинами в растянутой зоне от действия постоянных, длительных и
кратковременных нагрузок должно оставаться обжатым при действии постоянных и
длительных нагрузок с нормальными напряжениеми сжатия sb на растягиваемой внешними
нагрузками грани элемента не менее 0,5 МПа; при этом величина sb определяется как для
упругого тела от действия внешних нагрузок и усилия предварительного обжатия Р2; для изгибаемых элементов
данное требование соблюдается, если выполняется условие M £ P2 (e0p + r) - 0,5Wred, (218) где r - расстояние от центра
тяжести приведенного сечения до ядровой точки, наиболее удаленной от
растягиваемой внешними нагрузками грани элемента, определяемое по формуле
Wred - см. п. 4.2; 0,5 - требуемое напряжение
сжатия в МПа на растягиваемой внешними нагрузками грани элемента. Для внецентренно
сжатых и внецентренно растянутых элементов в условии (218) момент М заменяется значением Mr, определяемым согласно п. 4.2; при
этом r определяется по формуле (219). 4.23 (4.20). Для участков элементов,
имеющих начальные трещины в сжатой зоне (см. п. 4.5), величина ssp в условии (217)
умножается на коэффициент q, а величина Р2 в условии (218)
умножается на коэффициент, равный 1,1q, но не более 1,0, где
значения q определяются согласно
указаниям п. 4.6. Расчет по закрытию трещин, наклонных к продольной оси элемента4.24 (4.21). Для обеспечения надежного
закрытия трещин, наклонных к продольной оси элемента, оба главных напряжения в
бетоне, определяемые, согласно указаниям п. 4.9, на уровне центра тяжести
приведенного сечения при действии постоянных и длительных нагрузок, должны быть
сжимающими (т.е. значение smt должно быть отрицательным) и по величине не менее
0,5 МПа. Указанное
требование обеспечивается с помощью предварительно напряженной поперечной
арматуры (хомутов или отогнутых стержней). В этом случае требуемая величина
сжимающего напряжения в бетоне, вызванная влиянием предварительного напряжения
поперечной арматуры (см. п. 4.11), определяется по формуле где sx, txy, sy,loc - принимаются в МПа и
определяются, согласно пп. 4.9 - 4.12, на уровне центра тяжести
приведенного сечения; при этом напряжения txy и sy,loc определяются от действия
постоянных и длительных нагрузок. Формулу (220)
следует использовать при подборе поперечной напрягаемой арматуры лишь в том
случае, если при найденной по ней величине syp наклонные трещины образуются, т.е. при действии
постоянных, длительных и кратковременных нагрузок с gf > 1,0 не выполняется условие (183). В
противном случае значение syp может быть снижено таким образом, чтобы обеспечить
указанное условие. Примеры расчетаПример 39. Дано:
балка покрытия - по черт. 48; продольная арматура из канатов класса К-7 (Æ 12 мм) (Rs,ser = 1335 МПа); предварительное напряжение в арматуре S (при gsp = 1,0) ssp = 640 МПа; усилие предварительного обжатия (с
учетом всех потерь и gsp < 1,0) P2 = 520 кН; момент от постоянных и длительных
нагрузок Ml = 340 кН · м;
геометрические характеристики приведенного сечения: площадь Ared = 21 × 104 мм2,
момент сопротивления Wred = 69 × 106 мм3;
требования к трещиностойкости 2-й категории; остальные данные по примеру 37. Требуется рассчитать балку по закрытию нормальных трещин. Расчет. Проверим условие (218),
используя усилие обжатия при gsp < 1,0 Р2 = 520 кН. По формуле (219) вычисляем значение
Из примера 37 имеем e0p = 420 мм. Тогда Р2 (e0p
+ r) - 0,5Wred = 520 × 103 (420 + 328)
- 0,5 × 69 × 106 = = 335 × 106 Н · мм = 355
кН · м > Ml = 340
кН · м, т.е. от постоянных и
длительных нагрузок напряжения сжатия везде превышают 0,5 МПа. Для проверки
условия (217)
используем значение ss, вычисляемое в примере 37 при проверке
непродолжительного раскрытия трещин от действия всех нагрузок с учетом dnss = 257 МПа. Тогда ssp + ss = 640 + 257 = 897 МПа
< 0,8Rs,ser = 0,8 × 1335 = 1068 МПа, т.е. необратимые деформации
в арматуре возникнуть не могут. Таким образом, при постоянных и длительных
нагрузках трещины, образовавшиеся от всех нагрузок, надежно закрыты. РАСЧЕТ ЭЛЕМЕНТОВ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ ПО ДЕФОРМАЦИЯМ4.25 (4.22). Деформации (прогибы, углы
поворота) элементов железобетонных конструкций должны вычисляться по формулам
строительной механики, определяя входящие в них значения кривизны в
соответствии с указаниями пп. 4.27 - 4.35. Величины
кривизны и деформаций железобетонных элементов отсчитываются от их начального
состояния, т.е. от состояния до обжатия. 4.26 (4.23). Кривизна определяется: а) для участков
элемента, где в растянутой зоне не образуются трещины, нормальные к продольной
оси элемента, - как для сплошного тела; б) для участков
элемента, где в растянутой зоне имеются трещины, нормальные к продольной оси, -
как отношение разности средних деформаций крайнего волокна сжатой зоны бетона и
продольной растянутой арматуры к рабочей высоте сечения элемента. Элементы или
участки элементов рассматриваются без трещин в растянутой зоне, если трещины не
образуются под действием постоянных, длительных и кратковременных нагрузок или
если они закрыты при действии постоянных и длительных нагрузок, при этом
нагрузки вводятся в расчет с коэффициентом надежности по нагрузке gf = 1,0. Определение кривизны железобетонных элементов на участках без трещин в растянутой зоне4.27 (4.24). На участках, где не
образуются нормальные к продольной оси трещины, полная величина кривизны
изгибаемых, внецентренно сжатых и внецентренно растянутых элементов должна
определяться по формуле где здесь Msh, Ml - момент от соответствующей
внешней нагрузки относительно оси, нормальной к плоскости действия изгибающего
момента и проходящей через центр тяжести приведенного сечения; jb1 - коэффициент, учитывающий влияние кратковременной
ползучести бетона и принимаемый для бетонов: тяжелого, мелкозернистого и легкого при плотном мелком заполнителе......................................................................................................... 0,85 легкого при пористом мелком заполнителе................................................................. 0,70 jb2 - коэффициент, учитывающий
влияние длительной ползучести бетона на деформации элемента без трещин, принимаемый
по табл. 41;
здесь Îb, ΢b
- относительные деформации бетона, вызванные его усадкой и ползучестью от
усилия предварительного обжатия и определяемые соответственно на уровне центра
тяжести растянутой продольной арматуры и крайнего сжатого волокна бетона по
формулам:
Значение ssb принимается численно равным
сумме потерь предварительного напряжения арматуры от усадки и ползучести бетона
по поз. 6, 8 и 9 табл. 4 для арматуры растянутой зоны, а s¢sb - то же, для напрягаемой
арматуры, если бы она имелась на уровне крайнего сжатого волокна бетона (т.е. s¢sb определяется как при
наличии, так и отсутствии напрягаемой арматуры в сжатой зоне). Здесь ssb и s¢sb - в МПа. При определении ssb и s¢sb напряжения sbp находятся по формуле (10)
соответственно на уровне центра тяжести арматуры S и крайнего сжатого волокна бетона. Потери от усадки бетона при
определении s¢sb принимается равными нулю,
если в стадии изготовления в зоне, растянутой от действия усилия Р1, образуются трещины; в
этом случае ΢b = 0. Таблица 41 (34)
Примечания: 1. Влажность воздуха окружающей среды принимается согласно указаниям п. 1.5. 2. Группы мелкозернистого бетона приведены в п. 2.1. 3. При попеременном водонасыщении и высушивании бетона значения jb2 при продолжительном действии нагрузки следует умножать на коэффициент 1,2. 4. При влажности воздуха окружающей среды выше 75 % и при загружении бетона в водонасыщенном состоянии значения jb2 по поз. 2а настоящей таблицы следует умножать на коэффициент 0,8. Сумма В случае, когда
моменты М и Рe0p имеют одинаковые
направления вращения (например, на защемленных опорах балок), кривизна 4.28 (4.25). При определении кривизны участков элементов с начальными трещинами в сжатой
зоне (см. п. 4.5) значения 4.29 (4.26). На участках, где образуются нормальные трещины в растянутой зоне, но
при действии рассматриваемой нагрузки обеспечено их закрытие [т.е. выполняются условия (217) и (218)], значения кривизны Если кривизна,
определенная по пп. 4.30 - 4.32, оказывается
отрицательной, ее следует пересчитать по указаниям п. 4.27 и настоящего пункта [независимо от выполнения условий (217) и
(218)]. Определение кривизны железобетонных элементов на участках с трещинами в растянутой зоне4.30 (4.27). На участках, где в растянутой зоне образуются нормальные к продольной
оси элемента трещины, кривизна изгибаемых, внецентренно сжатых, а также
внецентренно растянутых при e0,tot ³ 0,8h0 [e0,tot - см. условие (205)] элементов прямоугольного, таврового и двутаврового (коробчатого)
сечений должна определяться по формуле где Ms - момент относительно оси,
нормальной к плоскости действия момента и проходящей через центр тяжести
площади сечения арматуры S,
от всех внешних сил и усилия предварительного обжатия Р; значение Ms вычисляется по формулам: для изгибаемых
элементов Ms = ± M ± Pesp; (227) для внецентренно
сжатых и внецентренно растянутых элементов Ms = ± Nes ± Pesp; (228) при этом знак
определяется направлением вращения моментов (черт. 50); за положительные
принимаются моменты, вызывающие растяжение в арматуре S; z - расстояние от центра
тяжести площади сечения арматуры S до
точки приложения равнодействующей усилий в сжатой зоне сечения над трещиной,
определяемое по указаниям п. 4.31; ys - коэффициент, учитывающий работу растянутого
бетона на участке с трещинами и определяемый по указаниям п. 4.32; yb - коэффициент, учитывающий неравномерность
распределения деформаций крайнего сжатого волокна бетона по длине участка с
трещинами и принимаемый равным 0,9, за исключением конструкций из легкого
бетона класса В7,5, для которых yb = 0,7; jf - коэффициент, определяемый
по формуле (235);
v - коэффициент, характеризующий
упругопластическое состояние бетона сжатой зоны и принимаемый по табл. 42; Ntot - равнодействующая
продольной силы N и усилия предварительного
обжатия Р: Ntot = P ± N; (229) в формуле (229)
растягивающее усилие N
принимается со знаком «минус», в формулу (226) усилие Ntot подставляется со своим знаком. При определении
кривизны элементов на участках с начальными трещинами в сжатой зоне (см. п. 4.5)
значение Р снижается путем умножения
на коэффициент q (см. п. 4.6). Таблица 42 (35)
Примечания: 1. Влажность воздуха окружающей среды принимается согласно указаниям п. 1.5. 2. Группы мелкозернистого бетона приведены в п. 2.1. 3. При попеременном водонасыщении и высушивании бетона значения v при продолжительном действии нагрузки следует умножать на коэффициент 1,2. 4. При влажности воздуха окружающей среды выше 75 % и при загружении бетона в водонасыщенном состоянии значения v по поз. 2а настоящей таблицы следует разделить на 0,8.
Черт. 50.
Определение заменяющего момента Ms и коэффициента jm для изгибаемого элемента Сечение 1 - 1: сечение
2 - 2: сечение
3 - 3: 1 - ядровая точка; 2 - центр тяжести площади приведенного сечения; 3 - центр тяжести площади арматуры S Для изгибаемых и
внецентренно сжатых элементов из тяжелого бетона при Mr < M0 кривизну допускается
определять с учетом работы растянутого бетона над трещинами по формуле и принимать не более
кривизны, определенной по формуле (226). Здесь
изгибаемых Ms = M0 + Pesp; внецентренно сжатых Ms = M0 + Nysr + Pesp, где ysr = y0 - а + r - расстояние от центра
тяжести растянутой арматуры до оси, проходящей через наиболее удаленную ядровую
точку (см. п. 4.2); Mr - момент, определяемый
согласно п. 4.2
от полной нагрузки, включающей постоянную, длительную и кратковременную
нагрузки; М0 - момент, при котором
растянутый бетон над трещинами выключается из работы, определяемый по формуле (201) п.
4.16б, в которой y уменьшается вдвое при учете
продолжительного действия постоянных и длительных нагрузок; Mcrc - см. п. 4.2; M, Mtot - моменты внешних сил
относительно оси, проходящей через центр тяжести сечения, соответственно от
рассматриваемой и полной нагрузок. 4.31 (4.28). Значение x вычисляется по формуле но принимается не более 1,0. Для второго
слагаемого правой части формулы (232) верхние знаки принимаются при сжимающем, а
нижние - при растягивающем усилии Ntot (см. п. 4.30). В формуле (232): b - коэффициент, принимаемый
равным для бетона: тяжелого и легкого................................................ 1,8 мелкозернистого.................................................... 1,6
es,tot - эксцентриситет силы Ntot относительно центра тяжести площади сечения
арматуры S; соответствует моменту Ms (см. п. 4.30) и
определяется по формуле При сжимающем усилии Ntot значение Значение z вычисляется по формуле Для внецентренно
сжатых элементов значение z
должно приниматься не более 0,97es,tot. Для элементов
прямоугольного сечения и таврового с полкой в растянутой зоне в формулах (234) и
(238)
вместо величины h¢f
подставляется величина 2а¢ или h¢f
= 0 соответственно при наличии или отсутствии арматуры S¢. Расчет сечений,
имеющих полку в сжатой зоне, при jf =
0; Расчетная ширина
полки b¢f
определяется согласно указаниям п. 3.16. Если 4.32 (4.29). Коэффициент ys определяется по формуле но не более 1,0; при этом
следует принимать es,tot /h0 ³ 1,2/jls. В формуле (239): jls - коэффициент, учитывающий влияние длительности
действия нагрузки и принимаемый равным: при непродолжительном действии нагрузки
для арматуры стержневой - 1,1, проволочной - 1,0; при продолжительном действии
нагрузки - 0,8; для конструкций из легкого бетона класса В7,5 указанные
значения jls снижаются на 0,3 и на 0,2
соответственно при непродолжительном и продолжительном действии нагрузок; es,tot - см. формулу (237); но не более
1,0; здесь Wpl - см. п. 4.3; Mr, Mrp - см. п. 4.2, при этом за положительные принимаются моменты,
вызывающие растяжение в арматуре S. 4.33. Кривизны внецентренно растянутых элементов при e0,tot < 0,8h [e0,tot - см. условие (205)] и при N > P на участках с нормальными трещинами определяются следующим образом: а) если
продольная сила Ntot приложена между центрами
тяжести площадей сечения арматуры S и S¢ (т.е. если e0,tot < ys0, где ys0 - расстояние от центра
тяжести площади сечения арматуры S до
центра тяжести приведенного сечения, кривизна определяется по формуле где zs = h0 - а¢ - расстояние между центрами
тяжести площадей арматуры S и S¢; es,tot = ys0 - e0,tot; ys, y¢s - коэффициенты, учитывающие работу растянутого
бетона соответственно для арматуры S и S¢ и определяемые по формулам: ys = 1 - jls Ncrc /Ntot; (242) y¢s = 1 - jls N¢crc /Ntot; (243) jls - коэффициент, принимаемый равным при действии
нагрузки: непродолжительном - 0,70, продолжительном - 0,35; Ncrc, N¢crc - усилия, приложенные в той же точке, что и сила Ntot, соответствующие
образованию трещин, соответственно в более растянутой зоне сечения и в менее
растянутой зоне; значения Ncrc и N¢crc определяются по формулам: и принимаются не более Ntot. Кроме того, при r¢ < e0,tot значение N¢crc принимается равным Ntot. В формуле (244): Wpl,
W¢pl - значения Wpl, определенные согласно п. 4.3
соответственно для более растянутой и менее растянутой сторон сечения; r, r¢ - расстояния от центра
тяжести приведенного сечения до ядровых точек, наиболее удаленных
соответственно от более растянутой и от менее растянутой сторон сечения;
значения r и r¢ определяется по формуле (170); б) если
продольная сила Ntot приложена вне расстояния
между центрами тяжести площадей арматуры S и S¢, кривизна определяется по
линейной интерполяции между кривизной Это
соответствует вычисление кривизны по формуле 4.34 (4.30). Полная величина кривизны где
Кривизны Если моменты от
внешних нагрузок и от усилия Р
относительно центра тяжести сечения арматуры S имеют одинаковое направление вращения (например, на защемленной опоре
неразрезной балки), кривизна 4.35. Полная величина кривизны где
Определение прогибов4.36 (4.31). Прогиб fm, обусловленный деформацией изгиба, определяется по формуле где
При определении
прогиба в середине пролета балочных элементов формула (248) может быть приведена к
виду где
n - четное число равных
участков, на которое разделен пролет элемента; число n
рекомендуется принимать не менее 6. В формулах (248) и
(249)
значения Черт. 51. Эпюра кривизн в
железобетонном элементе с переменным по длине сечением 4.37 (4.32). Для изгибаемых элементов при 4.38 (4.33). Прогиб fq, обусловленный деформацией сдвига, определяется по формуле
где gх - деформация сдвига,
определяемая по формуле
здесь Qx - поперечная сила в сечении
х от действия внешней нагрузки; G - модуль сдвига бетона (см.
п. 2.12); jb2 - коэффициент, учитывающий влияние длительной
ползучести бетона и принимаемый по табл. 41; jcrc - коэффициент, учитывающий
влияние трещин на деформации сдвига и принимаемый равным: на участках по длине
элемента, где отсутствуют нормальные и наклонные к продольной оси элемента
трещины, - 1,0; на участках, где имеются только наклонные к продольной оси
элемента трещины, - 4,8; на участках, где имеются только нормальные или
нормальные и наклонные к продольной оси элемента трещины, - по формуле
где Мх,
4.39. Контрольный прогиб элемента, используемый при оценке
жесткости конструкций согласно ГОСТ
8829-85, определяется по формуле fк = f1 ± f2, (253) где f1 - полный прогиб элемента от
действия всей внешней нагрузки (контрольной и от собственного веса) и усилия
предварительного обжатия, вычисляемый согласно указаниям пп. 4.36 - 4.38; f2 - выгиб (принимается со
знаком «плюс», черт. 52, а)
или прогиб (принимается со знаком «минус», черт. 52, б) от собственного веса и усилия предварительного обжатия; при
этом, если в верхней зоне элемента образуются начальные трещины, значение f2 определяется как для
элемента с трещинами в верхней зоне (т.е. элемент рассматривается в
перевернутом положении). Черт. 52. Определение контрольного прогиба fк, замеряемого
при испытании а - при наличии перед началом испытания выгиба f2; б - при наличии перед началом испытания прогиба f1 Значения f1 и f2 определяются согласно
указаниям пп. 4.36
- 4.38,
4.43,
4.44,
принимая непродолжительное действие нагрузок, при этом кривизна Если при действии
всей внешней нагрузки трещины в растянутой зоне не образуются и, кроме того,
отсутствуют начальные трещины в сжатой зоне, контрольный прогиб fк можно определить по формуле
где Mcon - момент от контрольной
нагрузки (внешней нагрузки без учета собственного веса); rm - см. табл. 46. Определение продольных деформаций4.40. Относительные деформации Î0 (удлинения или укорочения)
в направлении продольной оси элементов определяются следующим образом: 1. Относительные
деформации внецентренно сжатых и внецентренно растянутых элементов с
однозначной эпюрой напряжений определяют: а) для
внецентренно сжатых элементов или их отдельных участков, не имеющих трещин в
растянутой зоне, - по формуле где v - см. п. 4.30; б) для участков
внецентренно сжатых элементов, в которых от действия полной нагрузки образуются
трещины в растянутой зоне, - по формуле (255) с последующим увеличением на 20 %. в) для
внецентренно растянутых элементов или их участков при отсутствии трещин - по
формуле где jb1, jb2 - см. п. 4.27; в формулах (255)
и (256)
знак «плюс» соответствует деформациям укорочения, знак «минус» - деформациям
удлинения; г) то же, при
наличии трещин (т.е. для элементов, указанных в п. 4.33а) - по формуле где Îsm, ΢sm - соответственно средние величины удлинения арматуры S и S¢, определяемые по формулам: здесь Ntot, es,tot, ys, y¢s, zs - см. п. 4.33а. 2. Относительные
деформации изгибаемых, внецентренно сжатых и внецентренно растянутых элементов
с двухзначной эпюрой напряжений в сечении определяют: а) для элементов
или их отдельных участков, не имеющих трещин в растянутой зоне, - по формуле
где jb1, jb2 - см. п. 4.27; v - см. п. 4.30; правило знаков
то же, что и для формул (255)
и (256); б) для участков
элементов, указанных в п. 4.30, имеющих трещины в растянутой зоне, - по формуле где Îsm, Îbm - соответственно средние величины относительного
удлинения арматуры и относительного укорочения крайнего сжатого волокна бетона
на участке между трещинами, определяемые по формулам:
здесь Ms, ys, yb, z, jf, x, Ntot - см. пп. 4.30 - 4.32; в) для участков
внецентренно растянутых элементов, указанных в п. 4.33б, значение Î0 определяется по линейной
интерполяции между значением Î0, определенным по формуле (257)
при es,tot = 0 (т.е. при e0,tot = ys0), и значением Î0, определенным по формуле (260)
при Ms = Ntot (0,8h0 - ys0), (т.е. при e0,tot = 0,8h0), где ys0 - см. п. 4.33. ys - расстояние от рассматриваемого волокна до центра тяжести арматуры S; y -
то же, до центра тяжести приведенного сечения. Деформации Î0, найденные по формулам
настоящего пункта, со знаком «плюс» отвечают укорочению, а со знаком «минус» -
удлинению. При
одновременном действии кратковременной и длительной нагрузок порядок вычисления
Î0 аналогичен определению
полной кривизны согласно п. 4.34. 4.41. Укорочение (удлинение) элементов на уровне
рассматриваемого волокна определяется по формуле где Î0i - относительные продольные
деформации в сечении, расположенном посередине участка длиной li; n - число участков, на
которые разбивается длина элемента. Прогибы ферм
определяются по формуле
где Dli - укорочение (удлинение) i-го стержня фермы,
определяемое по формуле (263) на уровне центра тяжести сечения. Приближенные методы расчета по деформациям4.42. Прогибы железобетонных изгибаемых элементов постоянного сечения,
эксплуатируемых при влажности воздуха окружающей среды выше 40 %, заведомо
меньше предельно допустимых, если выполняется условие l/h0 £ llim, (265) где llim - граничное отношение
пролета элемента к рабочей высоте сечения, определяемое по табл. 43. При l0/h < 10 прогибы заведомо меньше предельно допустимых, если выполняется
условие (266),
учитывающее влияние поперечных сил на деформации элемента, Таблица 43
Примечание. Значения llim, приведенные над чертой, применяются при армировании стержневой арматурой классов А-IIIв, А-IV и А-V; под чертой - арматурой класса А-VI и проволочной.
Табличные
значения llim отвечают продолжительному
действию равномерно распределенной нагрузки на свободно опертую балку при
предельно допустимом прогибе, равном l/200.
Причем напрягаемая арматура принята с максимально допустимыми значениями ssp, соответствующими указаниям
пп. 1.15 и 1.22, при максимально возможных
потерях напряжений. Если предельно
допустимые прогибы f
(см. п. 1.14) меньше l/200, табличные значения llim должны быть уменьшены в (l/200
: f/l) раз (например, при f/l = 1/300 - в 1,5 раза). Примечание. Если нагрузка отличается от
равномерно распределенной, значения коэффициента llim могут быть увеличены путем умножения его табличных
значений на отношение Определение кривизны4.43. Для изгибаемых и внецентренно сжатых элементов прямоугольного,
таврового и двутаврового (коробчатого) сечений, эксплуатируемых при влажности
воздуха окружающей среды выше 40 %, кривизну на участках с трещинами (Mr > Mcrc) в растянутой зоне
допускается определять по формуле1 1 Определение кривизны по формуле (267) для указанных элементов соответствует расчету по формулам (226) - (240). где Ms, Ntot - см. п. 4.30; r - см. п. 4.2; ys0 - расстояние от центра
тяжести приведенного сечения до центра тяжести сечения арматуры S; Таблица 44
Таблица 45
Полную кривизну для
указанных выше элементов допускается определять по формуле1 1 Определение полной кривизны по формуле (268) соответствует расчету по формуле (246). Здесь Ms,sh, Ms,l - моменты Ms (см. п. 4.30)
соответственно от кратковременных нагрузок (см. п. 1.8) и от продолжительного
действия постоянных и длительных нагрузок; j1,sh - коэффициент j1, отвечающий
непродолжительному действию нагрузки; j1l, j2l, j3l - коэффициенты j1, j2 и j3, отвечающие
продолжительному действию нагрузки; При определении
кривизны элемента на участках с начальными трещинами в сжатой зоне усилие Ntot = P + N определяется с учетом
снижения значения Р путем умножения
на коэффициент q (см. п. 4.6). Определение прогибов4.44. Для изгибаемых элементов при l/h ³ 10 прогиб определяется следующим образом: а) для элементов
постоянного сечения, работающих как свободно опертые или консольные балки,
прогиб допускается определять, вычисляя кривизну где rm - см. табл. 46; кривизна Таблица 46
Примечание. При загружении элемента одновременно по нескольким из представленных в табл. 46 схемам коэффициент rm равен:
где rm1 и M1, rm2 и М2 и т.д. - соответственно коэффициент rm и наибольший момент для каждой схемы загружения. Черт. 53. Эпюра изгибающих моментов и соответствующая ей расчетная
эпюра кривизны при упрощенном определении прогиба а - расчетная схема; б - эпюра изгибающих моментов; в - эпюра кривизн; lcrcl - длина участка без трещин при действии всех нагрузок; M1 - момент от рассматриваемой нагрузки на границе участка без трещин При схемах
загружения элемента, не представленных в табл. 46, прогиб определяется по
формулам строительной механики при постоянной жесткости, равной отношению б) если прогиб,
определенный по подпункту «а», превышает допустимый, то его значение
рекомендуется уточнить за счет учета переменной по длине жесткости; при
равномерно распределенной нагрузке (черт. 53) это соответствует формуле где r1 - коэффициент,
определяемый: для свободно
опертой балки - по табл. 47 в зависимости от отношения Mcrc/Mtot (Mtot - наибольший изгибающий момент от постоянных, длительных и
кратковременных нагрузок); для консоли - по
формуле r1 = 0,25 Mcrc/Mtot; r2 - коэффициент, принимаемый
равным: для свободно опертой балки - 1/48; для консоли - 1/4;
при других
схемах загружения прогиб определяется по формуле (272); Таблица 47
в) для элементов
с защемленными опорами прогиб может определяться по формуле где rm - коэффициент, определяемый по табл. 46 как
для свободно опертой балки; г) для элементов
переменного сечения, а также в тех случаях, когда требуется более точное, чем
по формулам (269)
и (271),
определение прогибов, а сами элементы и нагрузка симметричны относительно
середины пролета, прогиб определяется по формуле где Входящие в
формулы (271)
и (272)
значения кривизны определяются по формулам (246), (247), (268)
при наличии трещин в растянутой зоне и по формуле (221) - при их отсутствии. При
несимметричном расположении нагрузки прогиб определяется по формуле (249). 4.45. Для коротких элементов (l/h < 10) постоянного
сечения, работающих как свободно опертые балки, прогиб вычисляется согласно п. 4.44 и
умножается на коэффициент rq, учитывающий влияние деформаций сдвига. Коэффициент
rq определяется по формуле
где jq = 0,5 - при отсутствии как
нормальных, так и наклонных трещин, т.е. при выполнении условий (163) и
(183); jq = 1,5 - при наличии нормальных или наклонных
трещин; rm - см. табл. 46. Примеры расчетаПример 40. Дано:
плита перекрытия - по черт. 44; расчетный пролет плиты l = 5,7 м; нагрузка,
равномерно распределенная; в середине пролета момент от полной нагрузки Mtot = 66 кН · м, от постоянной
и длительной нагрузок Ml = 63,8 кН · м; усилие предварительного обжатия с учетом всех потерь и
влияния верхних трещин Р2
= 109 кН; потери напряжения от усадки и ползучести бетона на уровне
предварительно напряженной арматуры (поз. 6, 8, 9 табл. 4) ssb = 168 МПа; влажность
воздуха в пределах 40 - 75 %; прогиб ограничивается эстетическими требованиями;
остальные данные - по примеру 31. Требуется рассчитать плиту по деформациям. Расчет. Определяем необходимость
вычисления прогиба плиты согласно п. 4.42. Для этого находим
величины l/h0, jf, ma:
(v = 0,15, так как влажность воздуха в пределах 40 - 75 % и расчет
ведется на продолжительное действие нагрузки). При ma = 0,14, jf = 0,71 и jft = 0 из табл. 43
находим llim = 12,5 < l/h0 = 19, т.е. расчет по деформациям необходим.
Кривизну элемента Ms = M
+ P2 esp = 63,8 × 106
+ 109 × 103 × 5 =
64,3 кН · м (esp = y0
- e0p - a = 220 - 165 -
50 = 5 мм); ys = y0 - а = 220 - 50 = 170 мм;
= 1,03 × 10-5 1/мм. Определяем по
формуле (224)
кривизну
΢b = 0, так как в верхней зоне
элемента имеются трещины обжатия.
[коэффициент 1,25 учитывает
увеличение Полная кривизна
в середине пролета равна:
Прогиб плиты
определяем по формуле (269):
([f] = 25 мм принят согласно
табл. 3), т.е. прогиб плиты меньше предельно
допустимого. Пример 41. Дано:
многопустотная плита перекрытия с эквивалентным сечением - по черт. 54
(определение эквивалентного сечения см. пример 30); расчетный пролет l = 8,86 м; бетон тяжелый
класса В30 (Eb = 29 × 103 МПа, Rbt,ser = 1,8 МПа, Rb,ser = 22 МПа); нагрузки:
постоянная и длительная - ql = 12,74 кН/м, полная - q =
14,37 кН/м; момент инерции приведенного сечения Ired = 1147,2 × 106 мм4; момент
сопротивления относительно нижней грани Wpl = 1690 × 104 мм3; потери
предварительных напряжений от усадки и ползучести на уровне напрягаемой
арматуры ssb = 80,1 МПа, то же, на
уровне верхней грани - s¢sb = 43,5 МПа; усилие обжатия
с учетом всех потерь Р = 807 кН; его
эксцентриситет относительно центра тяжести сечения е0р = 78 мм;
момент обжатия Mrp = 108 кН · м; момент
образования трещин Mcrc = 138,4 кН · м; прогиб ограничивается эстетическими требованиями. Требуется рассчитать плиту по деформациям. Расчет. Поскольку прогиб
ограничивается эстетическими требованиями, определим прогиб на действие
постоянных и длительных нагрузок. Момент в середине пролета от этих нагрузок
равен:
Черт. 54. К примеру расчета 41 Момент от всех нагрузок
равен:
Поскольку Mtot = 141 кН · м > Mcrc = 138,4 кН · м, кривизну
плиты в середине пролета определяем с учетом трещин по формулам пп. 4.30 - 4.32 при
M = Ml = 125 кН · м h0 = h - a = 220 - 27 = 193 мм (см.
черт. 54). Так как Mtot незначительно превышает Mcrc, кривизну Определим
значение М0 по формуле (201).
Для этого вычислим
Принимаем y = 0,6. Поскольку действие
нагрузок продолжительное, уменьшаем y вдвое, т.е. y = 0,3. Тогда М0 = Mcrc + ybh2Rbt,ser = 138,4 × 106 + 0,3 × 470 × 2202 × 1,8 = 150,7 × 106 Н · мм.
Определяем кривизну
Определяем кривизну Ntot = P
= 807 кН; значения x и z определим согласно п. 4.31:
b = 1,8;
Определим
значение ys согласно п. 4.32.
Для этого по формуле (240) вычисляем коэффициент jm, принимая Mr = М0 = 150,7 × 106 Н · мм:
Поскольку es,tot/h0 = 0,968 < 1,2/jls =
Принимаем v = 0,15 и yb = 0,9. Тогда
Приняв Mr = Mtot = 141 кН · м, определяем
кривизну в середине пролета по формуле (230):
= 0,69 × 10-5 1/мм. Определяем кривизну
Полная кривизна в середине
пролета равна:
Прогиб определим по формуле
(269),
принимая из табл. 46
Поскольку
вычисленный прогиб больше предельно допустимого, определяем его более точно по
формуле (270).
Для этого находим кривизны
Поскольку
= 0,223 × 10-5 × 2 = 0,446 × 10-5 1/мм, принимаем Тогда
= Из табл. 47 при Тогда
= 31,4 мм < [f] = 35,4 мм, т.е. прогиб плиты меньше
допустимого. Пример 42. Дано:
элемент нижнего пояса фермы с размерами поперечного сечения: h = 280 мм, b = 250 мм, а =
а¢ = 40 мм; продольная
растягивающая сила от постоянных и длительных нагрузок Nl = 820 кН; момент от этих
нагрузок Ml = 30 кН · м; усилие
предварительного обжатия с учетом всех потерь Р2 = 650 кН; остальные данные - по примеру 29. Требуется определить кривизну элемента и продольную осевую
относительную деформацию. Расчет. h0 = 280 - 40 = 240 мм.
Поскольку Nl > P2, определим эксцентриситет
равнодействующей усилий Ntot = Nl - P2 = 820 - 650 = 170 кН по
формуле (205),
принимая e0p = 0 и Nle0 = 30 кН · м:
= 0,8 × 240 = 192 мм. Кроме того, Из примера 29 имеем:
Rbt,ser = 1,95 МПа; Wpl = 7,61 × 106 мм2; r = 76 мм. Тогда
Определяем коэффициент ys, принимая jls = 0,35:
zs = h0 - а¢ = 240 - 40 = 200 мм. Тогда
Кривизну
v = 0,15 и Ntot = P2 - Nl = - 170 кН. Определяем
значения x и z согласно п. 4.31:
Так как x = 0,038 <
При jf = 0 формула (238)
принимает вид z = h0 (1 - 0,5x) = 240 (1 - 0,5 × 0,202) = 216 мм. Определяем
значение ys согласно п. 4.32,
принимая jls = 0,8. Из примера 30 имеем Mrp = 49,4 кН · м. Mr = Nl
(e0 + r) =
Ml + Nl r = 30 × 106
+ 820 × 103 × 76
= 92,3 × 106 Н · мм;
Принимаем
Определяем кривизну
Окончательная
кривизна сечения равна:
Продольное
относительное удлинение на уровне центра тяжести сечения также определим по
интерполяции согласно п. 4.40. Значение Î0I
определяем по формуле (257), принимая ys = ys0 = 100 мм и es,tot = 0, при этом формулы (258)
приобретают вид:
Тогда
Значение Î0II
определяем по формуле (260) при Ms = 15,64 × 106 Н · мм, ys = ys0 = 100 мм и Ntot = - 170 кН. Для этого
вычислим:
= 0,797 × 10-3;
Полученные
деформации Îsm и Îbm можно проверить, определив
по ним кривизну
т.е. деформации Îsm и Îbm вычислены правильно. Тогда
Окончательное
значение Î0 определяем по формуле,
аналогичной формуле (245):
Знак «минус»
означает, что в данном сечении имеет место деформация удлинения, отсчитываемая
от состояния до обжатия элемента. 5. КОНСТРУКТИВНЫЕ ТРЕБОВАНИЯОбщие
требования
5.1 (5.1). При проектировании
предварительно напряженных железобетонных конструкций для обеспечения условий их
изготовления, требуемой долговечности и совместной работы арматуры и бетона
надлежит выполнять конструктивные требования, изложенные в настоящем разделе. 5.2 (1.30). Для сборных элементов рекомендуется производить
натяжение арматуры на упоры до бетонирования изделия. Натяжение арматуры на
затвердевший бетон производится в монолитных конструкциях, в крупных балках,
трубах и т.п., а также в целях создания неразрезных статически неопределимых
конструкций. При этом, как правило, в целях обеспечения совместной работы
арматуры и бетона, а также защиты арматуры от коррозии каналы, пазы и выемки
для пропуска арматуры должны заполняться (инъецироваться) цементным раствором
или мелкозернистым бетоном. Примечание. Для предварительно напряженных конструкций, в которых предусматривается регулирование напряжений обжатия бетона в процессе их эксплуатации (например, в реакторах, резервуарах, телевизионных башнях), напрягаемая арматура применяется без сцепления с бетоном; при этом необходимо предусматривать эффективные мероприятия по защите арматуры от коррозии. Расчет таких конструкций по прочности следует производить по специальным указаниям. 5.3 (5.54). Схемы и способы возведения статически неопределимых
предварительно напряженных конструкций рекомендуется выбирать так, чтобы при
создании предварительного напряжения исключалась возможность возникновения в
конструкции дополнительных усилий, ухудшающих их работу. Допускается устройство
временных швов или шарниров, замоноличиваемых после натяжения арматуры. 5.4. Способ натяжения арматуры принимается в соответствии
с указаниями «Руководства по технологии изготовления предварительно напряженных
железобетонных конструкций» (М., Стройиздат, 1975). 5.5. Следует использовать по возможности арматуру,
закладные детали и строповочные петли, выпускаемые в виде товарной продукции в
соответствии с государственными стандартами и нормалями. Ненапрягаеую арматуру
следует проектировать в виде укрупненных блоков и пространственных каркасов для
сокращения времени укладки в форму (опалубку). 5.6. С целью снижения расхода цемента, ускорения оборота
форм и интенсивного использования производственных площадей передаточную
(распалубочную) прочность бетона рекомендуется назначать минимально допустимой
(см. п. 2.3), если это не приводит к заметному снижению допустимых нагрузок,
определяемых требованиями второй группы предельных состояний. 5.7. Необходимо стремиться к унификации арматуры и
закладных деталей в отдельных конструкциях и их сериях, к небольшому количеству
разных марок и диаметров стали, типов арматурных элементов - сеток и каркасов,
шагов продольных и поперечных стержней. Габариты
и очертания элементов конструкций
5.8 (5.2,
5.3). Минимальные
размеры сечения железобетонных элементов, определяемые из расчета по
действующим усилиям и соответствующим группам предельных состояний, должны
назначаться с учетом экономических требований, необходимости унификации
опалубучных форм и армирования, а также условий принятой технологии
изготовления конструкций. Кроме того,
размеры сечения элементов железобетонных конструкций должны приниматься такими,
чтобы соблюдались требования в части расположения арматуры в сечении (толщины
защитных слоев бетона, расстояния между стержнями и т.п.) и анкеровки арматуры. Размеры сечений
внецентренно сжатых элементов должны приниматься такими, чтобы их гибкость l0/i в любом направлении, как правило, не превышала для железобетонных
элементов из тяжелого, мелкозернистого и легкого бетонов - 200 (для
прямоугольных сечений l0/h £ 60), а для колонн, являющихся элементами
зданий, - 120 (l0/h £ 35). При назначении
размеров следует учитывать также условия перевозки: транспортные средства и
допустимые габариты. 5.9. При проектировании бетонных и железобетонных
конструкций их очертание следует принимать с учетом устройства и способа использования
форм (опалубки). При применении
форм с откидными бортами очертание изделия не должно препятствовать повороту
борта (черт. 55,
а) при распалубке. Черт. 55. Технологические уклоны а - в форме с откидными бортами; б - позволяющие изделию самораспалубливаться при передаче предварительных напряжений на бетон; в - в неразъемной форме; г - то же, с применением выпрессовщика или при самораспалубливании; д, е - при немедленной распалубке; ж - в форме с глухим бортом; з - то же, с выпрессовщиком; 1 - изделие; 2 - форма; 3 - откидной борт; 4 - выпрессовщик; 5 - вкладыш; 6 - формующая рамка При передаче
предварительных напряжений на бетон последний должен иметь возможность свободно
деформироваться. Это обеспечивается освобождением его к этому моменту от
сдерживающих элементов формы, применением резиновых компенсаторов или наличием
плавных скосов, позволяющих изделию самораспалубливаться при обжатии. Пример
скоса приведен на черт. 55, б. При применении
неразъемных форм для возможности извлечения изделия из формы должны
предусматриваться уклоны не менее 1 : 10 (черт. 55, в). При неразъемных формах, если при обжатии в результате выгиба
создается сила, выталкивающая затвердевший бетон из формы, или если
используется выпрессовывание, уклоны должны быть не менее 1 : 15 (черт. 55, г). При немедленной
распалубке с обеспечением фиксированного (во избежание нарушения бетона)
вертикального перемещения формующего элемента оснастки (черт. 55, д, е)
уклон должен быть не менее 1 : 50. При
использовании форм с одним неподвижным и одним откидным бортом для возможности
вертикального подъема конструкции при распалубке следует переход от большей
ширины изделий к меньшей, например от нижней полки к стенке (черт. 55, ж), принимать плавным под углом не менее
45°. Это требование можно не предъявлять, если
форма снабжена выпрессовывающим устройством (черт. 55, з). Применение
выпрессовывания и немедленной распалубки должно согласовываться с изготовителем
изделия. 5.10. Сборные железобетонные изделия рекомендуется
проектировать с учетом изготовления их по возможности в максимально неразборных
формах. Если невозможно
изготовление изделия в полностью неразборной форме, рекомендуется
предусматривать наибольшую поверхность формы неразборной. 5.11. Очертания сборных железобетонных изделий следует
принимать наиболее простыми. Ребра в стенках балок целесообразно
предусматривать лишь при больших сосредоточенных нагрузках или при
необходимости обеспечения устойчивости стенки. 5.12. Во избежание повреждений от местных концентраций
напряжений при резком изменении направлений граней изделия, например во
внутренних углах, рекомендуется предусматривать смягчение очертания в виде
уклонов, фасок или закруглений по возможности небольшой величины (до 50 мм),
чтобы не требовалось местное армирование (черт. 56, а - г). Во внешних
острых углах во избежание откалывания бетона следует устраивать скосы или
закругления (черт. 56, д). Черт. 56. Закругления и фаски а - ребристая плита, закругление; б - тавровая балка, фаска между полкой и стенкой; в - узел фермы, сочетание фаски и закруглений; г - отверстие в железобетонном элементе для пропуска коммуникаций, закругления; д - смягчение острого угла в ригеле Защитный
слой бетона
5.13 (5.4). Защитный слой бетона для
рабочей арматуры должен обеспечивать совместную работу арматуры с бетоном на
всех стадиях работы конструкции, а также защиту арматуры от внешних
атмосферных, температурных и подобных воздействий. 5.14 (5.5). Для продольной рабочей
арматуры (ненапрягаемой и напрягаемой, натягиваемой на упоры) толщина защитного
слоя должна быть, как правило, не менее диаметра стержня или каната и не менее,
мм: в плитах и стенках толщиной, мм: до 100 включ...................................................... 10 св. 100.................................................................. 15 в балках и ребрах высотой, мм: менее 250............................................................ 15 250 и более......................................................... 20 в колоннах.................................................................. 20 Для сборных элементов из
тяжелого бетона класса В20 и выше толщину защитного слоя продольной арматуры
допускается принимать на 5 мм меньше диаметра стержня, но не менее величин,
указанных выше. Для
железобетонных плит из тяжелого бетона класса В20 и выше, изготовляемых на
заводах в металлических формах и защищаемых сверху в сооружении бетонной
подготовкой или стяжкой, толщину защитного слоя для верхней арматуры
допускается принимать равной 5 мм. В однослойных
конструкциях из легкого бетона класса В7,5 толщина защитного слоя должна
составлять не менее 20 мм, а для наружных стеновых панелей (без фактурного
слоя) - не менее 25 мм. 5.15 (5.6). Толщина защитного слоя
бетона для поперечной, распределительной и конструктивной арматуры должна
приниматься не менее диаметра указанной арматуры и не менее, мм: при высоте сечения элемента менее 250 мм........................................................................ 10 то же, равной 250 мм и более................................ 15 В элементах из легкого
бетона класса В7,5 независимо от высоты сечения толщина защитного слоя бетона
для поперечной арматуры принимается не менее 15 мм. 5.16 (5.7). Толщина защитного слоя
бетона у концов предварительно напряженных элементов на длине зоны передачи напряжений
(см. п. 2.26) должна составлять не менее: для стержневой
арматуры классов А-IV и А-IIIв, а также для арматурных
канатов - 2d; для стержневой
арматуры классов А-V, A-VI - 3d. Кроме того,
толщина защитного слоя бетона на указанном участке длины элемента должна быть
не менее 40 мм - для стержневой арматуры всех классов и не менее 20 мм - для
арматурных канатов. Допускается
защитный слой бетона для сечения у опоры для напрягаемой арматуры с анкерами и
без них принимать таким же, как и для сечений в пролете, в следующих случаях: а) для
предварительно напряженных элементов с сосредоточенной передачей опорных усилий
при наличии стальной опорной детали и косвенной арматуры (сварных поперечных
сеток или охватывающих продольную арматуру хомутов) - согласно указаниям п. 5.46; б) в плитах,
панелях, настилах и опорах ЛЭП при условии постановки у концов дополнительной
поперечной арматуры (корытообразных сварных сеток или замкнутых хомутов),
предусмотренной п. 5.46; при этом диаметр поперечной арматуры
рекомендуется принимать не менее 0,25 диаметра продольной напрягаемой арматуры. 5.17 (5.8). В элементах с напрягаемой
продольной арматурой, натягиваемой на бетон и располагаемой в каналах,
расстояние от поверхности элемента до поверхности канала должно приниматься не
менее 40 мм и не менее ширины канала; указанное расстояние до боковых граней
элемента должно быть, кроме того, не менее половины высоты канала. При расположении
напрягаемой арматуры в пазах или снаружи сечения элемента толщина защитного
слоя бетона, образуемого последующим торкретированием или иным способом, должна
приниматься не менее 20 мм. 5.18 (5.10). В полых элементах кольцевого или коробчатого сечения
расстояние от стержней продольной арматуры до внутренней поверхности бетона
должно удовлетворять требованиям пп. 5.14 и 5.15. 5.19. Концы напрягаемой арматуры, а также анкеры должны
быть защищены антикоррозионным покрытием или слоем раствора не менее 5 мм или
слоем бетона не менее 10 мм. Минимальные
расстояния между стержнями арматуры
5.20 (5.11). Расстояния в свету между стержнями арматуры (или
оболочками каналов) по высоте и ширине сечения должны обеспечивать совместную
работу арматуры с бетоном и назначаться с учетом удобства укладки и уплотнения
бетонной смеси, а также с учетом степени местного обжатия бетона и габаритов
натяжного оборудования (домкратов, зажимов и т.п.) и концевых технологических
анкеров на стержнях (см. п. 5.26). 5.21 (5.12). Расстояние в свету между отдельными стержнями продольной ненапрягаемой арматуры либо напрягаемой арматуры, натягиваемой на упоры,
а также между продольными стержнями соседних плоских сварных каркасов должны
приниматься не менее наибольшего диаметра стержней, а также: а) если стержни
при бетонировании занимают горизонтальное или наклонное положение - не менее:
для нижней арматуры - 25 мм и для верхней арматуры - 30 мм; при расположении
нижней арматуры более чем в два ряда по высоте расстояние между стержнями в
горизонтальном направлении (кроме стержней двух нижних рядов) должно быть не
менее 50 мм; б) если стержни
при бетонировании занимают вертикальное положение - не менее 50 мм; при
систематическом контроле фракционирования заполнителей бетона это расстояние
может быть уменьшено до 35 мм, но при этом должно быть не менее
полуторакратного наибольшего размера крупного заполнителя. В элементах или
узлах с большим насыщением арматурой или закладными деталями, изготовляемых без
применения виброплощадок или вибраторов, укрепленных на опалубке, должно быть
обеспечено в отдельных местах свободное расстояние в свету не менее 60 мм для
прохождения между арматурными стержнями наконечников глубинных вибраторов,
уплотняющих бетонную смесь. Расстояние между такими местами должно быть не
более 500 мм. 5.22 (5.12). При стесненных условиях допускается располагать стержни арматуры
попарно (без зазора между ними). Такая пара стержней при назначении расстояний
между стержнями по п. 5.21 и при определении длины
передачи напряжений или длины анкеровки (по пп. 2.26
и 5.32) должна рассматриваться как
условный стержень диаметром 5.23 (5.12). Указанные в пп. 5.21 и 5.22 расстояния в свету между
стержнями периодического профиля определяются по номинальному диаметру без
учета выступов и ребер. При компоновке расположения арматуры в сечении со
стесненными условиями с учетом примыкающих других арматурных элементов и
закладных деталей следует принимать во внимание диаметры стержней с учетом
выступов и ребер, а также допускаемые отклонения от номинальных размеров
стержней арматуры, сварных сеток и каркасов, закладных деталей, формы и
расположения арматуры и закладных деталей в сечении. Черт. 57. Примеры расположения одного из рядов стержней нижней арматуры
(располагаемой в один или два ряда по высоте) в случае изготовления изделия на
виброплощадке а, б - варианты расположения стержней диаметром 32 мм; в, г - то же, диаметром 16 мм; а, в - одиночное расположение стержней; б, г - спаренное расположение стержней 5.24 (5.13,
5.59). В
элементах с напрягаемой арматурой, натягиваемой на бетон (за исключением
непрерывно армированных конструкций), расстояние в свету между каналами для
арматуры должно быть, как правило, не менее диаметра канала и не менее 50 мм. При проволочной
арматуре, расположенной в виде пучка, должны предусматриваться зазоры между
отдельными проволоками или группами проволок (путем установки спиралей внутри
пучка, коротышей в анкерах и т.п.) с размерами, достаточными для прохождения
между проволоками пучка цементного раствора или мелкозернистого бетона при
заполнении каналов. Черт. 58. Сечение канала с арматурным пучком из 24 проволок диаметром 5
мм при инъецировании канала раствором через отверстие в анкере 1 - арматурные коротыши в анкерах При
инъецировании канала через отверстие в анкере проволоки или группы проволок
пучка должны располагаться по окружности (черт. 58), при этом внутренний диаметр
канала должен превышать диаметр пучка не менее чем на 15 мм. АНКЕРОВКА АРМАТУРЫАнкеровка напрягаемой арматуры5.25 (5.61). Установка анкеров у концов арматуры обязательна для
арматуры, натягиваемой на бетон, а также для арматуры, натягиваемой на упоры,
при недостаточном ее сцеплении с бетоном (гладкой проволоки, многопрядных
канатов) и если не обеспечено отсутствие трещин на длине зоны передачи
напряжений (см. пп. 1.11 и 2.26); при этом анкерные устройства должны
обеспечивать надежную заделку арматуры в бетоне на всех стадиях ее работы.
Кроме того, рекомендуется установка анкеров, если в соответствии с расчетом
наклонного сечения на действие изгибающего момента (см. пп. 3.31 - 3.33)
необходимо существенно увеличить поперечное армирование. 5.26. Тип анкера выбирается исходя из производственных возможностей и вида
арматуры. Для стержневой
арматуры рекомендуется применять следующие типы временных технологических или
постоянных анкеров в виде: высаженных
головок (черт. 59,
а) - для арматуры классов A-V и A-IV
(марки 20ХГ2Ц); обжатых шайб
(черт. 59,
б и табл. 48) - для арматуры классов A-IV, A-V и A-VI; приваренных
коротышей (черт. 59, в) -
для арматуры классов A-V, Ат-IVC и A-IV
(марки 20ХГ2Ц). Черт. 59. Временные технологические анкеры на напрягаемой стержневой
арматуре а - высаженная головка; б - обжатая шайба (размеры см. табл. 48); в - приваренные коротыши Таблица 48
Для арматурных канатов
рекомендуется использовать временные анкеры в виде инвентарных цанговых зажимов
на один канат каждый (табл. 49). Габариты анкерных устройств должны
учитываться при назначении расстояний между осями натягиваемых стержней. Таблица 49
5.27. Для
арматурной проволоки класса Вр-II, натягиваемой на упоры в
виде пакетов, используются унифицированные напрягаемые арматурные элементы
(УНАЭ), основные параметры которых приведены на черт. 60. Эти элементы обозначаются
следующим образом: где n - число проволок в
элементе; А - площадь поперечного
сечения, мм2; N - суммарное разрывное
усилие, Н, определенное по нормативному сопротивлению. Элементы УНАЭ
могут группироваться по несколько штук и натягиваться с помощью общего захватного
устройства. Черт. 60. Основные параметры унифицированных напрягаемых арматурных
элементов а - на 3 проволоки; б - на n проволок (где n = 4, 6, 8, ..., 14) 5.28. Для стержневой арматуры, натягиваемой на бетон,
применяются анкеры в виде гаек на нарезных наконечниках, привариваемых к концам
стержней. Для арматурных пучков, натягиваемых на бетон, могут применяться
анкеры в виде металлических колодок и конусных пробок, анкеры с высаженными на
проволоках головками и др. 5.29. В конструкциях с арматурой криволинейного очертания
анкерные устройства целесообразно размещать на торцах элемента без увеличения
толщины нижнего защитного слоя бетона. В этом случае пучки или стержни арматуры
должны располагаться по высоте поперечного сечения элемента с учетом размещения
анкерных и натяжных устройств на торцах элемента. 5.30. Если при проектировании предусматривается обрыв
арматуры в пределах длины элемента, ее анкеры рекомендуется располагать в зоне
сечения, сжатой от действия внешней нагрузки. В случае
расположения анкеров в зоне, работающей от внешней нагрузки на растяжение,
должна быть предусмотрена постановка арматуры, воспринимающей местные усилия в
сечениях, примыкающих к месту обрыва напрягаемой арматуры. 5.31. При размещении анкеров на арматуре следует учитывать
их перемещение при удлинении арматуры в процессе ее натяжения на упоры или на
бетон; после натяжения арматуры анкер должен занимать проектное положение. Анкеровка ненапрягаемой арматуры5.32 (5.14). Продольные стержни растянутой и сжатой ненапрягаемой арматуры должны
быть заведены за нормальное к продольной оси элемента сечение, в котором они
учитываются с полным расчетным сопротивлением, на длину не менее lan, определяемую по формуле но не менее lan = lan d, где значения wan, Dlan и lan, а также допускаемые
минимальные величины lan определяется по табл. 50, при этом гладкие арматурные стержни должны
оканчиваться крюками или иметь приваренную поперечную арматуру по длине заделки.
Расчетное сопротивление бетона Rb учитывается в формуле (274) при gb2 = 1,0. Для элементов из
мелкозернистого бетона группы Б (см. п. 2.1) значения lan, определяемые по формуле (274),
должны увеличиваться на 10d
для растянутого бетона и на 5d -
для сжатого. В случае, когда
анкеруемые стержни поставлены с запасом по площади сечения против требуемой
расчетом по прочности с полным расчетным сопротивлением, вычисленную по формуле
(274)
длину анкеровки lan допускается уменьшать,
умножая на отношение необходимой по расчету и фактической площадей сечения
арматуры. Если по расчету
вдоль анкеруемых стержней образуются трещины от растяжения бетона, то стержни
должны быть заделаны в сжатую зону бетона на длину lan, определяемую по формуле (274). При
невозможности выполнения указанных выше требований должны быть приняты меры по
анкеровке продольных стержней для обеспечения их работы с полным расчетным
сопротивлением в рассматриваемом сечении (постановка косвенной арматуры,
приварка к концам стержней анкерующих пластин или закладных деталей, отгиб
анкерующих стержней). При этом величина lan должна быть не менее 10d. Таблица 50 (37)
УКАЗАНИЯ ПО АРМИРОВАНИЮ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВПродольное армирование элементов5.33 (5.16). Площадь сечения продольной арматуры в железобетонных
элементах (в процентах площади сечения бетона) должна приниматься не менее
указанной в табл. 51. Требования табл.
51
не распространяются на армирование, определяемое расчетом элемента для стадий
транспортирования и возведения; в этом случае площадь сечения арматуры
определяется только расчетом по прочности. Требования
настоящего пункта не учитываются при назначении площади сечения арматуры,
устанавливаемой по контуру плит или панелей из расчета на изгиб в плоскости
плиты (панели). 5.34 (5.56). Часть продольной стержневой арматуры элемента
допускается применять без предварительного напряжения, если при этом
удовлетворяются требования расчета по трещиностойкости и по деформациям. 5.35 (5.18). В линейных внецентренно сжатых элементах расстояния
между осями стержней продольной арматуры должны приниматься в направлении,
перпендикулярном плоскости изгиба, не более 400 мм, а в направлении плоскости
изгиба - не более 500 мм. Таблица 51 (38)
Примечание. Минимальная площадь сечения арматуры, приведенная в настоящей таблице, относится к площади сечения бетона, равной произведению ширины прямоугольного сечения либо ширины ребра таврового (двутаврового) сечения b на рабочую высоту сечения h0. В элементах с продольной арматурой, расположенной равномерно по контуру сечения, а также в центрально-растянутых элементах минимальная площадь сечения всей продольной арматуры относится к полной площади сечения бетона и принимается вдвое больше величин, указанных в настоящей таблице. 5.36 (5.20,
5.60). В
балках шириной более 150 мм число продольных рабочих стержней, заводимых за
грань опоры, должно быть не менее двух. В ребрах сборных панелей, настилов,
часторебристых перекрытий и т.п. шириной 150 мм и менее допускается доведение
до опоры одного продольного рабочего стержня. В плитах
расстояния между стержнями, заводимыми за грань опоры, не должны превышать 400
мм, причем площадь сечения этих стержней на 1 м ширины плиты должна составлять
не менее 1/3 площади сечения стержней в пролете, определенной расчетом по
наибольшему изгибающему моменту. Напрягаемая
арматура - стержневая или канаты в пустотных и ребристых элементах - должна
располагаться, как правило, по оси каждого ребра элемента, за исключением
предварительно напряженных многопустотных (с круглыми пустотами) плит высотой
300 мм и менее, изготовляемых из тяжелого бетона, в которых расстояние между
напрягаемой арматурой, заводимой за грань опоры, допускается увеличивать до 600
мм, если для сечений, нормальных к продольной оси плиты, величина момента
трещинообразования Mcrc, определяемого по формуле (164), составляет не менее 80 %
величины момента от внешней нагрузки, принимаемой с коэффициентом надежности по
нагрузке gf = 1,0. Расстояние между
осями рабочих стержней в средней части пролета плиты и над опорой (вверху)
должны быть не более 200 мм при толщине плиты до 150 мм и не более 1,5h - при толщине плиты более
150 мм (h - толщина плиты). 5.37 (5.21). В изгибаемых элементах при высоте сечения более 700
мм у боковых граней должны ставиться конструктивные продольные стержни с
расстояниями между ними по высоте не более 400 мм и площадью сечения не менее
0,1 % площади сечения бетона, имеющего размер, равный: по высоте элемента -
расстоянию между этими стержнями, по ширине - половине ширины ребра элемента,
но не более 200 мм. 5.38. Продольную ненапрягаемую арматуру рекомендуется
располагать ближе к наружным поверхностям элемента так, чтобы поперечная
арматура (хомуты) охватывала напрягаемую арматуру. Поперечное армирование элементов5.39 (5.22). У всех поверхностей железобетонных элементов, вблизи
которых ставится продольная арматура, должна предусматриваться также поперечная
арматура, охватывающая крайние продольные стержни. При этом расстояния между
поперечными стержнями у каждой поверхности элемента должны быть не более 600 мм
и не более удвоенной ширины грани элемента. Во внецентренно
сжатых элементах с центрально-расположенной напрягаемой продольной арматурой
(например, в сваях) постановки поперечной арматуры не требуется, если
сопротивление действию поперечных сил обеспечивается одним бетоном. Поперечную
арматуру допускается не ставить у граней тонких ребер изгибаемых элементов
(шириной 150 мм и менее), по ширине которых располагается лишь один продольный
стержень или сварной каркас. Во внецентренно
сжатых линейных элементах, а также в сжатой зоне изгибаемых элементов при
наличии учитываемой в расчете сжатой ненапрягаемой продольной арматуры хомуты
должны ставиться на расстояниях: при Rsc £ 400 МПа - не более 500 мм и
не более: при вязаных каркасах - 15d,
сварных - 20d; при Rsc ³ 450 МПа - не более 400 мм и
не более: при вязаных каркасах - 12d,
сварных - 15d (d - наибольший диаметр
продольных сжатых стержней). При этом
конструкция поперечной арматуры должна обеспечивать закрепление сжатых стержней
от их бокового выпучивания в любом направлении. Вышеуказанные
требования распространяются и на расположенные в сжатой зоне напрягаемые
стержни с напряжениями ssc > 0 (см. п. 3.8); при
этом взамен значения Rsc принимается значение ssc. При проверке
соблюдения требований настоящего пункта продольные сжатые стержни, не
учитываемые расчетом, не должны приниматься во внимание, если диаметр этих
стержней не превышает 12 мм и половины толщины защитного слоя бетона. 5.40 (5.25). Диаметр хомутов в вязаных каркасах внецентренно
сжатых линейных элементов должен приниматься не менее 0,25d и не менее 5 мм (d - наибольший диаметр
продольных стержней). Диаметр
хомутов в вязаных каркасах изгибаемых элементов должен приниматься, мм, не
менее: при высоте сечения элемента, равной или менее 800 мм.............................. 5 то же, св. 800 мм.................................................................................................. 8 Вышеуказанные требования
можно не распространять на спиральную или кольцевую арматуру центрифугированных
трубчатых элементов. Соотношение
диаметров поперечных и продольных стержней в сварных каркасах и в сварных
сетках устанавливается из условия сварки по соответствующим нормативным
документам. 5.41 (5.26). В балочных конструкциях высотой свыше 150 мм, а также в многопустотных
плитах (или аналогичных часторебристых конструкциях) высотой более 300 мм
должна устанавливаться поперечная арматура. В сплошных
плитах независимо от высоты, в многопустотных плитах (или аналогичных
часторебристых конструкциях) высотой 300 мм и менее и в балочных конструкциях
высотой 150 мм и менее допускается поперечную арматуру не устанавливать. При
этом должны быть обеспечены требования расчета согласно п. 3.30. 5.42 (5.27). Поперечная арматура в балочных и плитных
конструкциях, указанных в п. 5.41, устанавливается: на приопорных участках,
равных при равномерно распределенной нагрузке 1/4 пролета, а при
сосредоточенных нагрузках - расстоянию от опоры до ближайшего груза, но не
менее 1/4 пролета, с шагом: при высоте сечения элемента h, равной или менее 450 мм.................................................................................... не более h/2 и не более 150 мм то же, св. 450 мм.................................................................................................. не более h/3 и не более 500 мм На остальной части пролета
при высоте сечения свыше 300 мм устанавливается поперечная арматура с шагом не
более 3/4h и не более 500 мм. 5.43 (5.28). Поперечная арматура, предусматриваемая для восприятия
поперечных сил, должна иметь надежную анкеровку по концам путем приварки в
соответствии с требованиями поз. 1 и 2 обязательного приложения 3 СНиП 2.03.01-84,
обеспечивающую равнопрочность соединений и хомутов или обхвата продольной
арматуры. При этом как в сварных, так и в вязаных каркасах диаметр продольных
стержней должен быть не менее 0,8 диаметра поперечных. 5.44. Отгибание стержневой или проволочной арматуры,
натягиваемой на упоры, может выполняться по дуге окружности диаметром от d до 30d.
При этом следует учитывать снижение прочности арматуры в зоне перегиба (см.
поз. 5 табл. 23).
Угол отгиба рекомендуется принимать не более 45°. Отогнутую
арматуру, натягиваемую на бетон, рекомендуется выполнять с криволинейным
очертанием при угле наклона к продольной оси элемента не более 30° и при радиусе закругления: а) для пучковой арматуры и
канатов: при диаметре проволок в пучках 5 мм и менее и при диаметре канатов 6 -
9 мм - не менее 4 м; при диаметре проволок в пучках 6 - 8 мм и диаметре канатов
12 и 15 мм - не менее 6 м; б) для
стержневой арматуры: диаметром до 25 мм - не менее 15 м, диаметром от 28 до 40
мм - не менее 20 мм. При
осуществлении мер, способствующих уменьшению трения напрягаемой арматуры о
стенки каналов (тефлоновые прокладки, оболочки из синтетических материалов и
др.), могут приниматься меньшие радиусы закругления с соответствующим
экспериментальным обоснованием. 5.45 (5.31). В элементах, работающих на изгиб с кручением,
вязаные хомуты должны быть замкнутыми, с надежной анкеровкой по концам, а при
сварных каркасах все поперечные стержни обоих направлений должны быть приварены
к угловым продольным стержням, образуя замкнутый контур. При этом должна быть
обеспечена равнопрочность соединений и хомутов. Армирование концов предварительно напряженных элементов5.46 (5.61). У концов предварительно напряженных элементов в целях ограничения
развития трещин вдоль напрягаемой арматуры должна быть установлена
дополнительная поперечная или косвенная арматура (сварные сетки, охватывающие
все продольные стержни арматуры, хомуты и т.п. с шагом 5 - 10 см) на длине
участка не менее 0,6lp, а в элементах из легкого бетона классов В7,5 - В12,5 с шагом 5 см -
на длине не менее lp (см. п. 2.26) и не менее 20 см для элементов с арматурой, не имеющей
анкеров, при наличии анкерных устройств - на участке, равном двум длинам этих
устройств (черт. 61 и 62). Концы узких
ребер рекомендуется усиливать путем постановки закладных деталей - обойм с
анкерными стержнями (черт. 63). Эти анкерные стержни можно учитывать при
выполнении требований п. 5.47. Черт. 61. Армирование конца предварительно напряженной балки 1 - сварные сетки в виде гребенок (для удобства укладки напрягаемых стержней), требуемые согласно п. 5.46; 2 - поперечные стержни, требуемые согласно п. 5.47 и привариваемые к закладной детали; 3 - напрягаемая арматура (основная поперечная арматура балок и арматура, установленная по контуру опорного уширения, не показана) Черт. 62. Армирование конца многопустотного настила 1 - сварная сетка, требуемая согласно п. 5.46; 2 - напрягаемые стержни Черт. 63. Армирование конца ребра плиты перекрытия 1 - сварная сетка согласно п. 5.46; 2 - плоский арматурный каркас ребра; 3 - анкерные стержни закладной детали - обоймы согласно пп. 5.46 и 5.47; 4 - напрягаемый стержень (арматура полки плиты и поперечного ребра, а также арматура в углах между поперечными и продольным ребрами не показана) Для элементов с
арматурой, имеющей внутренние анкеры, указанная поперечная арматура может
учитываться в расчете по прочности. Для элементов
со стержневой напрягаемой арматурой при передаточной прочности бетона не менее
22 МПа указанную поперечную или косвенную арматуру можно не устанавливать,
если: при d = 10 - 14 мм ssp £ 460 МПа; при d = 16 - 20 мм ssp £ 420 МПа; при d = 22 - 32 мм ssp £ 380 МПа (напряжение ssp принимается с учетом потерь
по поз. 1 - 5 табл. 4 при gsp = 1,0; d -
диаметр напрягаемой арматуры). В случае
отсутствия по длине элемента поперечной или косвенной арматуры указанные
значения ssp снижается на 40 МПа. При
многозвенной передаче усилия на бетон указанные значения ssp снижаются на 15 %. При передаточной
прочности бетона менее 22 МПа дополнительную поперечную или косвенную арматуру
можно не устанавливать лишь при ssp £ 260 МПа. 5.47 (5.58). Для предотвращения образования продольных трещин у торцов
предварительно напряженных изгибаемых элементов вследствие передачи усилий
напрягаемой арматуры на бетон рекомендуется отгибание части продольной
напрягаемой арматуры у опор элемента и распределение ее на торце равномерно по
высоте; при этом часть отогнутой арматуры допускается выводить на верхнюю грань
элемента. Если напрягаемая
продольная арматура располагается сосредоточенно у нижней или у нижней и
верхней граней элемента, у торцов необходимо предусматривать дополнительную
напрягаемую или ненапрягаемую поперечную арматуру, располагая ее на участке
длиной не более 1/4 высоты элемента. Напрягаемая
поперечная арматура должна напрягаться ранее натяжения продольной арматуры
усилием не менее 15 % усилия натяжения всей продольной арматуры растянутой зоны
опорного сечения. Ненапрягаемая
поперечная арматура должна быть надежно заанкерена по концам приваркой к закладным
деталям. Сечения этой арматуры в конструкциях, не рассчитываемых на
выносливость, должно быть в состоянии воспринимать не менее 20 %, а в
конструкциях, рассчитываемых на выносливость, - не менее 30 % усилия в
продольной напрягаемой арматуре нижней зоны опорного сечения, определяемого
расчетом по прочности (т.е. равного Rs Asp). Допускается
также применять приопорную поперечную арматуру в виде корытообразных сеток,
охватывающих нижнюю продольную арматуру. 5.48 (5.57). Местное усиление участков предварительно напряженных
элементов под анкерами напрягаемой арматуры, а также в местах опирания натяжных
устройств рекомендуется выполнять установкой закладных деталей или
дополнительной поперечной арматуры и увеличением размеров сечения элемента на
этих участках. Сварные
соединения арматуры
5.49 (5.32). Арматура из горячекатаной стали гладкого и
периодического профилей, термически упрочненной стали классов Ат-IIIC и
Ат-IVC и обыкновенной арматурной проволоки, а также закладные детали должны,
как правило, изготовляться с применением для соединения стержней между собой и
с плоскими элементами проката контактной сварки - точечной и стыковой.
Допускается применение дуговой сварки - автоматической и полуавтоматической, а
также ручной согласно указаниям п. 5.53. Стыковые соединения
упрочненной вытяжкой арматуры класса А-IIIв должны свариваться до ее
упрочнения. Сварные
соединения стержневой термически упрочненной арматуры классов АТ-V и Ат-VI,
высокопрочной арматурной проволоки и арматурных канатов не допускаются. 5.50 (5.33). Типы сварных соединений и способы сварки арматуры и
закладных деталей должны назначаться с учетом условий эксплуатации и
свариваемости стали, технико-экономических показателей и технологических возможностей
предприятия-изготовителя в соответствии с указаниями государственных стандартов
и нормативных документов на сварную арматуру и закладные детали железобетонных
конструкций (см. обязательные приложения 3 и 4
СНиП 2.03.01-84). 5.51 (5.34). В заводских условиях при изготовлении сварных
арматурных сеток, каркасов и соединений по длине отдельных стержней следует
применять преимущественно контактную точечную и стыковую сварку, а при изготовлении
закладных деталей - автоматическую сварку под флюсом для тавровых и контактную
рельефную сварку для нахлесточных соединений. Конструирование
сварных каркасов, сеток и закладных деталей рекомендуется производить в
соответствии с указаниями «Пособия по проектированию бетонных и железобетонных
конструкций из тяжелых и легких бетонов без предварительного напряжения
арматуры». 5.52 (5.35). При монтаже арматурных изделий и сборных
железобетонных конструкций в первую очередь должны применяться полуавтоматические
способы сварки, обеспечивающие возможность контроля качества соединений. 5.53 (5.36). При отсутствии необходимого сварочного оборудования допускается
выполнять в заводских и монтажных условиях крестообразные, стыковые,
нахлесточные и тавровые соединения арматуры и закладных деталей, применяя
приведенные в обязательных приложениях 3 и 4 СНиП 2.03.01-84 и в нормативных документах
на сварную арматуру и закладные детали способы дуговой, в том числе и ручной,
сварки. Применяя ручную
дуговую сварку при выполнении сварных соединений, рассчитываемых по прочности,
в сетках и каркасах, следует устанавливать дополнительные конструктивные
элементы в местах соединения стержней продольной и поперечной арматуры
(прокладки, косынки, крючки и т.д.). Отдельные
указания по конструированию
5.54 (5.52). В элементах сборных конструкций должны
предусматриваться приспособления для захвата их при подъеме: инвентарные
монтажные вывинчивающиеся петли, строповочные отверстия со стальными трубками,
стационарные монтажные петли из арматурных стержней и т.п. Петли для подъема
должны выполняться из горячекатной стали согласно требованиям п. 2.21, а также
«Пособия по проектированию бетонных и железобетонных конструкций из тяжелых и
легких бетонов без предварительного напряжения арматуры». 5.55. В целях снижения отрицательного воздействия
предварительного напряжения, вызванного образованием начальных трещин в верхней
зоне балок, плит и т.п., рекомендуется назначать места расположения
строповочных устройств и места опирания при перевозке максимально приближенными
к концам элемента с учетом возможностей подъемных механизмов, применяемых
траверс, транспортных средств. Места опирания при хранении элемента
рекомендуется назначать на расстоянии не более 20 - 30 см от его концов. 5.56 (5.50). Отверстия значительных размеров в железобетонных
плитах, панелях и т.п. должны окаймляться дополнительной арматурой сечением не
менее сечения рабочей арматуры (того же направления), которая требуется по
расчету плиты как сплошной. Небольшие
отверстия в железобетонных элементах для коммуникаций, строповки и т.п. следует
располагать в пределах ячеек арматурных сеток и каркасов так, чтобы не
перерезать арматуру и не вводить дополнительное местное армирование. Углы
отверстий желательно делать плавными (см. черт. 56, г). Обрамление
отверстий стальными закладными деталями замкнутой формы, особенно с острыми
углами, не рекомендуется во избежание образования трещин в бетоне вследствие
его усадки. 5.57. При натяжении арматуры на бетон в местах резкого
изменения кривизны каналов для пропуска арматуры следует устанавливать отрезки
жестких стальных труб. Канал для нескольких пучков или стержней должен иметь на
концах уширения для анкерных и натяжных устройств. В местах перегиба арматуры
(черт. 64)
или уширения канала необходимо усиливать бетон стальными обоймами, хомутами или
сетками, а также при необходимости увеличивать сечение элемента. Черт. 64.
Усиление бетона дополнительным армированием в местах перегиба напрягаемой
арматуры ПРИЛОЖЕНИЕ 1КОМПЛЕКСНЫЙ ПРИМЕР РАСЧЕТА БАЛКИ ПОКРЫТИЯДано: предварительно напряженная балка покрытия с
параллельными поясами сечением по черт. 1 загружена сосредоточенными
силами по черт. 2,
а; длина балки 12 м; расчетный пролет l = 11,7 м; монтажные петли - на расстоянии l1 = 1,5 м от торцов балки; прокладки при
складировании ставятся у концов элемента. Балка из
тяжелого бетона класса В40 (Rb = 22 МПа и Rbt = 1,4 МПа при gb2
= 1,0, Rb,ser = 29 МПа, Rbt,ser = 2,1 МПа, Eb = 3,25 × 104 МПа);
передаточная прочность бетона Rbp = 25 МПа (Rb(p) = 14,5 МПа, Черт. 1. Поперечное сечение балки Продольная
арматура в растянутой от внешних нагрузок зоне класса К-7, диаметром 15 мм (Rs = 1080 МПа, Rs,ser = 1295 МПа, Es = 1,8 × 105 МПа); ее площадь Asp = 1132 мм2 (8 Æ 15); анкеры на концах
арматуры отсутствуют; натяжение арматуры производится механическим способом на
упоры стенда с применением инвентарных зажимов. В сжатой (верхней) зоне
продольная арматура диаметром 16 мм, класса А-III (Rs = Rsc = 365 МПа, Rs,ser = 390 МПа, Es = 2 × 106 МПа); ее площадь A¢s
= 402 мм2 (2 Æ 16); поперечная арматура
класса А-III, площадью Asw = 50,3 мм2 (1 Æ 8) (Rsw = 285 МПа), шагом s =
150 мм. Нагрузка от
собственного веса балки при коэффициенте надежности по нагрузке gf
= 1,0 qw = 3800 Н/м; момент в
середине пролета от всех нагрузок при gf > 1,0: MII = 703 кН · м, то же, от
всех нагрузок, кроме крановой нагрузки, MI = 649 кН · м. Момент в
середине пролета от всех нагрузок при gf = 1,0 Mtot = 560 кН · м, то же, от постоянных и длительных нагрузок Ml = 475 кН · м; эпюры
поперечных сил от всех нагрузок при gf > 1,0 по черт. 2, б,
то же, без учета крановой нагрузки - по черт. 2, в, то же, от всех
нагрузок при gf = 1,0 - по черт. 2, г. Балка
эксплуатируется в слабоагрессивной среде. Конструктивные и технологические
требования к прогибу балки отсутствуют. Черт. 2. Эпюры поперечных сил балки покрытия а - схема загружения балки (значение сил в скобках - при gf = 1,0); б - эпюра Q от всех нагрузок при gf > 1,0; в - то же, от всех нагрузок, кроме крановой; г - то же, от всех нагрузок при gf = 1,0 Требуется рассчитать балку по всем предельным состояниям. РАСЧЕТ I. Определение геометрических характеристик приведенного сечения Геометрические
характеристики определяем согласно указаниям п. 1.21:
+ 4 × 0,5 × 100 × 100 + 5,55 × 1132 + 6,15 × 402 = 154000 мм2;
II. Определение усилия
предварительного обжатия P и эксцентриситета e0p Величину
предварительного напряжения арматуры ssp без учета потерь принимаем максимально допускаемой: ssp = 0,95Rs,ser = 0,95 × 1295 = 1230 МПа. Усилие P определяем в трех
характерных сечениях по длине балки: в середине пролета, на конце длины зоны
передачи напряжений lp и в месте установки монтажных петель. 1. Сечение в середине пролета. Определяем потери предварительного напряжения в
арматуре согласно табл. 4: а) первые потери
s2 = 1,25Dt = 1,25 × 65 = 81 МПа (Dt принято равным 65 °C, так как отсутствуют точные
данные о величине температурного перепада);
(Dl = 1,25 + 0,15d = 1,25 + 0,15 × 15 = 3,5 мм); s4 = 0 (трение арматуры при ее
натяжении отсутствует); s5 = 0 (натяжение производится
на упор стенда). Определяем
предварительное напряжение s0I
и усилие PI,
вычисленные с учетом потерь от s1 до s5: sspI = ssp - s1 - s2 - s3 = 1230 - 134 - 81 - 42 = 973 МПа; PI = sspI Asp = 973 × 1132 = 1104 × 103 H. Эксцентриситет
усилия PI
равен e0p = ysp = 426 - 72,5 = 353,5 мм. Для определения потерь от быстронатекающей
ползучести находим по формуле (10) напряжение в бетоне sbp на уровне центра тяжести арматуры S (т.е. при y = ysp = 353,5 мм), принимая момент от собственного веса балки равным:
Согласно поз. 6 табл. 4, a = 0,25 + 0,025Rbp = 0,25 + 0,025 × 25 = 0,875 > 0,8, принимаем a = 0,8. Так как
Аналогично
определяем потери от быстронатекающей ползучести на уровне центра тяжести
арматуры S′, принимая y = y′s = 845 - 426 = 419 мм:
т.е. на этом уровне
напряжение в бетоне растягивающее, поэтому s6 = 0, а следовательно, s′s
= 0. В соответствии с
этим напряжение ssp1
учетом первых потерь и соответствующее усилие обжатия равны: ssp1 = sspI - s6 = 973 - 20,1 = 952,9 МПа; P1 = ssp1 Asp =
953 × 1132 = 1078,8 кН. Поскольку s′s
= 0, эксцентриситет усилия P1 не меняется, т.е. e0p
= ysp = 353,5 мм; б) вторые потери (по поз. 8 и 9 табл. 4): s8 = 40 МПа; для определения
потерь s9 оставляем прежнее отношение
ssp2 = ssp1 - s8 - s9 = 952,9 - 40 - 75,5 = 837,4 МПа. Поскольку напряжение в
бетоне на уровне арматуры S′ остается растягивающим, s′s = 0, тогда: P2 = ssp2 Asp = 837,4 × 1132 = 947,9 × 103
H = 947,9 кН; e0p = ysp = 353,5 мм. 2. Сечение в конце зоны передачи напряжений длиной lp. Поскольку потери напряжений s1 - s5 не зависят от места
расположения сечения по длине элемента, то sspI
и PI
в рассматриваемом сечении такие же, как и в середине пролета, т.е. ssp1 = 973 МПа, PI = 1101 кН. Длину зоны
передачи напряжений определяем согласно п. 2.26. Поскольку Rs = 1080 МПа > ssp1 = 973 МПа, принимаем stp = Rs = 1080 МПа. Из табл. 24 при арматуре
класса К-7 и d = 15 мм имеем wp = 1,0, lp = 25. Тогда
Аналогично
определим потери напряжений s6 и s9:
где х = 1,023 - 0,13 = 0,893 м (см. черт. 2);
Так как Так как Определяем ssp2 при s8 = 40 МПа: ssp2 = ssp1 - s6 - s8 - s9 = 973 - 21,55 - 40 - 81,15 = 830,2 МПа. Поскольку момент
от собственного веса, сжимающий верхнюю грань, меньше, чем для сечения в
середине пролета, бетон на уровне верхней арматуры будет заведомо растянут,
отсюда s′s = 0 и тогда: P2 = ssp2 Asp = 830,2 × 1132 = 939,9 кН; e0p = ysp = 353,5 мм. 3. Сечение в месте установки монтажной петли. Расчет производим
аналогично предыдущему расчету, вводя момент от собственного веса, равный:
где х = 1,5 - 0,13 = 1,37 м;
Отсюда ssp1 = sspI
- s6 = 973 - 21,9 = 951,1 МПа; P1 = ssp1 Asp = 951,1 × 1132 = 1076,6 кН. Усилие обжатия с
учетом всех потерь P2 для этого сечения не
определяем, поскольку в стадии эксплуатации это сечение не является опасным. 4. Проверка сжимающих напряжений sbp. Наибольшие сжимающие
напряжения sbp имеют место в сечении,
проходящем через конец приопорной зоны длиной lp, поскольку здесь разгружающее влияние момента Mw наименьшее. Напряжение sbp определяем на уровне
крайнего нижнего волокна (т.е. при y = y0 = 426 мм) при действии усилия P1 с учетом первых потерь,
равного P1 = (sspI - s6) Asp = (973 - 21,55) 1132 = 1077
кН:
что меньше предельно
допустимого значения III. Расчет по прочности в
стадии изготовления От воздействия
усилия P1 верхняя зона балки
растянута, нижняя сжата. В соответствии с этим в данном расчете As = 402 мм2; A′sp = 1132 мм2; a = 45 мм; b′f = 280 мм; Расчет
производим, согласно пп. 3.44 - 3.48, для сечения в месте установки монтажной
петли, поскольку в этом сечении момент усилия обжатия и момент от собственного
веса при подъеме балки растягивают верхнюю зону, т.е. эти моменты суммируются. Для этого
сечения ssp1 = 951,1 МПа (см. п. II, 3).
Поскольку способ натяжения механический, коэффициент точности натяжения
принимаем равным gsp = 1 + Dgsp = 1 + 0,1 = 1,1, т.е. ssp1 = 1,1 × 951,1 = 1046 МПа. Тогда Np = (ssp - 330) A′sp = (1046 - 330) 1132 = 310750 Н. Расчетное сопротивление бетона
принимаем по передаточной прочности бетона Rbp = 25 МПа с учетом коэффициента gb8 = 1,1 (см. поз. 5 табл. 14), т.е. Так как Площадь сечения сжатых
свесов равна: Aov = (b′f
- b) h′f
= (280 - 80) 200 = 40000 мм2;
Так как Определим момент
при подъеме балки, учитывая коэффициент динамичности 1,4 и коэффициент gf = 1,1:
Тогда
т.е. прочность сечения
обеспечена. IV. Расчет по прочности
нормальных сечений в стадии эксплуатации Расчет
производим для сечения в середине пролета. Так как MI = 649 кН · м > 0,82MII
= 0,82 × 703 = 576,5 кН · м,
согласно п. 3.1., расчет выполняем при расчетном сопротивлении бетона Rb (при gb1 = 1,0), умноженном на коэффициент Из черт. 1 имеем: h0 = h - а = 890 - 72,5 =
817,5 мм;
b′f = 280 мм; b = 80 мм. Проверим условие (37) п. 3.13 при gs6 = 1,0:
т.е. граница сжатой зоны
проходит в ребре, и прочность сечения проверяем согласно п. 3.13б:
Из табл. 26 при gb2 = 1,0, классе арматуры К-7 и Так как x1 = 0,247 < xR = 0,38, определяем коэффициент gs6 по формуле (41), вычисляя
и h = 1,15:
Высота сжатой
зоны равна:
Прочность
сечения проверяем из условия (39):
т.е. прочность нормального
сечения обеспечена. V. Расчет по прочности
наклонных сечений 1. Проверка прочности наклонной полосы между наклонными трещинами в
стенке балки. Расчет
ведем согласно п. 3.21. Поскольку для сечения у опоры (см. черт. 2, б и в)
Q1 = 172,3 кН < 0,82QII
= 0,82 × 211,9 = 173,6 кН, согласно
п. 3.1, расчетное сопротивление бетона Rb принимаем с учетом коэффициента gb2 = 1,1 (т.е. Rb = 24 МПа) и расчет ведем на действие силы QII
= 211,9 кН (уменьшением Q на
расстоянии h0 от опоры пренебрегаем):
jw1 = 1 + 5amw = 1 + 5 × 5,54 × 0,00419 = 1,116; b = 0,01 (так как бетон
тяжелый); jb1 = 1 - b Rb = 1 - 0,01 × 24 = 0,76; 0,3jw1 jb1 Rb
bh0 = 0,3 × 1,116 × 0,76 × 24 × 80 × 817,5 = = 399,4 × 103 Н > QII
= 211,9 кН, т.е. прочность сжатого
бетона стенки обеспечена. 2. Проверка прочности наклонных сечений на действие поперечной силы. Проверим наклонное сечение с
длиной проекции, равной расстоянию от опоры до первого груза - с1
= 1,35 м (см. черт. 2, а).
Для этого сечения QI = 167 кН < 0,82QII = 0,82 × 206,5 = 169,3 кН, т.е.
расчетное сопротивление бетона также принимаем с учетом коэффициента gb2
= 1,1 - Rbt = 1,55 МПа, и расчет
выполняем на действие силы QII = 206,5 кН. Из черт. 1 имеем b′f
- b = 280 - 80 = 200 мм < 3h′f
= 3 × 170 = 510 мм, т.е. свесы
учитываем полностью. Определим
значения Mb и Qb: jb2 = 2,0 (поскольку бетон
тяжелый);
P = 939,9 кН (см. п. II, 2), с учетом gsp = 0,9 P =
0,9 × 939,9 = 845,9 кН;
Принимаем jn = 0,5. Поскольку 1 + jf + jn > 1,5, принимаем 1 + jf + jn = 1,5; Mb = jb2 (1 + jf + jn) Rbt bh20 = 2 × 1,5 × 1,55 × 80 × 817,52 = 248,6 × 106 Н · мм;
Значение qsw равно:
т.е. условие (79)
выполняется и значение Mb не корректируется;
Так как с0 = 1,6 м > с1
= 1,35 м, принимаем с0 = с1 = 1,35 м
< 2h0 = 2 × 0,8177 = 1,635 м. Проверяем
условие прочности наклонного сечения: Qb + qsw c0 = 184,1 × 103 + 95,6 × 1350 = 313,2 × 103 H > QII
= 206,5 кН, т.е. прочность этого
наклонного сечения обеспечена. Проверяем
наклонное сечение с длиной проекции, равной расстоянию от опоры до второго
груза:
Принимаем с2 = 2,72 м. Для этого
сечения QI
= QII
= 161 кН, т.е. крановая нагрузка не влияет на Q, и, следовательно, расчетное сопротивление бетона принимаем с учетом
коэффициента gb2 = 0,9, Rbt = 1,25 МПа. Поскольку
коэффициенты jb2 и 1 + jf + jn не изменились, уточним только значения Mb и Qb:
Тогда Так как с0 =
1,448 м < c2 = 2,85 м и с0 < 2h0 = 1,635 м, оставляем с0 =
1,448 м; Qb + qw c0 = 73,7 × 103 + 95,6 × 1448 = 208,8 × 103 Н > QI
= 161 кН, т.е. прочность любых
наклонных сечений по поперечной силе обеспечена. 3. Проверка прочности наклонных сечений на действие изгибающего момента. Поскольку продольная
арматура не имеет по концам специальных анкеров, такая проверка необходима. При
этом предполагаем, что условия п. 3.30 не выполняются. Расчет производится
согласно пп. 3.31 и 3.33. Начало наклонного
сечения принимаем у грани опоры, т.е. на расстоянии lx = 130 + 140 = 270 мм от торца балки. Из п. II, 2 имеем lp = 1023 мм. Поскольку lx < lp, расчетное сопротивление
продольной арматуры Rs определяем с учетом коэффициента
Тогда zs = h0 - 0,5x = 817,5 - 0,5 × 52,4 = 791,3 мм. Определим длину
проекции невыгоднейшего наклонного сечения по формуле (99), принимая, что в
пределах этого сечения находится только первый груз FI = 39,5 кН, а q = qw = 3,8 × 1,1 = 4,18 кН/м:
при этом с < 2,85 м, т.е. действительно первый
груз находится в пределах наклонного сечения, а второй - вне его. Расчетный момент
определяем в нормальном сечении, проходящем через конец наклонного сечения,
т.е. на расстоянии 1,73 + 0,14 = 1,87 м от точки приложения опорной реакции
(см. черт. 2,
а):
Проверяем условие прочности: Rs Asp zs + 0,5qsw c2
= 285 × 1132 × 791,3 + 0,5 × 95,6 × 17302 = = 398,35 × 106 Н · мм > M = 368,4 кН · м, т.е. прочность наклонных
сечений по моменту обеспечена. VI. Расчет по образованию
нормальных трещин Рассмотрим
сечение в середине пролета. Так как нижняя (растянутая) зона балки армирована
канатами класса К-7 при диаметре проволоки 15/3 = 5 мм > 3 мм, а балка
эксплуатируется в слабоагрессивной среде, то, согласно табл. 9 СНиП 2.03.11-85, к этой
зоне предъявляются требования по трещиностойкости 2-й категории. Поэтому,
согласно табл. 2,
расчет производим на действие момента MII = 703 кН · м; при этом
усилие обжатия вводится с коэффициентом точности натяжения gsp < 1,0. Согласно п. 1.18, gsp = 1 - Dgsp = 1 - 0,1 = 0,9. Сначала проверим
образование в этом сечении начальных (верхних) трещин в стадии изготовления
согласно п. 4.5,
используя тот же коэффициент gsp, что и при проверке нижних
трещин, т.е. gsp = 0,9. Согласно п. II, 1а, имеем P1 = 1078,8 кН, а с учетом gsp - P1 = 0,9 × 1078,8 = 970,9 кН и e0p = ysp = 353,5 мм. Поскольку момент
от собственного веса балки в этом сечении сжимает верхнюю грань, определим его минимальное
значение, т.е. при подъеме балки без учета коэффициента динамичности:
где l2 = l - 2l1 = 12 - 2 × 1,5 = 9 м. Моменты
сопротивления сечения соответственно для нижнего и верхнего волокон равны:
Максимальное напряжение
бетона в стадии изготовления
Из табл. 38 при Проверяем условие (178),
принимая Mr = Mw = 34,2 кН · м:
т.е. верхние трещины в
середине пролета образуются, и, следовательно, значение момента Mcrc определяем с учетом
коэффициента q:
Поскольку
напрягаемая арматура проволочная, снижаем d на 15 %, т.е. d = 0,678 × 0,85 = 0,576 < 1,4; q = 1 - (1,5 - 0,9/d) (1 - jm) = 1 - (1,5 - 0,9/0,576) (1
- 0,527) = 1,03 > 1,0. Принимаем q = 1,0, т.е. влияние верхних
трещин не учитывается. Согласно пп. 4.2 и 4.3,
определим момент сопротивления сечения относительно нижнего волокна Из табл. 38 при Тогда Согласно п. II, 1б, имеем Р2
= 947,9 кН, а с учетом gsp = 0,9 - Р2
= 0,9 × 947,9 = 853,1 кН и е0p = 353,5. Максимальное
напряжение в бетоне в стадии эксплуатации при М = 703 кН · м
Тогда Мrp = Р2 (e0p + rsup) = 853,1 × 103 (353,5 +
225,6) = 494,1 × 106 Н · мм. Вычисляем
значение Мcrc: Мcrc = q (Rbt,ser = 111,4 + 494,1 = 605,5 кН ·
м < MII
= 703 кН · м, т.е. нижние трещины
образуются, и поэтому при действии постоянных и длительных нагрузок требуется
проверка по их закрытию, а при действии всех нагрузок - проверка ширины их
раскрытия. Поскольку
верхние трещины в середине пролета образуются в стадии изготовления, они тем
более образуются в месте монтажных петель при подъеме, поэтому в этом сечении
необходима проверка ширины раскрытия трещин. VII. Расчет по раскрытию
нормальных трещин в стадии эксплуатации Поскольку
требования к трещиностойкости нижней зоны балки 2-й категории, ширина раскрытия
нормальных трещин определяется от непродолжительного действия всех нагрузок при
коэффициентах gf = 1,0 и gsp = 1,0. Момент в середине пролета от таких нагрузок
равен 560 кН · м. Согласно п. II, 1б, Р2
= 947,9 кН. Поскольку q = 1 (см. п. VI), оставляем Р2 = 947,9 кН. Определим
значение Мrp, принимая j = 1, т.е. Мrp = Р2 (e0p + rsup) = 947,9 (0,3535 + 0,23) =
552,7 кН · м. Тогда при Rbt,ser Мcrc = 111,4 + 552,7 = 664,1 кН · м
> Мtot = 560 кН · м, следовательно, значение ss определяем по формуле (208), вычисляя ss,crc с заменой М на Mrp = 552,7 кН · м. Так как 350Asp = 350 × 1132 = 396 × 103 H < P2 = 947,9 кН, значение ss,crc определим по упрощенной формуле (209).
При этом, поскольку e0p = ysp, esp = 0 и тогда Ms = Mcrc = 664,1 кН · м:
Для определения
коэффициента jcrc по табл. 40 принимаем ближайшие
табличные значения: jf = 0,5, ma = 0,1, тогда при
Тогда, принимая Мr = Mtot = 560 кН · м, имеем
Для определения ss на уровне нижнего ряда растянутой
арматуры находим коэффициент dn, принимая х
= 0,5h0 = 0,5 × 817,5 = 410 мм, а2 = 50 мм:
ss = 4,03 × 1,055 = 4,25 МПа. Принимая размеры нижней
полки равными bf = 280 мм и hf = 150 + 100/2 = 200 мм,
определим:
d = 1,0; jl = 1,0; h = 1,2 (как для арматуры
класса К-7), d = 15 мм;
что меньше допускаемого
значения аcrc1 = 0,1 мм (см. табл. 9 СНиП 2.03.11-85). VIII. Расчет по закрытию
нормальных трещин Проверяем
условие (218)
при действии постоянных и длительных нагрузок при коэффициенте gf = 1,0. Момент в середине
пролета от этих нагрузок равен М = Мl = 475 кН · м. Усилие
обжатия Р2 принимаем с
учетом коэффициента gsp = 0,90, т.е. Р2
= 853,1 кН (см. п. VI). Поскольку 1,1q > 1,0, оставляем Р2 = 853,1 кН. Значение r принимаем равным rsup = 230 мм из п. VII, так как j = 1; при этом Wred = 35,36 × 103 мм3;
e0p = ysp = 353,5 мм; Р2 (e0p + r) - 0,5Wred = 853,1 × 103 (353,5 +
230) - 0,5 × 35,36 × 106 = 479,8 × 106 Н · мм > M = 475 кН · м, т.е. условие
(218)
выполняется. Это означает, что напряжения сжатия на нижней грани балки более
0,5 МПа. Проверяем
условие (217)
при действии всех нагрузок при коэффициентах gf = 1,0 и gsp = 1,0. Тогда для сечения в середине пролета имеем ssp2 = 837,4 МПа (см. п. II, 1б) и ss = 4,25 МПа (см. п. VII). Поскольку q = 1, оставляем ssp2 = 837,4 МПа: ssp2 + ss = 837,4 + 4,25 = 841,7 МПа £ 0,8Rs,ser = 0,8 × 1295 = 1036 МПа, т.е. условие (217)
тоже выполняется, что означает отсутствие необратимых деформаций в арматуре. Таким образом,
при действии постоянных и длительных нагрузок трещины в нижней зоне надежно
закрыты. IX. Расчет по раскрытию трещин
в стадии изготовления Расчет
производим для сечения в месте расположения монтажной петли. Согласно п. III, для этого сечения имеем: As = 402 мм2 (2 Æ 16), A¢sp = 1132 мм2; bf = b¢f = 280 мм; h¢f = 200 мм; hf = 170 мм; а¢р = 72,5 мм; h0 = 845 мм. Расчет ведем на
действие усилия обжатия Р1
при gsp = 1,0 т.е. Р1 = 1076,6 кН (см. п. II, 3) и на действие момента от собственного веса плиты при
подъеме:
Определяем
напряжение в верхней арматуре, вычислив:
esp = e0p + h0 - y0 = 353,5 + 845 - 426 = 772,5 мм; Ms = P1 esp + Mw = 1076,6 × 103 × 772,5 + 5,98 × 106 = 837,7 × 106 Н · мм;
Отсюда
Определим ширину
раскрытия верхних трещин, принимая d = 1,0, jl = 1,0, h = 1,0 и d =
16 мм:
что меньше предельно
допустимого значения acrc1
= 0,4 мм. В том же сечении определим глубину верхних трещин, приняв
hcrc = h - (1,2 + jm) xh0 = 890 - (1,2 + 0,356) 0,435
× 845 = 318 мм, что меньше
0,5h = 0,5 × 890 = 445 мм. X. Расчет по образованию
наклонных трещин Для проверки
отсутствия трещин в пределах зоны передачи напряжений в соответствии с п. 1.11
проверим образование наклонных трещин на уровне центра тяжести сечения как наиболее
опасном. При этом учитываем все нагрузки при gf = 1,0 (см. черт. 2, г) и усилие обжатия Р2 при gsp = 0,9. Уточним длину lp, определенную в п. II, 2, принимая sst = sspI
= 973 МПа:
Усилие Р2 в конце длины зоны
передачи напряжений, согласно п. II, 2, равно Р2 = 939,9 кН, а с учетом gsp = 0,9 - Р2 = 0,9 × 939,9 = 845,9 кН. Рассмотрим
поперечные сечения на границе опорного уширения (сечение I
- I, см. черт. 2) и в конце длины зоны передачи
напряжения lp (сечение II
- II). Сечение I - I. Это сечение
отстоит от торца балки на расстоянии lx = 450 мм. Тогда
Напряжение sх на уровне центра тяжести сечения, т.е. при у = 0, равно:
Определим напряжение sy,loc от местного действия опорной реакции F = Qmax = 169,3 кН: х = 450 - 130 = 320 мм (см.
черт. 2,
а); у = у0 = 426 мм;
Из табл. 39 находим
jy = 0,314. Тогда Поперечная сила в сечении I - I равна:
Определяем главные
растягивающие и сжимающие напряжения:
smt = - 1,66 + 3,41 = 1,75 МПа; smc = 1,66 + 3,41 = 5,07 МПа; ab = 0,01; ab B = 0,01 × 40 = 0,4 > 0,3;
Принимаем gb4 = 1,0. Тогда gb4 Rbt,ser = 2,1 МПа > smt = 1,75 МПа, т.е. наклонные
трещины не образуются. Сечение II - II. Производим
аналогичный расчет. В этом сечении lx = lp и, следовательно, Р2 = 845,9 кН:
Расстояние
сечения II - II от первого груза равно х = 959 - 130 = 829 мм > 0,7h = 0,7 × 890 = 623 мм,
следовательно, не учитываем местное действие опорной реакции. Расстояние
сечения II - II от первого груза равно х = 1350 - 829 = 521 мм < 0,7h = 623 мм, следовательно,
учитываем местное действие первого груза F1 = 32,7 кН, у
= h - y0 = 890 - 426 = 464 мм;
Из табл. 39
находим jу = 0,05. Тогда
Поперечная сила в сечении II - II равна:
smt = - 2,76 + 4,24 = 1,48 МПа;
smc = 2,76 + 4,24 = 7 МПа;
Тогда gb4 Rbt,ser = 2,1 МПа > smt = 1,48 МПа, т.е. трещины не
образуются. Таким образом, в
пределах длины передачи напряжений трещины не образуются, что обеспечивает
надежную анкеровку напрягаемой арматуры. Поскольку стенка
балки армирована только поперечной арматурой класса А-III, к ней предъявляются
требования по трещиностойкости 3-й категории, и, следовательно, расчет по
раскрытию наклонных трещин производится лишь при образовании наклонных трещин
от действия всех нагрузок при gf = 1,0 и усилия обжатия Р при gsp = 1,0. В данном случае при действии таких нагрузок
наклонные трещины будут отсутствовать не только в пределах зоны передачи
напряжений, но и во всей балке, так как в более удаленных от опоры сечениях
значения Q, а следовательно, и tху и smt будут меньшими, чем в сечении II - II. Таким образом, расчет по
раскрытию наклонных трещин не производим. XI. Расчет по деформациям Поскольку момент
в середине пролета от всех нагрузок при gf = 1,0, равный Mtot = 560 кН · м, не превышает момента Mcrc = 664 кН · м, определенного
в пп. VII при gsp = 1,0, кривизны определяем как для сплошного тела. Поскольку прогиб
балки ограничивается только эстетическими требованиями, расчет производим на
действие постоянных и длительных нагрузок при gf = 1,0. Момент в середине пролета от таких нагрузок
равен Ml = 475
кН · м. Принимая jb2 = 2,0 (см. табл. 41), jb1 = 0,85, усилие обжатия (из
п. II, 2, б)
при gsp = 1 равным Р2 = 947,9 кН и e0p = 353,5 мм, определим
кривизны
Согласно п. II, 1а и б, определим ssb = s6 + s8 + s9 = 21 + 40 + 75,5 = 136,5
МПа и s¢sb = s¢s = 0. Тогда
В связи с
образованием в сжатой зоне начальных трещин (см. п. VI) кривизны
при этом, поскольку Полная кривизна
в середине пролета балки равна:
= 0,065 × 10-5 1/мм. Условно принимая
всю нагрузку как равномерно распределенную (rm =
Поскольку l/h = 11,7/0,89 = 13,1 > 10, влияние деформаций сдвига не учитываем.
Предельно допустимый прогиб для балок покрытия равен ПРИЛОЖЕНИЕ 2СОРТАМЕНТ АРМАТУРЫТаблица 1
Примечание: 1. Номинальный диаметр стержней для арматуры периодического профиля соответствует номинальному диаметру равновеликих по площади поперечного сечения гладких стержней. 2. Знак «+» определяет наличие диаметра в сортаменте; диапазоны диаметров для различных классов стержневой арматуры и проволоки приведены в табл. 17. 3. Для проволоки класса Вр-I теоретическая масса 1 м при диаметрах 3, 4 и 5 мм принимается соответственно равной 0,052, 0,092 и 0,144 кг. Таблица 2
Примечание. Номинальный диаметр арматурного каната соответствует диаметру окружности, описанной вокруг его сечения. ПРИЛОЖЕНИЕ 3ОСНОВНЫЕ БУКВЕННЫЕ ОБОЗНАЧЕНИЯУСИЛИЯ ОТ ВНЕШНИХ НАГРУЗОК И
ВОЗДЕЙСТВИЙ В ПОПЕРЕЧНОМ СЕЧЕНИИ ЭЛЕМЕНТА М - изгибающий момент или момент внешних сил
относительно центра тяжести приведенного сечения; N - продольная сила; Q - поперечная сила; Т - крутящий момент; Msh, Ml, Mtot - изгибающие моменты
соответственно от кратковременных нагрузок, от постоянных и длительных нагрузок
и от всех нагрузок, включая постоянные, длительные и кратковременные. ХАРАКТЕРИСТИКА
ПРЕДВАРИТЕЛЬНОГО НАПРЯЖЕННОГО ЭЛЕМЕНТА Р - усилие предварительного обжатия, определяемое по
формуле (8), с учетом потерь предварительного напряжения в арматуре,
соответствующих рассматриваемой стадии работы элемента; Р1, Р2
- то же, с учетом соответственно первых и всех потерь напряжений; ssp, s¢sp - предварительные
напряжения соответственно в напрягаемой арматуре S и S¢ до обжатия бетона (при
натяжении арматуры на упоры) или в момент снижения величины предварительного
напряжения в бетоне до нуля воздействием на элемент внешних фактических или
условных сил, определяемые, согласно указаниям пп. 1.15, 1.19 и 1.20, с учетом
потерь предварительного напряжения в арматуре, соответствующих рассматриваемой
стадии работы элемента; ssp1, ssp2 - напряжения ssp с учетом соответственно
первых и всех потерь; sbp - сжимающие напряжения в
бетоне в стадии предварительного обжатия, определяемые, согласно пп. 1.21 и
1.22, с учетом потерь предварительного напряжения в арматуре, соответствующих
рассматриваемой стадии работы элементов; gsp - коэффициент точности
натяжения арматуры, определяемый согласно указаниям п. 1.18. ХАРАКТЕРИСТИКИ
МАТЕРИАЛОВ Rb, Rb,ser - расчетные сопротивления бетона осевому сжатию для
предельных состояний соответственно первой и второй групп; Rbt, Rbt,ser - расчетные сопротивления бетона осевому растяжению
для предельных состояний соответственно первой и второй групп; Rbp - передаточная прочность
бетона, назначаемая согласно указаниям п. 2.3;
Rs, Rs,ser - расчетное сопротивление арматуры растяжению для
предельных состояний соответственно первой и второй групп; Rsw - расчетное сопротивление
поперечной арматуры растяжению, определяемое согласно указаниям п. 2.25; Rsc - расчетное сопротивление
арматуры сжатию для предельных состояний первой группы; Eb - начальный модуль
упругости бетона при сжатии и растяжении; Es - модуль упругости
арматуры; a - отношение соответствующих
модулей упругости арматуры Es и бетона Eb. ХАРАКТЕРИСТИКИ ПОЛОЖЕНИЯ
ПРОДОЛЬНОЙ АРМАТУРЫ В ПОПЕРЕЧНОМ СЕЧЕНИИ ЭЛЕМЕНТА S - обозначение продольной
арматуры: а) при наличии
сжатой и растянутой от действия внешней нагрузки зон сечения - расположенной в
растянутой зоне; б) при полностью
сжатом от действия внешней нагрузки сечении - расположенной у менее сжатой
грани сечения; в) при полностью
растянутом от действия внешней нагрузки сечении внецентренно растянутых
элементов - расположенной у более растянутой грани сечения; S¢ - обозначение продольной
арматуры: а) при наличии
сжатой и растянутой от действия внешней нагрузки зон сечения - расположенной в
сжатой зоне; б) при полностью
сжатом от действия внешней нагрузки сечении - расположенной у более сжатой грани
сечения; в) при полностью
растянутом от действия внешней нагрузки сечении внецентренно растянутых
элементов - расположенной у менее растянутой грани сечения. b - ширина прямоугольного
сечения; ширина ребра таврового и двутаврового сечений; bf, b¢f - ширина полки таврового и
двутаврового сечений соответственно в растянутой и сжатой зонах; h - высота прямоугольного,
таврового и двутаврового сечений; hf, h¢f - высота полки таврового и
двутаврового сечений соответственно в растянутой и сжатой зонах; D - диаметр кольцевого или
круглого сечения; Asp, A¢sp - площадь сечения
напрягаемой части арматуры соответственно S и S¢; As, A¢s - площадь сечения
ненапрягаемой части арматуры соответственно S и S¢; а - расстояние от равнодействующих усилий в арматуре S до ближайшей грани; а¢ - расстояние от
равнодействующих предельных растягивающих усилий в арматуре S¢ до ближайшей грани; а¢s, a¢p - расстояние от
равнодействующей усилий в арматуре соответственно площадью A¢s и A¢sp до ближайшей грани; h0 - рабочая высота сечения,
равная h - a; х - высота сжатой зоны бетона; x - относительная высота
сжатой зоны бетона, равная х/h0; s - расстояние между
хомутами, измеренное по длине элемента; е0 - эксцентриситет продольной силы N относительно центра тяжести
приведенного сечения, равный M/N и определяемый в
соответствии с указаниями п. 3.35; е0р - эксцентриситет усилия
предварительного обжатия Р
относительно центра тяжести приведенного сечения, определяемый в соответствии с
указаниями п. 1.19; е0,tot - эксцентриситет
равнодействующей продольной силы N и
усилия предварительного обжатия Р
относительно центра тяжести приведенного сечения; е, е¢ - расстояние от точки
приложения продольной силы N до
равнодействующей усилий в арматуре соответственно S и S¢; es, esp - расстояние соответственно
от точки приложения продольной силы N и
усилия предварительного обжатия Р до
центра тяжести сечения арматуры S; l - пролет элемента; l0 - расчетная длина элемента,
подвергающегося действию сжимающей силы; i - радиус инерции поперечного
сечения элемента относительно центра тяжести сечения; d - номинальный диаметр
стержней арматурной стали; Asw - площадь сечения хомутов,
расположенных в одной нормальной к продольной оси элемента плоскости,
пересекающей наклонное сечение; As,inc - площадь сечения отогнутых стержней, расположенных
в одной наклонной к продольной оси элемента плоскости, пересекающей наклонное
сечение; m - коэффициент армирования,
определяемый как отношение площади сечения арматуры S к площади поперечного элемента bh0 без учета свесов сжатых и растянутых полок; А - площадь всего бетона в поперечном сечении; Ared - площадь приведенного
сечения элемента, определяемая в соответствии с указаниями п. 1.21; I - момент инерции сечения
бетона относительно центра тяжести сечения элемента; Ired - момент инерции
приведенного сечения элемента относительно его центра тяжести, определяемый в
соответствии с указаниями п. 1.21. Однобуквенные индексы а - accidental (случайный); b - beton
(бетон, сжатый бетон); c - compressive (сжатие); e - eccentricity (эксцентриситет); f - flange
(полка балки); f - force (нагрузка); l - long
(длительный); l - left
(левый); m - middle
(средний); m - moment
(момент); m - main
(главный); n - normative (нормативный); n - normal
[продольная (нормальная) сила]; p - prestress (усилие обжатия, предварительное напряжение); R - расчетное сопротивление; r - right (правый); r - ядровая точка
(расположенная на расстоянии r от центра тяжести); s - steel
(сталь, арматура); t - tention
(растяжение); t - torsion
(кручение); u - ultimate (предельный); w - web (ребро или стенка балки). Двух- и трехбуквенные
индексы an - anchoring (анкеровка); cir - circular (кольцевой); cr - сritical
(критический); crc - cracking (трещинообразование, трещина); el - elastic (упругий); ext - extern
(внешний, наружный); inc - incline
(наклонный, отогнутый); inf - infereior (нижний); ov - overhang (свес полки); pl - plastic
(пластичный, неупругий); red - reduction (приведенный); ser - service
(эксплуатационный); sh - short
(кратковременный); sup - super (верхний); tot - total
(суммарный, полный). Примечание. Двух- и трехбуквенные индексы отделяются от других индексов запятой. Однобуквенные индексы запятой не отделяются. СОДЕРЖАНИЕ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
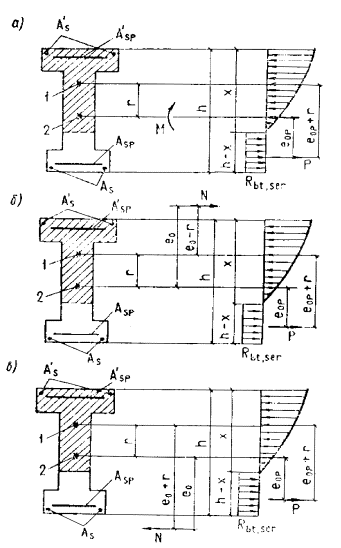
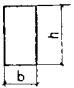
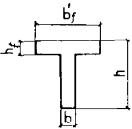
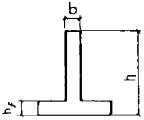
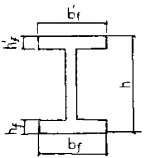
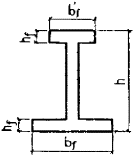
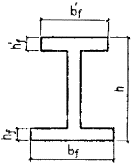
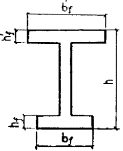
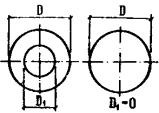
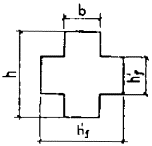
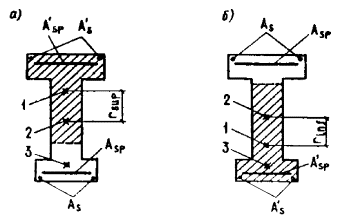
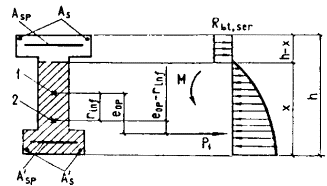
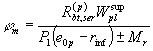 , но не менее 0,45,
, но не менее 0,45,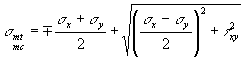 ,
,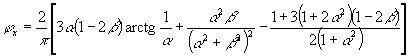 ;
;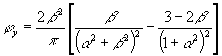 ;
;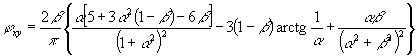 .
.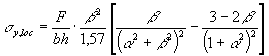 ,
,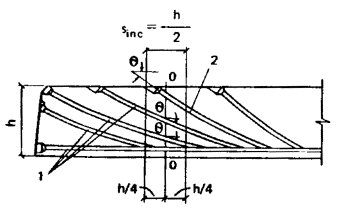
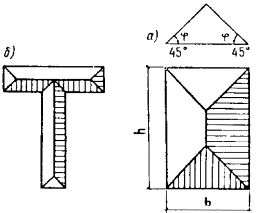
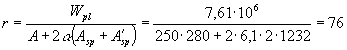
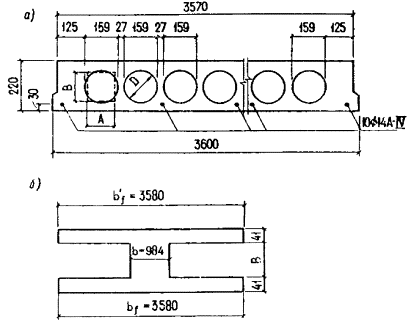
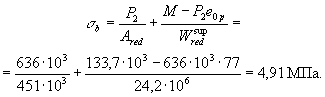
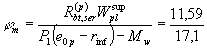
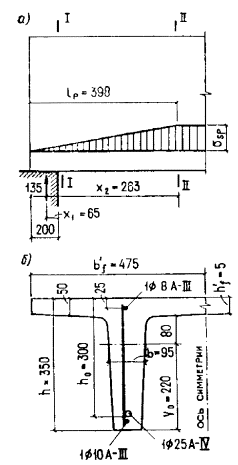
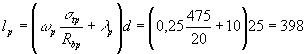
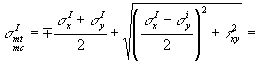
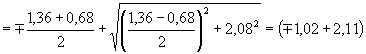
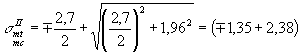
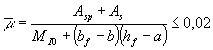
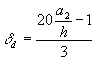
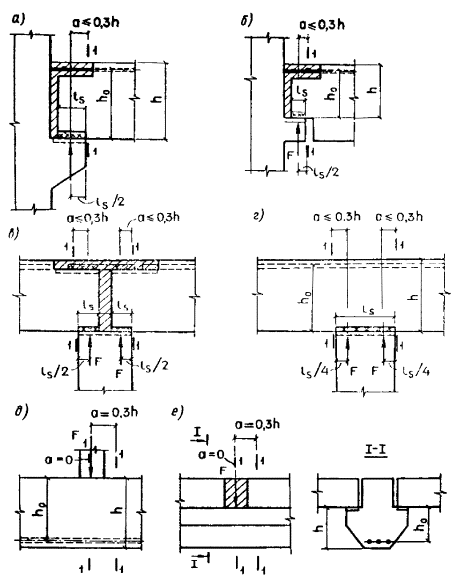
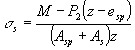 ;
;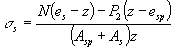 ;
;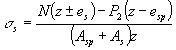 ;
;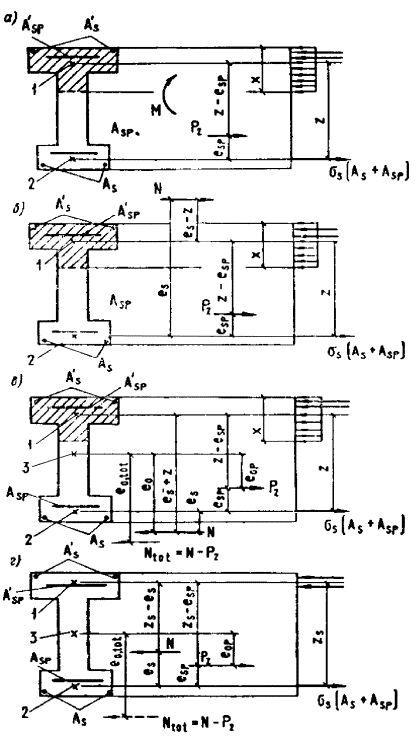
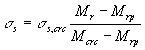 ,
,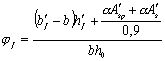 ;
; 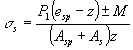
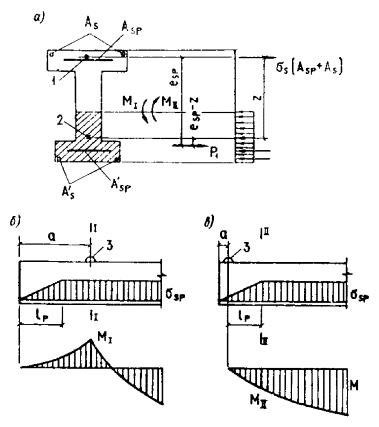
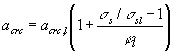 ,
,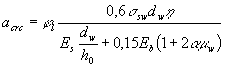 ,
,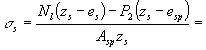
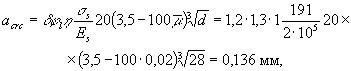
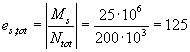
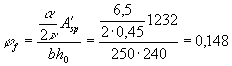 ;
;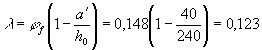 ;
;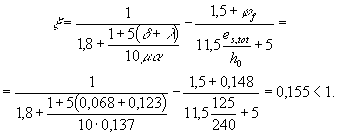
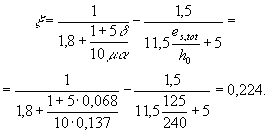
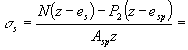
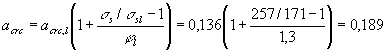
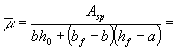
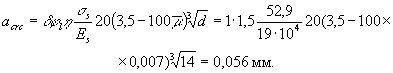
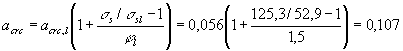
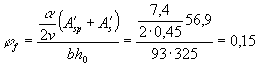 ;
;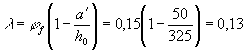
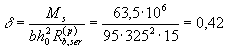 ;
;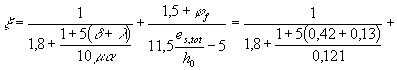
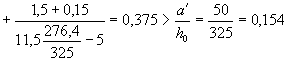 ;
;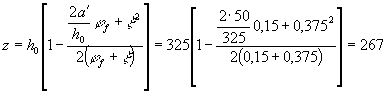
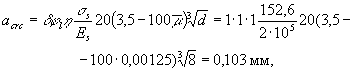
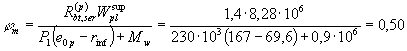 ,
,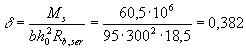 ;
;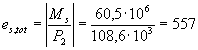
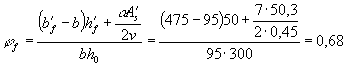 ;
;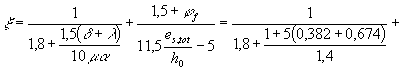
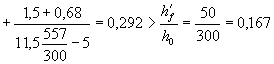 ;
;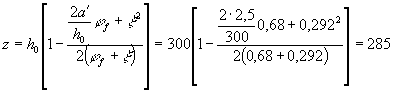
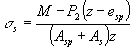 =
=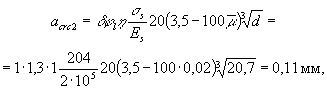
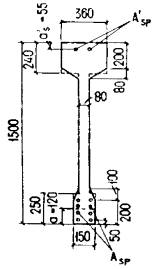
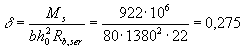 ;
;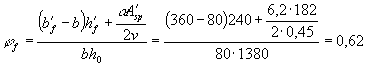 ;
;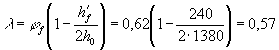 ;
; 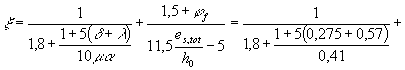
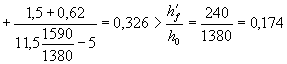 ;
;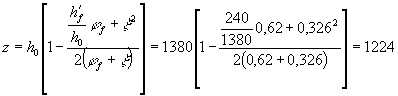
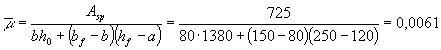 ;
;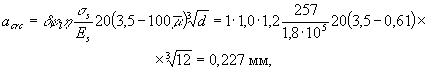
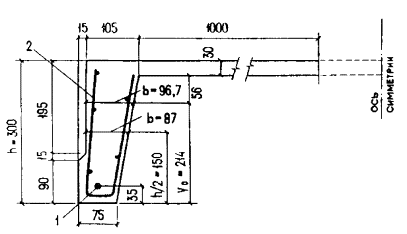
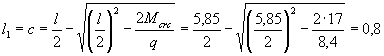
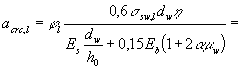
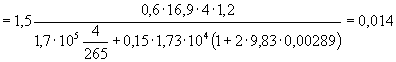
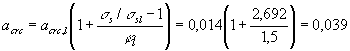
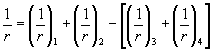 ,
,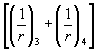
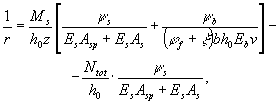
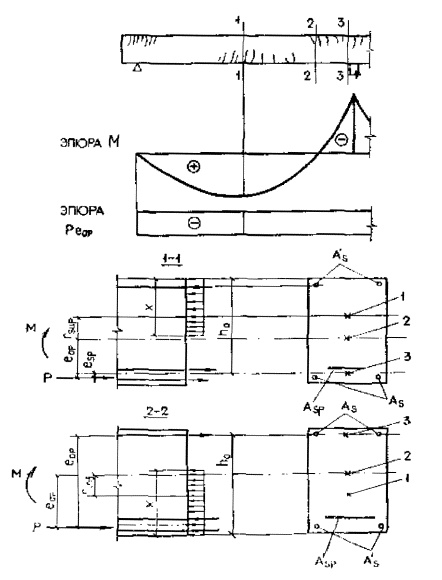
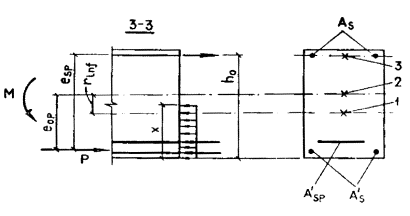
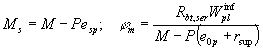 ;
;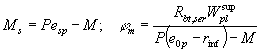 ;
;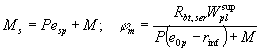 ;
;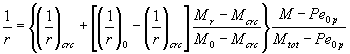
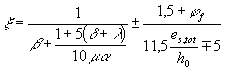 ,
,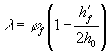 ;
;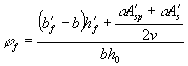 ;
;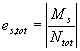 .
.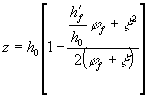 .
.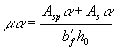 ;
; 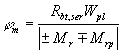 ,
,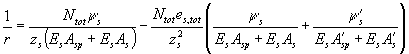 ,
,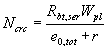 ;
; 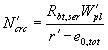
 .
.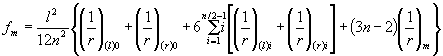 ,
,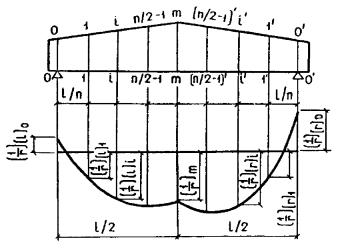
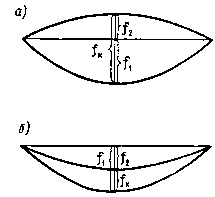
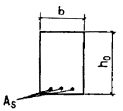
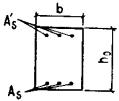
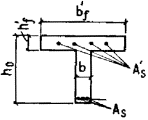
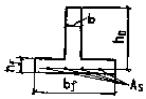
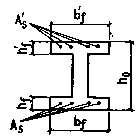
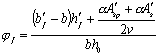 ;
; 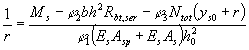 ,
,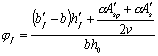 ;
; 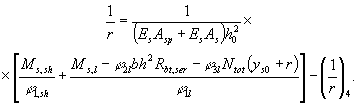
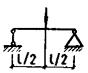
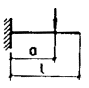
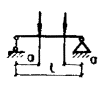
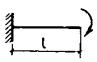
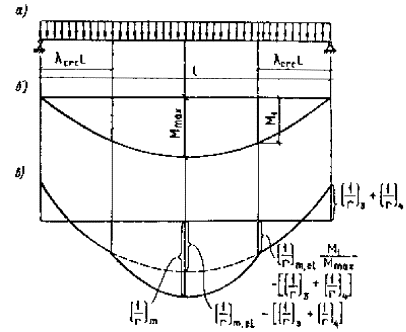
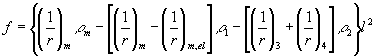 ,
,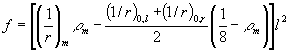 ,
,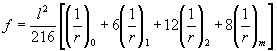 ,
,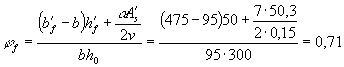
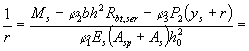
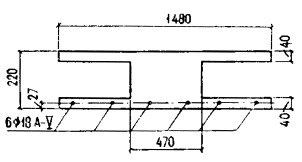
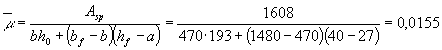
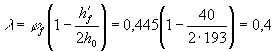 ;
;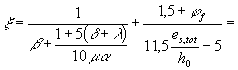
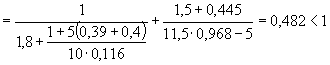 ;
;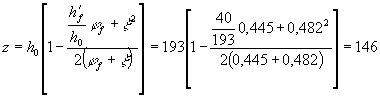
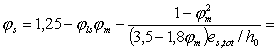
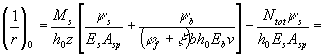
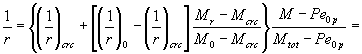
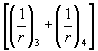
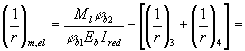

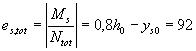
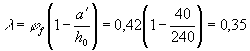 ;
;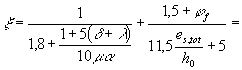
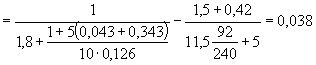 .
.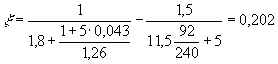 .
.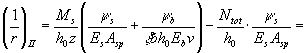

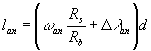
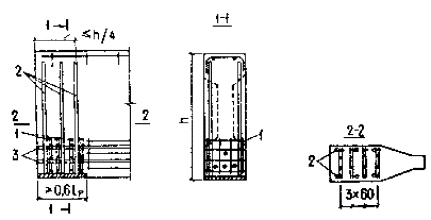
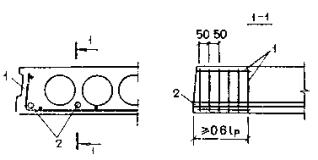
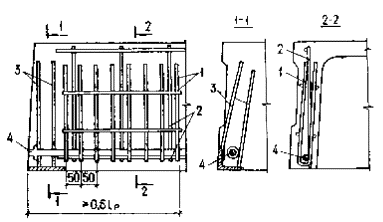
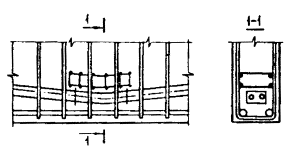
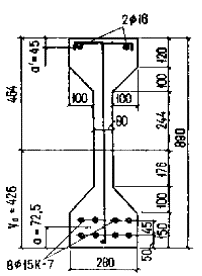
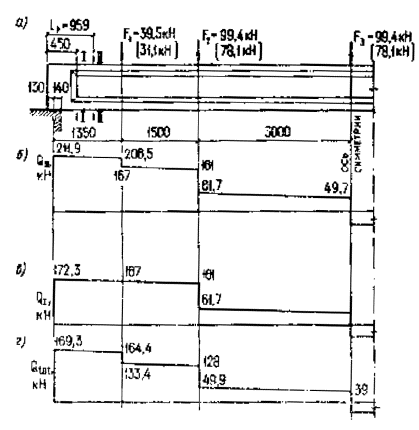
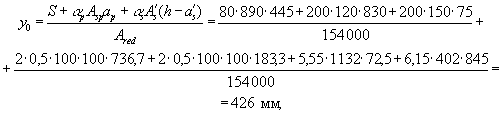
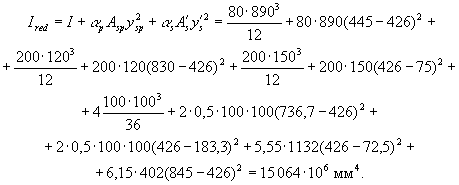
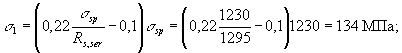
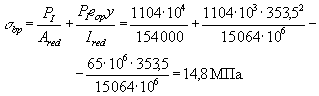
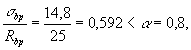
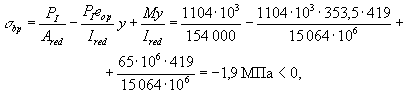
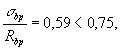
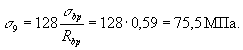 Таким образом, напряжение
Таким образом, напряжение 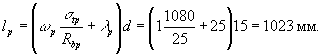
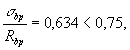
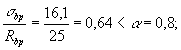
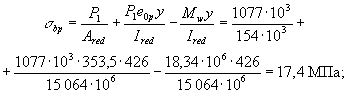
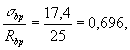
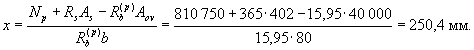
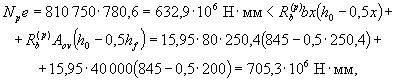
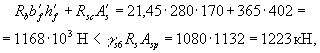
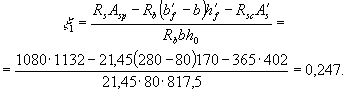
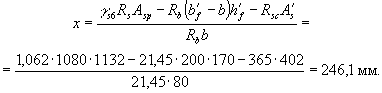
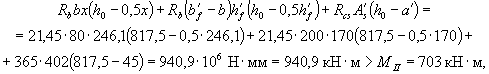
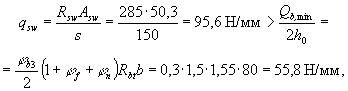
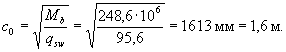
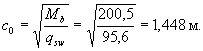
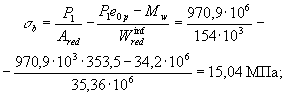
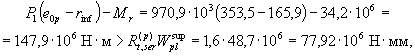
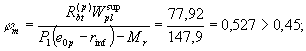
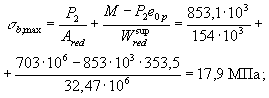
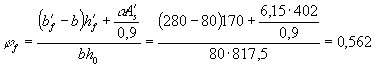 ;
;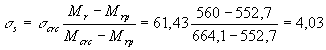
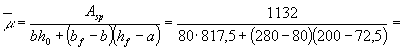
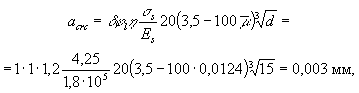
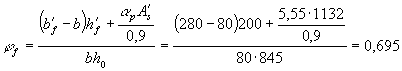
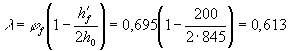
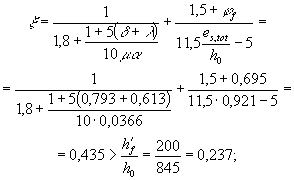
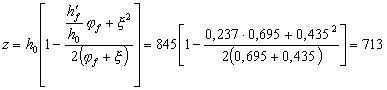
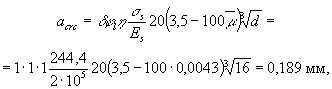
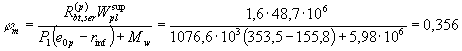 ;
;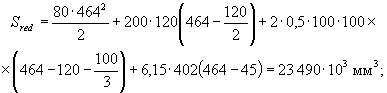
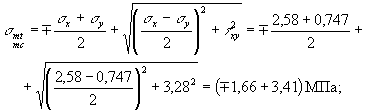
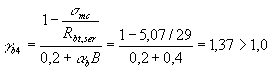 .
.