|
|
ГОСТ Р 50779.21-96 ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ОРГАНИЗАЦИИ СТАТИСТИЧЕСКИЕ МЕТОДЫ ПРАВИЛА ОПРЕДЕЛЕНИЯ
И МЕТОДЫ РАСЧЕТА СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК ПО ВЫБОРОЧНЫМ ДАННЫМ Часть 1. НОРМАЛЬНОЕ
РАСПРЕДЕЛЕНИЕ ГОССТАНДАРТ РОССИИ МОСКВА Предисловие 1 РАЗРАБОТАН И ВНЕСЕН
Техническим комитетом по стандартизации «Стандартизация статистических методов
управления качеством» ТК 125 АО «Нижегородский
научно-исследовательский центр контроля и диагностики технических систем» (АО
НИЦ КД) 2 ПРИНЯТ И ВВЕДЕН В ДЕЙСТВИЕ Постановлением
Госстандарта России от 14 августа 1996 г. № 513 3 В настоящем стандарте
учтены требования международного стандарта ИСО 2854-76 «Статистическое
представление данных. Методы оценки и проверки гипотез о средних значениях и
дисперсиях» 4 ВВЕДЕН ВПЕРВЫЕ СОДЕРЖАНИЕ 6 точечное
и интервальное оценивание математического ожидания генеральной совокупности 7 точечное
и интервальное оценивание дисперсии генеральной совокупности 8 точечное и интервальное оценивание доли распределения
случайной величины в заданном интервале Приложение а (справочное) Таблица значений функции стандартного нормального закона
распределения Приложение б (справочное) Таблица значений квантилей распределения стьюдента Приложение в (справочное) Таблица значений квантилей c2-распределения Приложение г (справочное) Таблицы значений квантилей распределения фишера Введение Стандарт устанавливает
процедуры и методы решения ряда практических задач статистики в случае, когда наблюдаемые
величины являются случайными и распределены по нормальному закону. В стандарте изложены методы
решения следующих задач: а) точечного оценивания
параметров нормального распределения случайной величины; б) точечного оценивания
вероятности попадания (доли распределения) случайной величины в заданный
интервал и вне его; в) интервального
(доверительного) оценивания параметров и величин, указанных в подпунктах а и б; г) проверки гипотез об этих
же величинах. Все приводимые процедуры
используют ограниченный ряд статистических независимых наблюдений, полученных в
производстве, в лабораторных условиях, при контроле, измерении, оценке и т. п. ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ Статистические
методы ПРАВИЛА
ОПРЕДЕЛЕНИЯ И МЕТОДЫ РАСЧЕТА СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК ПО ВЫБОРОЧНЫМ ДАННЫМ Часть 1.
Нормальное распределение Statistical methods.
Determination rules and methods for calculation of
statistical characteristics based on sample data. Part 1. Normal distribution Дата введения 1997-07-01 1 ОБЛАСТЬ ПРИМЕНЕНИЯСтандарт устанавливает
методы, применяемые для: - оценки математического
ожидания и дисперсии генеральной совокупности; - проверки гипотез
относительно значений этих параметров; - оценки вероятности
попадания (доли распределения) случайной величины в заданный интервал. Примечание - Вероятность попадания случайной величины в интервал равна доле распределения случайном величины в этом интервале. В большинстве практических задач физический смысл имеет понятие «доля распределения случайной величины в интервале», которое далее используют в данном стандарте. Методы, изложенные в
настоящем стандарте, применимы в том случае, если выполнены следующие условия: - элементы выборки получены
путем независимых повторений эксперимента. В случае конечной генеральной
совокупности объем должен составлять не более 10 % объема генеральной
совокупности; - наблюдаемые переменные
распределены по нормальному закону. Однако, если распределение вероятностей не
сильно отличается от нормального, то описанные в стандарте методы остаются
применимыми для большинства практических приложений. В этом случае объем
выборки должен быть не менее 10, причем достоверность получаемых статистических
выводов возрастает при увеличении объемов выборок. 2 НОРМАТИВНЫЕ ССЫЛКИВ настоящем стандарте
использована ссылка на ГОСТ
15895-77 Статистические методы управления качеством продукции. Термины и
определения 3 ОПРЕДЕЛЕНИЯВ настоящем стандарте
применяют термины по ГОСТ
15895, а также приведенные ниже: Точечное оценивание параметра - получение оценки параметра в виде одного
численного значения. Интервальное (доверительное) оценивание параметра - получение оценки
параметра в виде доверительного интервала. Доверительный интервал - интервал, границы которого являются функциями от
выборочных данных и который накрывает истинное значение оцениваемого параметра
с вероятностью не менее (1 - a), где (1 - a) - доверительная
вероятность. Примечание - Доверительный интервал может быть двусторонним или односторонним. Нулевая гипотеза - предположение о распределении генеральной совокупности, которое
проверяется по статистическим данным. В частности, в данном стандарте
рассматривают предположения о значениях параметров распределения. 4 ОБОЗНАЧЕНИЯ И СОКРАЩЕНИЯm - математическое ожидание
нормального закона распределения (среднее значение генеральной совокупности); Примечание - Далее по тексту - среднее значение. m0 - известное значение
параметра m; m1, m2 - математические ожидания
для двух различных генеральных совокупностей;
mв, mн - верхняя и нижняя
доверительные границы параметра m; (m1 - m2)Ù - точечная оценка разности значений параметров m1 и m2; s - стандартное (среднее
квадратическое) отклонение нормально распределенной случайной величины; D
- дисперсия
генеральной совокупности, D = s2; D0 - известное значение дисперсии
генеральной совокупности, D0
= s20; s0 - конкретное численное
значение параметра s; s01, s02 - известные значения
параметров s1 и s2 для двух генеральных совокупностей;
sв, sн - верхняя и нижняя
доверительные границы параметра s;
х - выборочное значение наблюдаемой случайной величины; х1 - выборочное значение
случайной величины из первой генеральной совокупности; х2 - то же, из второй
генеральной совокупности; n,
n1, n2 - объемы выборок;
S1, S2 - то же, для двух выборок
соответственно; a - риск первого рода
(вероятность отвергнуть гипотезу, когда она верна); (1 - a) - доверительная
вероятность, где a, 0 < a < 1, - уровень
значимости при проверке гипотез; v -
число степеней свободы; u1-a,
u1-a/2 - квантили стандартного
нормального закона распределения уровней 1 - a и 1 - a/2 соответственно; t1-a(v), t1-a/2(v) - квантили распределения
Стьюдента с v степенями свободы уровней 1-a и 1 - a/2 соответственно; F1-a(v1, v2) - квантиль распределения Фишера уровня 1 - a с v1 и v2
степенями свободы; c21-a(v), c21-a/2(v), c2a/2(v) - квантили c2-распределения c v степенями свободы уровней 1 - a, 1 - a/2 и a/2 соответственно; L,
М - нижняя и верхняя границы
заданного интервала; р - доля распределения (вероятность попадания) случайной величины в
заданном интервале [L,
М]; q
- доля
распределения (вероятность попадания) случайной величины вне интервала [L, М], причем q + р = 1;
pн, qн - нижние односторонние доверительные границы для р и q; pв, qв - верхние односторонние доверительные границы для р и q; С - случайное событие, например: попадание случайной величины в заданный
интервал; Prob {С} - вероятность случайного события С; Sх - сумма выборочных значений х. 5 ОБЩИЕ ТРЕБОВАНИЯ5.1 Настоящий стандарт
содержит описание типовых статистических задач и процедур, при помощи которых
они решаются. Представленные задачи могут быть разбиты на три класса: - точечное и интервальное
оценивание среднего значения генеральной совокупности; - точечное и интервальное
оценивание дисперсии генеральной совокупности; - точечное и интервальное
оценивание доли распределения (вероятности попадания) случайной величины в
заданном интервале и вне его. 5.2 Для решения каждой из
перечисленных задач по 5.1 приведены процедуры их решения (разделы 6, 7, 8), включающие в
себя: 1) исходные и статистические
данные; 2) определение стандартных
табличных данных, которые необходимы для проведения вычислений (приложения А, Б, В, Г), а также
проведения вычислений параметров и коэффициентов по приведенным формулам; 3) результаты, полученные в
итоге проведенных вычислений. 5.3 Для задач каждого класса
приведены примеры их применения на практике (в производстве, медицине, химии).
Спектр возможных применений этих задач не ограничивается приведенными в разделах 6, 7, 8 примерами. 5.4 Во всех приведенных
задачах предполагается, что исходные статистические данные подчиняются
нормальному закону распределения. В тех случаях, когда изначально в этом нет
достаточной уверенности, должны быть проведены предварительные исследования
соответствия исходных данных нормальному закону. 5.5 Процедуры решения
перечисленных в 5.2
задач представлены в таблицах, соответствующих этим задачам (разделы 6, 7, 8). Для удобства пользования
таблицами разделов 6,
7, 8 задачи
соответствующих разделов перечислены в обобщенных таблицах 5.1, 5.2, 5.3, 5.4. Таблица 5.1 - Номера таблиц для решения задач по оценке среднего значения (раздел 6)
Таблица 5.2 - Номера таблиц для решения задач по оценке
дисперсии (раздел 7)
Таблица 5.3 - Номера таблиц для решения задач по
точечной оценке доли распределения случайной величины в заданном интервале (раздел 8) Таблица
5.4 -
Номера таблиц для решения задач по интервальной оценке доли распределения
случайной величины при неизвестной дисперсии в заданном интервале
5.6 Процедуры интервального
оценивания доли распределения случайной величины в заданном интервале,
изложенные в разделе 8
настоящего стандарта, являются простыми для применения, но не самыми
эффективными. Более эффективными являются процедуры с использованием таблиц
нецентрального распределения Стьюдента или таблиц толерантных множителей,
которые не приводятся в настоящем стандарте. 6 ТОЧЕЧНОЕ И ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ6.1 Алгоритм точечного и
интервального оценивания среднего значения при известной дисперсии приведен в
таблице 6.1. Таблица
6.1 - Оценка среднего значения при известной дисперсии
Примеры 1 Определение настроенности
станка-автомата при механической обработке (например, токарного,
шлифовального). Точность станка, определяемая разбросом получаемых размеров
деталей без изменения настройки, считается известной, а центр настройки m требуется определить. Возможны
оценки в виде точечного значения - двусторонним, если
необходима уверенность с заданной доверительной вероятностью в каких пределах
может лежать m; - односторонним с верхней
границей, если необходима уверенность, что m не выше какого-то значения: - односторонним с нижней
границей, если необходима уверенность, что m не ниже какого-то значения. 2 Оценка настройки
автоматического оборудования для розлива жидкости в тару. Условие и возможные
типы оценок - как в примере
1. 3 Многие другие
технологические процессы с известной или оцененной заранее точностью (т. е.
известным параметром s20), в которых выходной
контролируемый параметр имеет равновозможные отклонения в большую и меньшую
стороны от центра настройки m. Условие и возможные типы
оценок - как в примере
1. 6.2 Алгоритм точечного и
интервального оценивания среднего значения при неизвестной дисперсии приведен в
таблице 6.2. Таблица
6.2 - Оценка среднего значения при неизвестной дисперсии
Пример - Примеры те же, что
и в 6.1, но
точность, определяемая разбросом контролируемых значений, заранее неизвестна. 6.3 Алгоритм решения задачи
сравнения неизвестного среднего значения с заданным значением m0 при известной дисперсии
приведен в таблице 6.3. Таблица
6.3 - Сравнение среднего значения с заданным значением m0 при известной дисперсии
Пример - Проверка правильности
настройки технологического процесса на середину поля допуска или на заданное
оптимальное значение. Точность технологического процесса предполагается
известной или заранее оцененной, т. е. значение s20 известно. Возможные технологические
процессы: механическая обработка, расфасовка и другие, где равновозможны
отклонения контролируемого параметра в большую и меньшую сторону от центра
настройки. 6.4 Алгоритм решения задачи
сравнения неизвестного среднего значения с заданным значением m0 при неизвестной дисперсии
приведен в таблице 6.4. Таблица
6.4 - Сравнение среднего значения с заданным значением m0 при неизвестной дисперсии
Примеры 1 То же, что и в примере 6.3,
но точность технологического процесса заранее неизвестна. 2 Контрольные проверки в
розничной торговле и сфере обслуживания. Например, у пяти человек,
купивших по 1 кг сливочного масла, проводят повторное взвешивание товара на
контрольных, более точных весах. При этом должен быть получен ответ на вопрос: являются ли отклонения от
точного веса случайными или имеется систематическое обвешивание покупателей. То же - при отпуске бензина
и масел на автозаправочных станциях, то же - при продаже тканей в магазинах и
т. п. 6.5 Алгоритм решения задачи
сравнения двух неизвестных средних значений при известных дисперсиях приведен в
таблице 6.5. Таблица
6.5 - Сравнение двух средних значений при известных дисперсиях
1 Технологический процесс
механической обработки проводят параллельно на двух станках, точность каждого
из них известна, т. е. известны параметры s01 и s02. Можно ли считать, что оба
станка настроены одинаково? Можно ли смешивать детали, произведенные на этих
двух станках? Это бывает существенно, если дальнейшие технологические процессы
подстраивают под среднее значение - параметр данного технологического процесса. 2 Требуется определить,
одинаково ли среднее значение - параметр содержание кофеина в двух партиях
таблеток аскофена, выпущенных разными фармацевтическими заводами. При этом
заранее известны характеристики разброса этого содержания (т. е. дисперсии) для
каждого из двух заводов. 6.6 Алгоритм решения задачи
сравнения двух средних значении при неизвестных, но равных дисперсиях приведен
в таблице 6.6. Таблица
6.6 - Сравнение двух средних значений при неизвестных дисперсиях
Примечание - Дисперсии неизвестны, но в предположении могут быть равными. Примеры 1 Примеры те же, что и для 6.5, но дисперсии неизвестны. Применение этих
задач может встречаться чаще, чем задач в 6.5,
т. к. в большинстве случаев в двух сравниваемых процессах или совокупностях
дисперсии неизвестны. 2 Пример 2 из 6.5 может быть
распространен на сравнение содержания различных химических веществ или примесей
в двух совокупностях. 6.7 Алгоритм точечного и
интервального оценивания разности двух средних при известных дисперсиях
приведен в таблице 6.7. Таблица
6.7 - Оценка разности двух средних значений при известных дисперсиях
Пример - Сопоставление однотипных
средних значений показателя качества для двух технологических процессов или
двух совокупностей изделий. Считается, что дисперсии для обоих технологических
процессов или совокупностей известны. Например, оценка разности
средней толщины гальванического покрытия двух партий одинаковых изделий; оценка
разности среднего содержания вредных примесей в двух партиях химикатов и т. п. 6.8 Алгоритм точечного и
интервального оценивания разности двух средних значений при неизвестных, но
равных дисперсиях приведен в таблице 6.8. Таблица
6.8 - Оценка разности двух средних
значений при неизвестных, но равных* дисперсиях ___________ * Гипотезы равенства дисперсий двух генеральных совокупностей могут быть проверены по таблице 7.3 раздела 7.
Пример - Пример тот же; что и в 6.7, но
дисперсии неизвестны. Применение этих оценок может встречаться чаще, чем оценки
в 6.7, т.
к. в большинстве случаев в двух сравниваемых совокупностях дисперсии
неизвестны. 7 ТОЧЕЧНОЕ И ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ ДИСПЕРСИИ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ7.1 Алгоритм точечного и
интервального оценивания дисперсии или стандартного отклонения приведен в
таблице 7.1. Таблица
7.1 - Точечная и интервальная оценки дисперсии или стандартного отклонения
Примеры 1 Оценка точности (т. е.
средней величины разброса) показателей качества на выходе технологического
процесса. 2 Оценка точности
поддержания заданного значения параметра в системах автоматического
регулирования (например, температуры в печи). Если необходимо знать просто
среднее значение показателя точности, то делается точечная оценка s2 или s, а если необходима
уверенность в том, что точность не хуже (разброс не выше) определенного
значения, то делается интервальная оценка s2 или s с верхней доверительной
границей. 7.2 Алгоритм решения задачи
сравнения дисперсии или стандартного отклонения с заданной величиной приведен в
таблице 7.2. Таблица
7.2 - Сравнений дисперсии или стандартного отклонения с заданной величиной
Примеры 1 Оценка точности одного
оборудования или технологического процесса в сравнении с известной точностью
(т. е. известным параметром s0) другого оборудования или
технологического процесса. 2 Сравнение степени
однородности одной совокупности изделий (т. е. величины разброса показателя
качества) с известной заранее степенью однородности, характеризуемой
стандартным отклонением s0. 7.3 Алгоритм решения задачи
сравнения дисперсий или стандартных отклонений двух генеральных совокупностей
приведен в таблице 7.3. Таблица
7.3 - Сравнение дисперсий или стандартных отклонений двух генеральных совокупностей
Примеры 1 Сравнение точности двух
станков-автоматов по результатам контроля геометрических размеров деталей. 2 Соотношение стабильности
двух технологий, например отечественного и зарубежного предприятий, на основе
сравнения результатов контроля двух выборок из двух соответствующих
совокупностей изделий. 8 ТОЧЕЧНОЕ И ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ ДОЛИ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ В ЗАДАННОМ ИНТЕРВАЛЕ*___________ * Доля распределения случайной величины в заданном. интервале равна вероятности попадания случайной величины в этот интервал. В большинстве практических задач физический смысл имеет понятие «доля распределения случайной величины в интервале», используемый в данном стандарте, хотя все приведенные статистические выводы справедливы и для «вероятности попадания случайной величины в интервал». (Измененная редакция, Изм. №
1). 8.1 Алгоритм вычисления доли
распределения случайной величины в заданном интервале [L, М] и
вне его при известных параметрах нормального распределения приведен в таблице
8.1. Таблица 8.1 - Вычисление
доли распределения случайной величины в заданном интервале [L, М]
и вне его при известных параметрах нормального распределения (вспомогательный
алгоритм)
Для решения данной задачи не
используют выборочные данные, а значения параметров m и s2 считают известными. Таблица 8.1
содержит вспомогательный алгоритм для решения задач 8.2-8.9. Пример - Оценка ожидаемого уровня
несоответствий показателя качества продукции (уровня несоответствий) при
настройке станка на середину поля допуска или номинальное значение и известной
точности s20. 8.2 Алгоритм точечного
оценивания доли распределения случайной величины в заданном интервале [L, М] и вне его при известном стандартном
отклонении или дисперсии приведен в таблице 8.2. Таблица 8.2 - Точечная оценка доли
распределения случайной величины в заданном интервале [L, М] и вне его при известном стандартном
отклонении или дисперсии
Пример - Оценка уровня
несоответствия показателя качества продукции, который следует ожидать при
работе станка или технологического процесса при установленном допуске и
неизвестном уровне настройки. При этом считают, что точность станка или
технологического процесса известна или достаточно точно оценена заранее. 8.3 Алгоритм точечного
оценивания доли распределения случайной величины в заданном интервале [L, М] и вне его при неизвестной дисперсии
приведен в таблице 8.3. Таблица 8.3 - Точечная оценка доли распределения случайной величины в заданном интервале [L, М] и вне его при неизвестной дисперсии
Пример тот же, что и в 8.2, но точность
станка или технологического процесса неизвестна. 8.4 Алгоритм интервального
оценивания доли распределения случайной величины с неизвестной дисперсией в
одностороннем интервале выше заданной нижней границы L приведен в таблице 8.4. Таким образом определяют верхнюю
доверительную границу qв для доли распределения вне
одностороннего интервала с нижней границей L, а также нижнюю доверительную
границу рн для доли
распределения случайной величины в указанном интервале. Примечание - Здесь и далее следует различать заданный изначально односторонний или двусторонний интервал (допуск) с известной границей (границами) для случайной величины Х и доверительный интервал для доли распределения случайной величины в этом допуске и вне его. Границы заданного интервала (допуска) L и М для случайной величины измеряются в тех же единицах физических величин, что и случайная величина, например: в миллиметрах, граммах и т. п. Границы получаемого доверительного интервала являются безразмерными, как и сама вероятность. Примеры 1 Определение уровня
несоответствий для показателя «толщина гальванопокрытия». Случай, когда
необходимо иметь определенную уверенность в том, что уровень несоответствий не
превышает установленного предельного процента. 2 Оценка доли годных и
несоответствующих деталей по показателю качества «твердость после термической
обработки». Требование (допуск) одностороннее: L = 45 ед. Роквелла. Оценка получается в виде верхней доверительной
границы qв на долю несоответствующей продукции с твердостью
ниже 45 ед. Кроме того, получается нижняя доверительная граница рн
на долю продукции, соответствующей требованию, т. е. на долю деталей с
твердостью не ниже 45 ед. Доверительные оценки рн и qв, в отличие от точечных,
имеют характеристики достоверности утверждений (с вероятностью 1 - a): истинная доля годной
продукции не менее рн; истинная доля
несоответствующей продукции не более qв. Таблица
8.4 - Определение верхней qв
и нижней рн доверительных
границ для доли распределения случайной величины в одностороннем интервале и вне его с
заданной нижней границей L
(дисперсия неизвестна)
8.5 Алгоритм интервального
оценивания доли распределения случайной величины с неизвестной дисперсией в
одностороннем интервале ниже заданной верхней границы М приведен в таблице 8.5. Таким образом определяют верхнюю
доверительную границу qв для доли распределения вне
одностороннего интервала с верхней границей М, а также нижнюю доверительную
границу рн для доли
распределения случайной величины в указанном интервале. Таблица
8.5 - Определение верхней qв
и нижней рн доверительных
границ для доли распределения случайной величины в одностороннем интервале и вне его с
заданной верхней границей М
(дисперсия неизвестна)
Пример - Определение уровня
несоответствий для показателя «процент примесей» в металлургии или в
фармакологии. Случай, когда необходимо иметь определенную уверенность в том,
что уровень несоответствий не превышает установленного предельного процента. 8.6 Алгоритм интервального
оценивания доли распределения случайной величины с неизвестной дисперсией в
заданном интервале [L,
М] приведен в таблице 8.6.
Таким образом определяют верхнюю доверительную границу qв для доли распределения вне интервала [L, М], а также нижнюю доверительную
границу pн для доли распределения случайной величины в
данном интервале. Таблица
8.6 - Определение верхней qв
и нижней pн доверительных границ для
доли распределения
случайной величины в заданном интервале [L,
М] и вне его (дисперсия неизвестна)
Пример из 8.2, но точность станка заранее неизвестна. Случай,
когда необходимо иметь определенную уверенность в том, что уровень
несоответствий не превышает установленного предельного значения. 8.7 Алгоритм интервального
оценивания доли распределения случайной величины с неизвестной дисперсией в
одностороннем интервале выше заданной нижней границы L приведен в таблице 8.7.
Таким образом определяют нижнюю доверительную границу qн для доли распределения вне одностороннего интервала
с нижней границей L, а также верхнюю доверительную
границу рв для доли
распределения случайной величины в указанном интервале. Таблица
8.7 - Определение нижней qн
и верхней рв,
доверительных границ для доли распределения случайной величины в
одностороннем интервале и вне его с заданной нижней границей L (дисперсия неизвестна)
Пример - Доказательство (с
заданной вероятностью) того, что уровень несоответствий по данному показателю
качества превышает установленное в нормативной документации предельное
значение. Случай предъявления рекламаций на серийную или массовую продукцию по
определенному показателю качества. 8.8 Алгоритм интервального
оценивания доли распределения случайной величины с неизвестной дисперсией в
одностороннем интервале ниже заданной верхней границы М приведен в таблице 8.8. Таким образом определяют нижнюю
доверительную границу qн для доли распределения вне
одностороннего интервала с верхней границей М, а также верхнюю доверительную
границу рв для доли
распределения случайной величины в указанном интервале. Таблица 8.8 - Определение нижней qн и верхней рв, доверительных границ для
доли распределения
случайной величины в одностороннем интервале и вне его с заданной верхней
границей М (дисперсия неизвестна)
8.9 Алгоритм интервального
оценивания доли распределения случайной величины с неизвестной дисперсией в
заданном интервале [L,
М] приведен в таблице 8.9.
Таким образом определяют нижнюю доверительную границу qн для доли распределения вне интервала [L, М], а также верхнюю доверительную
границу рв для доли
распределения случайной величины в данном интервале. Таблица
8.9 - Определение нижней qн
и верхней рв,
доверительных границ для доли распределения случайной величины в заданном
интервале [L,
М] и вне его (дисперсия
неизвестна)
ПРИЛОЖЕНИЕ А
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
z |
Ф(z) |
Ф(0,5 + z) |
Ф(1,0 + z) |
Ф(l,5 + z) |
Ф(2,0 + z) |
Ф(2,5 + z) |
Ф(3,0 + z) |
|
0,00 |
0,50000 |
0,69146 |
0,84134 |
0,93319 |
0,97725 |
0,99379 |
0,99865 |
|
0,01 |
0,50399 |
0,69497 |
0,84375 |
0,93448 |
0,97778 |
0,99396 |
0,99869 |
|
0,02 |
0,50798 |
0,69847 |
0,84614 |
0,93574 |
0,97831 |
0,99413 |
0,99874 |
|
0,03 |
0,51197 |
0,70194 |
0,84850 |
0,93699 |
0,97882 |
0,99430 |
0,99878 |
|
0,04 |
0,51595 |
0,70540 |
0,85083 |
0,93822 |
0,97932 |
0,99446 |
0,99882 |
|
0,05 |
0,51994 |
0,70884 |
0,85314 |
0,93943 |
0,97982 |
0,99461 |
0,99886 |
|
0,06 |
0,52392 |
0,71226 |
0,85543 |
0,94062 |
0,98030 |
0,99477 |
0,99889 |
|
0,07 |
0,52790 |
0,71566 |
0,85769 |
0,94179 |
0,98077 |
0,99492 |
0,99893 |
|
0,08 |
0,53188 |
0,71904 |
0,85993 |
0,94295 |
0,98124 |
0,99506 |
0,99896 |
|
0,09 |
0,53586 |
0,72240 |
0,86214 |
0,94408 |
0,98169 |
0,99520 |
0,99900 |
|
0,10 |
0,53983 |
0,72575 |
0,86433 |
0,94520 |
0,98214 |
0,99534 |
0,99903 |
|
0,11 |
0,54380 |
0,72907 |
0,86650 |
0,94630 |
0,98257 |
0,99547 |
0,99906 |
|
0,12 |
0,54776 |
0,73237 |
0,86864 |
0,94738 |
0,98300 |
0,99560 |
0,99910 |
|
0,13 |
0,55172 |
0,73565 |
0,87076 |
0,94845 |
0,98341 |
0,99573 |
0,99913 |
|
0,14 |
0,55567 |
0,73891 |
0,87286 |
0,94950 |
0,98382 |
0,99585 |
0,99916 |
|
0,15 |
0,55962 |
0,74215 |
0,87493 |
0,95053 |
0,98422 |
0,99598 |
0,99918 |
|
0,16 |
0,56356 |
0,74537 |
0,87698 |
0,95154 |
0,98461 |
0,99609 |
0,99921 |
|
0,17 |
0,56750 |
0,74857 |
0,87900 |
0,95254 |
0,98500 |
0,99621 |
0,99924 |
|
0,18 |
0,57142 |
0,75175 |
0,88100 |
0,95352 |
0,98537 |
0,99632 |
0,99926 |
|
0,19 |
0,57535 |
0,75490 |
0,88298 |
0,95449 |
0,98574 |
0,99643 |
0,99929 |
|
0,20 |
0,57926 |
0,75804 |
0,88493 |
0,95543 |
0,98610 |
0,99653 |
0,99931 |
|
0,21 |
0,58317 |
0,76115 |
0,88686 |
0,95637 |
0,98645 |
0,99664 |
0,99934 |
|
0,22 |
0,58706 |
0,76424 |
0,88877 |
0,95728 |
0,98679 |
0,99674 |
0,99936 |
|
0,23 |
0,59095 |
0,76731 |
0,89065 |
0,95818 |
0,98713 |
0,99683 |
0,99938 |
|
0,24 |
0,59483 |
0,77035 |
0,89251 |
0,95907 |
0,98745 |
0,99693 |
0,99940 |
|
0,25 |
0,59871 |
0,77337 |
0,89435 |
0,95994 |
0,98778 |
0,99702 |
0,99942 |
|
0,26 |
0,60257 |
0,77637 |
0,89617 |
0,96080 |
0,98809 |
0,99711 |
0,99944 |
|
0,27 |
0,60642 |
0,77935 |
0,89796 |
0,96164 |
0,98840 |
0,99720 |
0,99946 |
|
0,28 |
0,61026 |
0,78230 |
0,89973 |
0,96246 |
0,98870 |
0,99728 |
0,99948 |
|
0,29 |
0,61409 |
0,78524 |
0,90147 |
0,96327 |
0,98899 |
0,99736 |
0,99950 |
|
0,30 |
0,61791 |
0,78814 |
0,90320 |
0,96407 |
0,98928 |
0,99744 |
0,99952 |
|
0,31 |
0,62172 |
0,79103 |
0,90490 |
0,96485 |
0,98956 |
0,99752 |
0,99953 |
|
0,32 |
0,62552 |
0,79389 |
0,90658 |
0,96562 |
0,98983 |
0,99760 |
0,99955 |
|
0,33 |
0,62930 |
0,79673 |
0,90824 |
0,96638 |
0,99010 |
0,99767 |
0,99957 |
|
0,34 |
0,63307 |
0,79955 |
0,90988 |
0,96712 |
0,99036 |
0,99774 |
0,99958 |
|
0,35 |
0,63683 |
0,80234 |
0,91149 |
0,96784 |
0,99061 |
0,99781 |
0,99960 |
|
0,36 |
0,64058 |
0,80511 |
0,91308 |
0,96856 |
0,99086 |
0,99788 |
0,99961 |
|
0,37 |
0,64431 |
0,80785 |
0,91466 |
0,96926 |
0,99111 |
0,99795 |
0,99962 |
|
0,38 |
0,64803 |
0,81057 |
0,91621 |
0,96995 |
0,99134 |
0,99801 |
0,99964 |
|
0,39 |
0,65173 |
0,81327 |
0,91774 |
0,97062 |
0,99158 |
0,99807 |
0,99965 |
|
0,40 |
0,65542 |
0,81594 |
0,91924 |
0,97128 |
0,99180 |
0,99813 |
0,99966 |
|
0,41 |
0,65910 |
0,81859 |
0,92073 |
0,97193 |
0,99202 |
0,99819 |
0,99968 |
|
0,42 |
0,66276 |
0,82121 |
0,92220 |
0,97257 |
0,99224 |
0,99825 |
0,99969 |
|
0,43 |
0,66640 |
0,82381 |
0,92364 |
0,97320 |
0,99245 |
0,99831 |
0,99970 |
|
0,44 |
0,67003 |
0,82639 |
0,92507 |
0,97381 |
0,99266 |
0,99836 |
0,99971 |
|
0,45 |
0,67364 |
0,82894 |
0,92647 |
0,97441 |
0,99286 |
0,99841 |
0,99972 |
|
0,46 |
0,67724 |
0,83147 |
0,92785 |
0,97500 |
0,99305 |
0,99846 |
0,99973 |
|
0,47 |
0,68082 |
0,83398 |
0,92922 |
0,97558 |
0,99324 |
0,99851 |
0,99974 |
|
0,48 |
0,68439 |
0,83646 |
0,93056 |
0,97615 |
0,99343 |
0,99856 |
0,99975 |
|
0,49 |
0,68793 |
0,83891 |
0,93189 |
0,97670 |
0,99361 |
0,99861 |
0,99976 |
|
Примечание - z - значение аргумента и от 0,00 до 0,49. Значение аргумента и от 0,50 и выше находят как сумму z и величин 0,5; 1,0; 1,5 и т. д. (см. заголовки колонок таблицы) |
|||||||
ПРИЛОЖЕНИЕ Б
(справочное)
ТАБЛИЦА ЗНАЧЕНИЙ КВАНТИЛЕЙ РАСПРЕДЕЛЕНИЯ СТЬЮДЕНТА
Б.1 В таблице Б.1
приведены значения квантилей ta(v) распределения Стьюдента
уровня a с v
степенями свободы.
Пример - Для v = 9
квантиль уровня a = 0,99 имеет значение
2,821.
Б.2 Квантили уровня a = 0,5 при любом v
имеют значение t = 0.
Б.3 Квантили уровня a < 0,5 находятся по
формуле
ta(v) = -ta-1(v).
(Измененная редакция, Изм. №
1).
Б.4 Для промежуточных
значений а, лежащих между двумя соседними табличными значениями a1 и a2:
a1 < a < a2,
значение квантиля ta(v) может быть вычислено
приближенно по формуле (метод линейной интерполяции):
 .
.
(Измененная редакция, Изм. №
1).
Пример - Для v = 9
требуется найти квантиль уровня a = 0,992. Полагаем: a1 = 0,99, a2 = 0,995; находим по таблице
t0,99 = 2,821, t0,995
= 3,250 и
вычисляем:
![]() ,
,
(Измененная редакция, Изм. №
1).
для v = 9 степеней свободы.
Таблица Б.1 - Значения квантилей распределения Стьюдента
|
v |
Значения квантилей распределения Стьюдента при уровне доверия а |
||||||||||||
|
0,55 |
0,6 |
0,65 |
0,7 |
0,75 |
0,8 |
0,85 |
0,9 |
0,95 |
0,975 |
0,99 |
0,995 |
0,9995 |
|
|
1 |
0,158 |
0,325 |
0,510 |
0,727 |
1,000 |
1,376 |
1,963 |
3,078 |
6,314 |
12,706 |
31,821 |
63,657 |
636,619 |
|
2 |
0,142 |
0,289 |
0,445 |
0,617 |
0,816 |
1,061 |
1,386 |
1,886 |
2,920 |
4,303 |
6,965 |
9,925 |
31,598 |
|
3 |
0,137 |
0,277 |
0,424 |
0,584 |
0,765 |
0,978 |
1,250 |
1,638 |
2,353 |
3,182 |
4,541 |
5,841 |
12,924 |
|
4 |
0,134 |
0,271 |
0,414 |
0,569 |
0,741 |
0,941 |
1,190 |
1,533 |
2,132 |
2,776 |
3,747 |
4,604 |
8,610 |
|
5 |
0,132 |
0,267 |
0,408 |
0,559 |
0,727 |
0,920 |
1,156 |
1,476 |
2,015 |
2.571 |
3.365 |
4,032 |
6,869 |
|
6 |
0,131 |
0,265 |
0,404 |
0,543 |
0,718 |
0,906 |
1,134 |
1,440 |
1,943 |
2,447 |
3,143 |
3,707 |
5,959 |
|
7 |
0,130 |
0,263 |
0,402 |
0,549 |
0,711 |
0,896 |
1,119 |
1,415 |
1,895 |
2,365 |
2,998 |
3,499 |
5.408 |
|
S |
0,130 |
0,262 |
0,399 |
0,546 |
0,706 |
0,889 |
1,108 |
1,397 |
1,860 |
2,306 |
2,896 |
3,355 |
5,041 |
|
9 |
0,129 |
0,261 |
0,398 |
0,543 |
0,703 |
0,883 |
1,100 |
1,383 |
1,833 |
2,262 |
2,821 |
3,250 |
4,781 |
|
10 |
0,129 |
0,260 |
0,397 |
0,542 |
0,700 |
0,879 |
1,093 |
1,372 |
1,812 |
2,228 |
2,764 |
3,169 |
4,587 |
|
11 |
0,129 |
0,260 |
0,396 |
0,540 |
0,697 |
0,876 |
1,088 |
1,363 |
1.796 |
2,201 |
2.718 |
3,106 |
4,437 |
|
12 |
0,128 |
0,259 |
0,395 |
0,539 |
0,695 |
0,873 |
1,083 |
1,356 |
1,782 |
2,179 |
2,681 |
3,055 |
4,318 |
|
13 |
0,128 |
0,259 |
0,394 |
0,538 |
0,694 |
0,870 |
1,079 |
1,350 |
1,771 |
2,160 |
2,650 |
3,012 |
4,221 |
|
14 |
0,128 |
0,258 |
0,393 |
0,537 |
0,692 |
0,868 |
1,076 |
1,345 |
1,761 |
2,145 |
2,624 |
2,977 |
4,140 |
|
13 |
0,128 |
0,258 |
0,393 |
0,536 |
0,691 |
0,866 |
1,074 |
1,341 |
1,753 |
2,131 |
2,602 |
2,947 |
4,173 |
|
16 |
0,128 |
0,258 |
0,392 |
0,535 |
0,690 |
0,865 |
1,071 |
1,337 |
1,746 |
2,120 |
2,583 |
2,921 |
4,015 |
|
17 |
0,128 |
0,257 |
0,392 |
0,534 |
0,689 |
0,863 |
1,069 |
1,333 |
1,740 |
2,110 |
2,567 |
2,898 |
3,965 |
|
18 |
0,127 |
0,257 |
0,392 |
0,534 |
0,688 |
0,862 |
1,067 |
1,330 |
1,734 |
2,101 |
2,552 |
2,878 |
3,922 |
|
19 |
0,127 |
0257 |
0,391 |
0,533 |
0,688 |
0,861 |
1,066 |
1,328 |
1,729 |
2,093 |
2,539 |
2,861 |
3,883 |
|
20 |
0,127 |
0,2a7 |
0,391 |
0,533 |
0,687 |
0,860 |
1,064 |
1,325 |
1,725 |
2,086 |
2,528 |
2,845 |
3,850 |
|
21 |
0,127 |
0,257 |
0,391 |
0,532 |
0,686 |
0,859 |
1,063 |
1,323 |
1,721 |
2,080 |
2,518 |
2,831 |
3,819 |
|
22 |
0,127 |
0,256 |
0,390 |
0,532 |
0,686 |
0,858 |
1,061 |
1,321 |
1,717 |
2,074 |
2,508 |
2,819 |
3,792 |
|
23 |
0,127 |
0,256 |
0,390 |
0,532 |
0,685 |
0,858 |
1,060 |
1,319 |
1,714 |
2,069 |
2,500 |
2,807 |
3,767 |
|
24 |
0,127 |
0,256 |
0,390 |
0,531 |
0,685 |
0,857 |
1,059 |
1,318 |
1,711 |
2,064 |
2,492 |
2,797 |
3,745 |
|
25 |
0,127 |
0,256 |
0,390 |
0,531 |
0,684 |
0,856 |
1,058 |
1,316 |
1,708 |
2,060 |
2,485 |
2,787 |
3,725 |
|
26 |
0,127 |
0,256 |
0,390 |
0,531 |
0,684 |
0,856 |
1,058 |
1,315 |
1,706 |
2.056 |
2,479 |
2,779 |
3,707 |
|
27 |
0,127 |
0,256 |
0,389 |
0,531 |
0,684 |
0,855 |
1,057 |
1,314 |
1,703 |
2,052 |
2,473 |
2,771 |
3,690 |
|
28 |
0,127 |
0,256 |
0,339 |
0,530 |
0,683 |
0,855 |
1,056 |
1,313 |
1,701 |
2,048 |
2,467 |
2,763 |
3,674 |
|
29 |
0,127 |
0,256 |
0,389 |
0,530 |
0,683 |
0,854 |
1,055 |
1,311 |
1,699 |
2,045 |
2,462 |
2,756 |
3,659 |
|
30 |
0,127 |
0,256 |
0,389 |
0,530 |
0,683 |
0,854 |
1,055 |
1,310 |
1,697 |
2,042 |
2,457 |
2,750 |
3,646 |
|
40 |
0,126 |
0,255 |
0,388 |
0,529 |
0,681 |
0,851 |
0,050 |
1,303 |
1,684 |
2,021 |
2,423 |
2,704 |
3,551 |
|
60 |
0,126 |
0,254 |
0,387 |
0,527 |
0,679 |
0,848 |
0,046 |
1,296 |
1,671 |
2,000 |
2,390 |
2,660 |
3,460 |
|
120 |
0,126 |
0,254 |
0,386 |
0,526 |
0,677 |
0,845 |
0,041 |
1,289 |
1,658 |
1,980 |
2.358 |
2,617 |
3,373 |
|
¥ |
0,126 |
0,253 |
0,385 |
0,524 |
0,674 |
0,842 |
0,036 |
1,282 |
1,645 |
1,960 |
2,326 |
2,576 |
3,291 |
ПРИЛОЖЕНИЕ В
(справочное)
ТАБЛИЦА ЗНАЧЕНИЙ КВАНТИЛЕЙ c2-РАСПРЕДЕЛЕНИЯ
B.1 В таблице B.1 приведены значения
квантилей c2a (v),
т. е. квантилей c2-распределения уровня a с v
степенями свободы.
Пример - Для v = 9 и a = 0,98 квантиль c20,98 = 19,679.
В.2 Для промежуточных
значений a, лежащих между двумя
соседними табличными значениями a1 и a2:
a1 < a < a2,
значение квантиля c2a может быть вычислено
приближенно по формуле (метод линейной интерполяции):
 .
.
(Измененная редакция, Изм. №
1).
Пример - Для v = 14
требуется найти квантиль уровня 0,988. Полагаем: a1 = 0,98; a2 = 0,99, находим по таблице B.1 c20,98 = 26,873; c20,99 = 29,141 и вычисляем:
![]()
для v = 14 степеней свободы.
Таблица
В.1 - Значения квантилей c2-распределения
|
v |
Значения квантилей c2-распределения при уровне доверия a |
||||||||||||
|
0,01 |
0,02 |
0,05 |
0,1 |
0,2 |
0,3 |
0,5 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
|
|
1 |
0,0157 |
0,0628 |
0,0393 |
0,0158 |
0,0642 |
0,148 |
0,455 |
1,074 |
1,642 |
2,706 |
3,841 |
5,412 |
6,635 |
|
2 |
0,0201 |
0,0404 |
0,103 |
0,211 |
0,446 |
0,713 |
1,386 |
2,408 |
3,219 |
4,605 |
5,991 |
7,824 |
9,210 |
|
3 |
0,115 |
0,185 |
0,352 |
0,584 |
1,005 |
1,424 |
2,366 |
3,665 |
4,642 |
6,251 |
7,815 |
9,837 |
11,345 |
|
4 |
0,297 |
0,429 |
0,711 |
1,064 |
1,649 |
2,195 |
3,357 |
4,878 |
5,989 |
7,779 |
9,488 |
11,668 |
13,277 |
|
5 |
0,554 |
0,752 |
1,145 |
1,160 |
2,343 |
3,000 |
4,351 |
6,064 |
7,289 |
9,233 |
11,070 |
13,388 |
15,086 |
|
6 |
0,872 |
1,134 |
1,635 |
2,204 |
3,070 |
3,828 |
5,348 |
7,231 |
8,558 |
10,645 |
12,592 |
15,033 |
16,812 |
|
7 |
1,239 |
1,564 |
2,167 |
2,833 |
3,822 |
4,671 |
6,346 |
8,383 |
9,803 |
12,017 |
14,067 |
16,622 |
18,475 |
|
8 |
1,646 |
2,032 |
2,733 |
3,490 |
4,594 |
5,527 |
7,344 |
9,524 |
11,030 |
13,362 |
15,507 |
18,168 |
20,090 |
|
9 |
2,088 |
2,532 |
3,325 |
4,168 |
5,380 |
6,393 |
8,343 |
10,656 |
12,242 |
14,684 |
16,919 |
19,679 |
21,666 |
|
10 |
2,358 |
3,059 |
3,940 |
4,865 |
6,179 |
7,267 |
9,342 |
11,781 |
13,442 |
15,987 |
18,307 |
21,161 |
23,209 |
|
11 |
3,053 |
3,609 |
4,575 |
5,578 |
6,989 |
8,148 |
10,341 |
12,899 |
14,631 |
17,275 |
19,675 |
22,618 |
24,725 |
|
12 |
3,571 |
4,178 |
5,226 |
6,304 |
7,807 |
9,034 |
11,340 |
14,011 |
15,821 |
18,549 |
21,026 |
24,054 |
26,217 |
|
13 |
4,107 |
4,765 |
5,892 |
7,042 |
8,634 |
9,926 |
12,340 |
15,119 |
16,985 |
19,812 |
22,362 |
25,472 |
27,688 |
|
14 |
4,660 |
5,368 |
6,571 |
7,790 |
9,467 |
10,821 |
13,339 |
16,222 |
18,151 |
21,064 |
23,585 |
26,873 |
29,141 |
|
15 |
5,229 |
5,985 |
7,261 |
8,547 |
10,307 |
11,721 |
14,339 |
17,322 |
19,311 |
22,307 |
24,996 |
28,259 |
30,578 |
|
16 |
5,812 |
6,614 |
7,962 |
9,312 |
11,152 |
12,624 |
15,333 |
18,418 |
20,465 |
23,542 |
26,296 |
29,633 |
32,000 |
|
17 |
6,408 |
7,255 |
8,672 |
10,035 |
12,002 |
13,531 |
16,338 |
19,511 |
21,615 |
24,769 |
27,587 |
30,995 |
33,409 |
|
18 |
7,015 |
7,906 |
9,390 |
10,865 |
12,857 |
14,440 |
17,338 |
20,601 |
22,760 |
25,989 |
28,869 |
32,346 |
34,805 |
|
19 |
7,633 |
8,567 |
10,117 |
11,651 |
13,716 |
15,352 |
18,338 |
21,689 |
23,900 |
27,204 |
30,144 |
33,687 |
36,191 |
|
20 |
8,260 |
9,237 |
10,851 |
12,443 |
14,578 |
16,266 |
19,337 |
22,775 |
25,038 |
28,412 |
31,410 |
35,020 |
37,566 |
|
21 |
8,897 |
9,915 |
11,591 |
13,240 |
15,445 |
17,182 |
20,337 |
23,858 |
26,171 |
29,615 |
32,671 |
36,343 |
38,932 |
|
22 |
9,542 |
10,600 |
12,338 |
14,041 |
16,314 |
18,101 |
21,337 |
24,939 |
27,301 |
30,813 |
33,924 |
37,659 |
40,289 |
|
23 |
10,196 |
11,293 |
13,091 |
14,848 |
17,187 |
19,021 |
22,337 |
26,018 |
28,429 |
32,007 |
35,172 |
38,968 |
41,638 |
|
24 |
10,856 |
11,992 |
13,848 |
15,659 |
18,062 |
19,943 |
23,337 |
27,096 |
29,553 |
33,196 |
36,415 |
40,270 |
42,980 |
|
25 |
11,524 |
12,697 |
14,611 |
16,473 |
18,940 |
20,867 |
24,337 |
28,172 |
30,675 |
34,382 |
37,652 |
41,566 |
44,314 |
|
26 |
12,198 |
13,409 |
15,379 |
17,292 |
19,820 |
21,792 |
25,336 |
29,246 |
31,795 |
35,563 |
38,885 |
42,856 |
45,642 |
|
27 |
12,879 |
14,125 |
16,151 |
18,114 |
20,703 |
22,719 |
26,336 |
30,319 |
32,912 |
36,741 |
40,113 |
44,140 |
46,963 |
|
28 |
13,565 |
14,847 |
16,928 |
18,939 |
21,588 |
23,647 |
27,336 |
31,391 |
34,027 |
37,916 |
41,337 |
45,419 |
48,278 |
|
29 |
14,256 |
15,574 |
17,708 |
19,768 |
22,475 |
24,577 |
28,336 |
32,461 |
35,139 |
39,087 |
42,557 |
46,693 |
49,588 |
|
30 |
14,953 |
16,306 |
18,493 |
20,599 |
23,364 |
25,508 |
29,336 |
33,530 |
36,250 |
40,256 |
43,773 |
47,962 |
50,892 |
ПРИЛОЖЕНИЕ Г
(справочное)
ТАБЛИЦЫ ЗНАЧЕНИЙ КВАНТИЛЕЙ РАСПРЕДЕЛЕНИЯ ФИШЕРА
Г.1 В таблицах Г.1-Г.9 содержатся
значения квантилей Fa
(v1, v2)
заданных уровней a для различных сочетаний
степеней свободы v1 и v2. Каждая таблица
соответствует одному уровню a, значение которого указано
в заголовке таблицы, и различным значениям v1 и v2.
Г.1.1 Для определения
квантилей уровней a меньше 0,5 следует
использовать соотношение:
![]() .
.
Г.1.2 Для промежуточных
значений a, лежащих между двумя
соседними значениями a1 и a2:
a1
< a < a2,
значение квантиля Fa может быть вычислено
приближенно по формуле
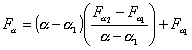 .
.
Г.1.3 Для промежуточных
значений v1 и v2, лежащих между двумя
соседними табличными значениями v¢1 и v1 или v¢2 и v2, т.
е.
v¢1 < v
< v1 или v¢2 < v < v2,
значения квантилей Fa(v1), Fa(v2) могут быть приближенно
вычислены по формулам
![]() ;
;
![]() .
.
(Измененная редакция, Изм. №
1).
ТАБЛИЦА Г.1 - КВАНТИЛИ F-РАСПРЕДЕЛЕНИЯ УРОВНЯ a = 0,5
|
v2 |
Квантили F-распределения уровня a = 0,5 для степеней свободы v1 |
||||||||||||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
12 |
15 |
20 |
24 |
30 |
40 |
60 |
120 |
¥ |
|
1 |
1,0000 |
1,5000 |
1,7092 |
1,8227 |
1,8937 |
1,9422 |
1,9774 |
2,0041 |
2,0250 |
2,0419 |
2,0674 |
2,0931 |
2,1190 |
2,1321 |
2,1452 |
2,1584 |
2,1716 |
2,1848 |
2,1981 |
|
2 |
0,66667 |
1,0000 |
1,1349 |
1,2071 |
1,2519 |
1,2824 |
1,3045 |
1,3213 |
1,3344 |
1,3450 |
1,3610 |
1,3771 |
1,3933 |
1,4014 |
1,4096 |
1,4178 |
1,4261 |
1,4344 |
1,4427 |
|
3 |
0,58506 |
0,88110 |
1,0000 |
1+,0632 |
1,1024 |
1,1289 |
1,1482 |
1,1627 |
1,1741 |
1,1833 |
1,1972 |
1,2111 |
1,2252 |
1,2322 |
1,2393 |
1,2464 |
1,2536 |
1,2608 |
1,2680 |
|
4 |
0,54863 |
0,82843 |
0,94054 |
1,0000 |
1,0367 |
1,0617 |
1,0797 |
1,0933 |
1,1040 |
1,1126 |
1,1255 |
1,1386 |
1,1517 |
1,1583 |
1,1649 |
1,1716 |
1,1782 |
1,1849 |
1,1916 |
|
5 |
0,52807 |
0,79877 |
0,90715 |
0,96456 |
1,0000 |
1,0240 |
1,0414 |
1,0545 |
1,0648 |
1,0730 |
1,0855 |
1,0980 |
1,1106 |
1,1170 |
1,1234 |
1,1297 |
1,1361 |
1,1426 |
1,1490 |
|
6 |
0,51489 |
0,77976 |
0,88578 |
0,94191 |
0,97654 |
1,0000 |
1,0169 |
1,0298 |
1,0398 |
1,0478 |
1,0600 |
1,0722 |
1,0845 |
1,0907 |
1,0969 |
1,1031 |
1,1093 |
1,1156 |
1,1219 |
|
7 |
0,50572 |
0,76655 |
0,87095 |
0,92619 |
0,96026 |
0,98334 |
1,0000 |
1,0126 |
1,0224 |
1,0304 |
1,0423 |
1,0543 |
1,0664 |
1,0724 |
1,0785 |
1,0846 |
1,0908 |
1,0969 |
1,1031 |
|
8 |
0,49898 |
0,75683 |
0,86004 |
0,91464 |
0,94831 |
0,97111 |
0,98757 |
1,0000 |
1,0097 |
1,0175 |
1,0293 |
1,0412 |
1,0531 |
1,0591 |
1,0651 |
1,0711 |
1,0771 |
1,0832 |
1,0893 |
|
9 |
0,49382 |
0,74938 |
0,85168 |
0,90580 |
0,93916 |
0,96175 |
0,97805 |
0,99037 |
1,0000 |
1,0077 |
1,0194 |
1,0311 |
1,0429 |
1,0489 |
1,0548 |
1,0608 |
1,0667 |
1,0727 |
1,0788 |
|
10 |
0,48973 |
0,74349 |
0,84508 |
0,89882 |
0,93193 |
0,95436 |
0,97054 |
0,98276 |
0,99232 |
1,0000 |
1,0116 |
1,0232 |
1,0349 |
1,0408 |
1,0467 |
1,0526 |
1,0585 |
1,0645 |
1,0705 |
|
11 |
0,48644 |
0,73872 |
0,83973 |
0,89316 |
0,92608 |
0,94837 |
0,96445 |
0,97661 |
0,98610 |
0,99373 |
1,0052 |
1,0168 |
1,0284 |
1,0343 |
1,0401 |
1,0460 |
1,0519 |
1,0578 |
1,0637 |
|
12 |
0,48369 |
0,73477 |
0,83530 |
0,88848 |
0,92124 |
0,94342 |
0,95943 |
0,97152 |
0,98097 |
0,98856 |
1,0000 |
1,0115 |
1,0231 |
1,0289 |
1,0347 |
1,0405 |
1,0464 |
1,0523 |
1,0582 |
|
13 |
0,48141 |
0,73145 |
0,83159 |
0,88454 |
0,91718 |
0,93926 |
0,95520 |
0,96724 |
0,97665 |
0,98421 |
0,99560 |
1,0071 |
1,0186 |
1,0243 |
1,0301 |
1,0360 |
1,0418 |
1,0476 |
1,0535 |
|
14 |
0,47944 |
0,72862 |
0,82842 |
0,88119 |
0,91371 |
0,93573 |
0,95161 |
0,96360 |
0,97298 |
0,98051 |
0,99186 |
1,0033 |
1,0147 |
1,0205 |
1,0263 |
1,0321 |
1,0379 |
1,0437 |
1,0495 |
|
15 |
0,47775 |
0,72619 |
0,82569 |
0,87830 |
0,91073 |
0,93627 |
0,94850 |
0,96046 |
0,96981 |
0,97732 |
0,98863 |
1,0000 |
1,0114 |
1,0172 |
1,0229 |
1,0287 |
1,0345 |
1,0403 |
1,0461 |
|
16 |
0,47628 |
0,72406 |
0,82330 |
0,87578 |
0,90812 |
0,93001 |
0,94580 |
0,95773 |
0,96705 |
0,97454 |
0,98582 |
0,99716 |
1,0086 |
1,0143 |
1,0200 |
1,0258 |
1,0315 |
1,0373 |
1,0431 |
|
17 |
0,47499 |
0,72219 |
0,82121 |
0,87357 |
0,90584 |
0,92767 |
0,94342 |
0,95532 |
0,96462 |
0,97203 |
0,98334 |
0,99466 |
1,0060 |
1,0117 |
1,0174 |
1,0232 |
1,0289 |
1,0347 |
1,0405 |
|
18 |
0,47385 |
0,72053 |
0,81936 |
0,87161 |
0,90381 |
0,92560 |
0,94132 |
0,95319 |
0,96247 |
0,96993 |
0,98116 |
0,99245 |
1,0038 |
1,0095 |
1,0152 |
1,0209 |
1,0267 |
1,0324 |
1,0382 |
|
19 |
0,47284 |
0,71906 |
0,81771 |
0,86987 |
0,90200 |
0,92375 |
0,93944 |
0,95129 |
0,96056 |
0,96800 |
0,97920 |
0,99047 |
1,0018 |
1,0075 |
1,0132 |
1,0189 |
1,0246 |
1,0304 |
1,0361 |
|
20 |
0,47192 |
0,71773 |
0,81621 |
0,86830 |
0,90038 |
0,92210 |
0,93776 |
0,94959 |
0,95884 |
0,96626 |
0,97746 |
0,98870 |
1,0000 |
1,0057 |
1,0114 |
1,0171 |
1,0228 |
1,0285 |
1,0343 |
|
21 |
0,47108 |
0,71653 |
0,81487 |
0,86688 |
0,89891 |
0,92060 |
0,93624 |
0,94805 |
0,95728 |
0,96470 |
0,97587 |
0,98710 |
0,99838 |
1,0040 |
1,0097 |
1,0154 |
1,0211 |
1,0268 |
1,0326 |
|
22 |
0,47033 |
0,71545 |
0,81365 |
0,86559 |
0,89759 |
0,91924 |
0,93486 |
0,94665 |
0,95588 |
0,96328 |
0,97444 |
0,98565 |
0,99692 |
1,0026 |
1,0082 |
1,0139 |
1,0196 |
1,0253 |
1,0311 |
|
23 |
0,46965 |
0,71446 |
0,81255 |
0,86442 |
0,89638 |
0,91800 |
0,93360 |
0,94538 |
0,95459 |
0,96199 |
0,97313 |
0,98433 |
0,99558 |
1,0012 |
1,0069 |
1,0126 |
1,0183 |
1,0240 |
1,0297 |
|
24 |
0,46902 |
0,71356 |
0,81153 |
0,86335 |
0,89527 |
0,91687 |
0,93245 |
0,94422 |
0,95342 |
0,96081 |
0,97194 |
0,98312 |
0,99436 |
1,0000 |
1,0057 |
1,0113 |
1,0170 |
1,0227 |
1,0284 |
|
25 |
0,46844 |
0,71272 |
0,81061 |
0,86236 |
0,89425 |
0,91583 |
0,93140 |
0,94315 |
0,95234 |
0,95972 |
0,97084 |
0,98201 |
0,99324 |
0,99887 |
1,0045 |
1,0102 |
1,0159 |
1,0215 |
1,0273 |
|
26 |
0,46793 |
0,71195 |
0,80975 |
0,86145 |
0,89331 |
0,91487 |
0,93042 |
0,94217 |
0,95135 |
0,95872 |
0,96983 |
0,98099 |
0,99220 |
0,99783 |
1,0035 |
1,0091 |
1,0148 |
1,0205 |
1,0262 |
|
27 |
0,46744 |
0,71124 |
0,80894 |
0,86061 |
0,89244 |
0,91399 |
0,92952 |
0,94126 |
0,95044 |
0,95779 |
0,96889 |
0,98004 |
0,99125 |
0,99687 |
1,0025 |
1,0082 |
1,0138 |
1,0195 |
1,0252 |
|
28 |
0,46697 |
0,71059 |
0,80820 |
0,85983 |
0,89164 |
0,91317 |
0,92869 |
0,94041 |
0,94958 |
0,95694 |
0,96802 |
0,97917 |
0,99036 |
0,99598 |
1,0016 |
1,0073 |
1,0129 |
1,0186 |
1,0243 |
|
29 |
0,46654 |
0,70999 |
0,80753 |
0,85911 |
0,89089 |
0,91241 |
0,92791 |
0,93963 |
0,94879 |
0,95614 |
0,96722 |
0,97835 |
0,98954 |
0,99515 |
1,0008 |
1,0064 |
1,0121 |
1,0177 |
1,0234 |
|
30 |
0,46616 |
0,70941 |
0,80689 |
0,85844 |
0,89019 |
0,91169 |
0,92719 |
0,93889 |
0,94805 |
0,95540 |
0,96647 |
0,97759 |
0,98877 |
0,99438 |
1,0000 |
1,0056 |
1,0113 |
1,0170 |
1,0226 |
|
40 |
0,46330 |
0,70531 |
0,80228 |
0,85357 |
0,88516 |
0,90654 |
0,92197 |
0,93361 |
0,94272 |
0,95003 |
0,96104 |
0,97211 |
0,98323 |
0,98880 |
0,99440 |
1,0000 |
1,0056 |
1,0113 |
1,0169 |
|
60 |
0,46053 |
0,70122 |
0,79770 |
0,84873 |
0,88017 |
0,90144 |
0,91679 |
0,92838 |
0,93743 |
0,94471 |
0,95566 |
0,96667 |
0,97773 |
0,98328 |
0,98884 |
0,99411 |
1,0000 |
1,0056 |
1,0112 |
|
120 |
0,45774 |
0,69717 |
0,79314 |
0,84392 |
0,87521 |
0,89637 |
0,91164 |
0,92318 |
0,93218 |
0,93943 |
0,95032 |
0,96128 |
0,97228 |
0,97780 |
0,98333 |
0,98887 |
0,99443 |
1,0000 |
1,0056 |
|
¥ |
0,45494 |
0,69315 |
0,78866 |
0,83918 |
0,87029 |
0,89135 |
0,90654 |
0,91802 |
0,92698 |
0,93418 |
0,94503 |
0,95593 |
0,96687 |
0,97236 |
0,97787 |
0,98339 |
0,98891 |
0,99445 |
1,0000 |
(Измененная редакция, Изм. №
1).
ТАБЛИЦА Г.2 - КВАНТИЛИ F-РАСПРЕДЕЛЕНИЯ
УРОВНЯ a = 0,75
|
v2 |
Квантили F-распределения уровня a = 0,75 для степени свободы v1 |
||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
12 |
15 |
20 |
24 |
30 |
40 |
60 |
120 |
¥ |
|
|
1 |
5,8285 |
7,5000 |
8,1999 |
8,5810 |
8,8198 |
8,9833 |
9,1021 |
9,1922 |
9,2631 |
9,3202 |
9,4064 |
9,4934 |
9,5813 |
9,6255 |
9,6698 |
9,7144 |
9,7591 |
9,8041 |
9,8492 |
|
2 |
2,5714 |
3,0000 |
3,1534 |
3,2320 |
3,2799 |
3,3121 |
3,3352 |
3,3526 |
3,3661 |
3,3770 |
3,3934 |
3,4098 |
3,4263 |
3,4345 |
3,4428 |
3,4511 |
3,4594 |
3,4677 |
3,4761 |
|
3 |
2,0239 |
2,2798 |
2,3555 |
2,3901 |
2,4095 |
2,4218 |
2,4302 |
2,4364 |
2,4410 |
2,4447 |
2,4500 |
2,4552 |
2,4602 |
2,4626 |
2,4650 |
2,4674 |
2,4697 |
2,4720 |
2,4742 |
|
4 |
1,8074 |
2,0000 |
2,0467 |
2,0642 |
2,0723 |
2,0766 |
2,0790 |
2,0805 |
2,0814 |
2,0820 |
2,0826 |
2,0829 |
2,0828 |
2,0827 |
2,0825 |
2,0821 |
2,0817 |
2,0812 |
2,0806 |
|
5 |
1,6925 |
1,8528 |
1,8843 |
1,8927 |
1,8947 |
1,8945 |
1,8935 |
1,8923 |
1,8911 |
1,8899 |
1,8877 |
1,8851 |
1,8820 |
1,8802 |
1,8784 |
1,8763 |
1,8742 |
1,8719 |
1,8694 |
|
6 |
1,6214 |
1,7622 |
1,7844 |
1,7872 |
1,7852 |
1,7821 |
1,7789 |
1,7760 |
1,7733 |
1,7708 |
1,7668 |
1,7621 |
1,7569 |
1,7540 |
1,7510 |
1,7477 |
1,7443 |
1,7407 |
1,7368 |
|
7 |
1,5732 |
1,7010 |
1,7169 |
1,7157 |
1,7111 |
1,7059 |
1,7011 |
1,6969 |
1,6931 |
1,6898 |
1,6843 |
1,6781 |
1,6712 |
1,6675 |
1,6635 |
1,6593 |
1,6548 |
1,6502 |
1,6452 |
|
8 |
1,5384 |
1,6569 |
1,6683 |
1,6642 |
1,6575 |
1,6508 |
1,6448 |
1,6396 |
1,6350 |
1,6310 |
1,6244 |
1,6170 |
1,6088 |
1,6043 |
1,5996 |
1,5945 |
1,5892 |
1,5836 |
1,5777 |
|
9 |
1,5121 |
1,6236 |
1,6315 |
1,6253 |
1,6170 |
1,6091 |
1,6022 |
1,5961 |
1,5909 |
1,5863 |
1,5788 |
1,5705 |
1,5611 |
1,5560 |
1,5506 |
1,5450 |
1,5389 |
1,5325 |
1,5257 |
|
10 |
1,4915 |
1,5975 |
1,6028 |
1,5949 |
1,5863 |
1,5765 |
1,5688 |
1,5621 |
1,5563 |
1,5513 |
1,5430 |
1,5338 |
1,5235 |
1,5179 |
1,5119 |
1,5056 |
1,4990 |
1,4919 |
1,4843 |
|
11 |
1,4749 |
1,5767 |
1,5798 |
1,5794 |
1,5598 |
1,5502 |
1,5418 |
1,5346 |
1,5284 |
1,5230 |
1,5140 |
1,5041 |
1,4930 |
1,4869 |
1,4805 |
1,4737 |
1,4664 |
1,4587 |
1,4504 |
|
12 |
1,4613 |
1,5595 |
1,5609 |
1,5503 |
1,5389 |
1,5286 |
1,5197 |
1,5120 |
1,5054 |
1,4996 |
1,4902 |
1,4796 |
1,4678 |
1,4613 |
1,4544 |
1,4471 |
1,4393 |
1,4310 |
1,4221 |
|
13 |
1,4500 |
1,5452 |
1,5451 |
1,5336 |
1,5214 |
1,5105 |
1,5011 |
1,4931 |
1,4861 |
1,4801 |
1,4701 |
1,4590 |
1,4465 |
1,4397 |
1,4324 |
1,4247 |
1,4164 |
1,4075 |
1,3980 |
|
14 |
1,4403 |
1,5331 |
1,5317 |
1,5194 |
1,5066 |
1,4952 |
1,4854 |
1,4770 |
1,4697 |
1,4634 |
1,4530 |
1,4414 |
1,4284 |
1,4212 |
1,4136 |
1,4055 |
1,3967 |
1,3874 |
1,3772 |
|
15 |
1,4321 |
1,5227 |
1,5202 |
1,5071 |
1,4938 |
1,4820 |
1,4718 |
1,4631 |
1,4556 |
1,4491 |
1,4383 |
1,4263 |
1,4127 |
1,4052 |
1,3973 |
1,3888 |
1,3796 |
1,3698 |
1,3591 |
|
16 |
1,4249 |
1,5137 |
1,5103 |
1,4965 |
1,4827 |
1,4705 |
1,4601 |
1,4511 |
1,4433 |
1,4366 |
1,4255 |
1,4130 |
1,3990 |
1,3913 |
1,3830 |
1,3742 |
1,3646 |
1,3543 |
1,3432 |
|
17 |
1,4186 |
1,5057 |
1,5015 |
1,4873 |
1,4730 |
1,4605 |
1,4497 |
1,4405 |
1,4325 |
1,4256 |
1,4142 |
1,4014 |
1,3869 |
1,3790 |
1,3704 |
1,3613 |
1,3514 |
1,3406 |
1,3290 |
|
18 |
1,4130 |
1,4988 |
1,4938 |
1,4790 |
1,4644 |
1,4516 |
1,4406 |
1,4312 |
1,4230 |
1,4159 |
1,4042 |
1,3911 |
1,3762 |
1,3680 |
1,3592 |
1,3497 |
1,3395 |
1,3284 |
1,3162 |
|
19 |
1,4081 |
1,4925 |
1,4870 |
1,4717 |
1,4568 |
1,4437 |
1,4325 |
1,4228 |
1,4145 |
1,4073 |
1,3953 |
1,3819 |
1,3666 |
1,3582 |
1,3492 |
1,3394 |
1,3289 |
1,3174 |
1,3048 |
|
20 |
1,4037 |
1,4870 |
1,4808 |
1,4652 |
1,4500 |
1,4366 |
1,4252 |
1,4153 |
1,4069 |
1,3995 |
1,3873 |
1,3736 |
1,3580 |
1,3494 |
1,3401 |
1,3301 |
1,3193 |
1,3074 |
1,2943 |
|
21 |
1,3997 |
1,4820 |
1,4753 |
1,4593 |
1,4438 |
1,4302 |
1,4186 |
1,4086 |
1,4000 |
1,3925 |
1,3801 |
1,3661 |
1,3502 |
1,3414 |
1,3319 |
1,3217 |
1,3105 |
1,2983 |
1,2848 |
|
22 |
1,3961 |
1,4774 |
1,4703 |
1,4540 |
1,4382 |
1,4244 |
1,4126 |
1,4025 |
1,3937 |
1,3861 |
1,3735 |
1,3593 |
1,3431 |
1,3341 |
1,3245 |
1,3140 |
1,3025 |
1,2900 |
1,2761 |
|
23 |
1,3928 |
1,4733 |
1,4657 |
1,4491 |
1,4331 |
1,4191 |
1,4072 |
1,3969 |
1,3880 |
1,3803 |
1,3675 |
1,3531 |
1,3366 |
1,3275 |
1,3176 |
1,3069 |
1,2952 |
1,2824 |
1,2681 |
|
24 |
1,3898 |
1,4695 |
1,4615 |
1,4447 |
1,4285 |
1,4143 |
1,4022 |
1,3918 |
1,3828 |
1,3750 |
1,3621 |
1,3474 |
1,3307 |
1,3214 |
1,3113 |
1,3004 |
1,2885 |
1,2754 |
1,2607 |
|
25 |
1,3870 |
1,4661 |
1,4577 |
1,4406 |
1,4242 |
1,4099 |
1,3976 |
1,3871 |
1,3780 |
1,3701 |
1,3570 |
1,3422 |
1,3252 |
1,3158 |
1,3056 |
1,2945 |
1,2823 |
1,2689 |
1,2538 |
|
26 |
1,3845 |
1,4629 |
1,4542 |
1,4368 |
1,4203 |
1,4058 |
1,3935 |
1,3828 |
1,3737 |
1,3656 |
1,3524 |
1,3374 |
1,3202 |
1,3106 |
1,3002 |
1,2889 |
1,2765 |
1,2628 |
1,2474 |
|
27 |
1,3,S22 |
1,4600 |
1,4510 |
1,4334 |
1,4166 |
1,4021 |
1,3896 |
1,3788 |
1,3696 |
1,3615 |
1,3481 |
1,3329 |
1,3155 |
1,3058 |
1,2953 |
1,2838 |
1,2712 |
1,2572 |
1,2414 |
|
28 |
1,3800 |
1,4573 |
1,4480 |
1,4302 |
1,4133, |
1,3986 |
1,3860 |
1,3752 |
1,3658 |
1,3576 |
1,3441 |
1,3288 |
1,3,112 |
1,3013 |
1,2906 |
1,2790 |
1,2662 |
1,2519 |
1,2358 |
|
29 |
1,3780 |
1,4547 |
1,4452 |
1,4272 |
1,4102 |
1,3953 |
1,3826 |
1,3717 |
1,3623 |
1,3541 |
1,3404 |
1,3249 |
1,3071 |
1,2971 |
1,2863 |
1,2745 |
1,2615 |
1,2470 |
1,2306 |
|
30 |
1,3761 |
1,4524 |
1,4426 |
1,4244 |
1,4073 |
1,3923 |
1,3795 |
1,3685 |
1,3590 |
1,3507 |
1,3369 |
1,3213 |
1,3033 |
1,2933 |
1,2823 |
1,2703 |
1,2571 |
1,2424 |
1,2256 |
|
40 |
1,3626 |
1,4355 |
1,4239 |
1,4045 |
1,3863 |
1,3706 |
1,3571 |
1,3455 |
1,3354 |
1,3266 |
1,3119 |
1,2952 |
1,2758 |
1,2649 |
1,2529 |
1,2397 |
1,2249 |
1,2080 |
1,1883 |
|
60 |
1,3493 |
1,4188 |
1,4055 |
1,3848 |
1,3657 |
1,3491 |
1,3349 |
1,3226 |
1,3119 |
1,3026 |
1,2870 |
1,2691 |
1,2481 |
1,2361 |
1,2229 |
1,2081 |
1,1912 |
1,1715 |
1,1474 |
|
120 |
1,3362 |
1,4024 |
1,3873 |
1,3654 |
1,3453 |
1,3278 |
1,3128 |
1,2999 |
1,2886 |
1,2787 |
1,2621 |
1,2428 |
1,2200 |
1,2068 |
1,1921 |
1,1752 |
1,1555 |
1,1314 |
1,0987 |
|
¥ |
1,3233 |
1,3863 |
1,3694 |
1,3463 |
1,3251 |
1,3068 |
1,2910 |
1,2774 |
1,2654 |
1,2549 |
1,2371 |
1,2163 |
1,1914 |
1,1767 |
1,1600 |
1,1404 |
1,1164 |
1,0838 |
1,0000 |
(Измененная редакция, Изм. №
1).
ТАБЛИЦА Г.3 - КВАНТИЛИ F-РАСПРЕДЕЛЕНИЯ
УРОВНЯ a = 0,999
|
v2 |
Квантили F-распределения уровня a = 0,999 для степени свободы v1 |
||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
12 |
15 |
20 |
24 |
30 |
40 |
60 |
120 |
¥ |
|
|
1 |
405300 |
500000 |
540400 |
562500 |
576400 |
585900 |
592900 |
598100 |
602300 |
605600 |
610700 |
615800 |
620900 |
623500 |
626100 |
628700 |
631300 |
634000 |
636600 |
|
2 |
998,5 |
999,0 |
999,2 |
999,2 |
999,3 |
999,3 |
999,4 |
999,4 |
999,4 |
999,4 |
999,4 |
999,4 |
999,4 |
999,5 |
999,5 |
999,5 |
999,5 |
999,5 |
999,5 |
|
1 |
167,0 |
148,5 |
141,1 |
137,1 |
134,6 |
132,8 |
131,6 |
130,6 |
129,9 |
129,2 |
128,3 |
127,4 |
126,4 |
125,9 |
125,4 |
125,0 |
124,5 |
124,0 |
123,5 |
|
4 |
74,14 |
61,25 |
56,18 |
53,44 |
51,71 |
50,53 |
49,66 |
49,00 |
48,47 |
48,05 |
47,41 |
46,76 |
46,10 |
45,77 |
45,43 |
45,09 |
44,75 |
44,40 |
44,05 |
|
5 |
47,18 |
37,12 |
33,20 |
31,09 |
29,75 |
28,54 |
28,16 |
27,64 |
27,24 |
26,92 |
26,42 |
25,91 |
25,39 |
25,14 |
24,87 |
24,60 |
24,33 |
24,06 |
23,79 |
|
6 |
35,51 |
27,00 |
23,70 |
21,92 |
20,81 |
20,03 |
19,46 |
19,03 |
18,69 |
18,41 |
17,99 |
17,56 |
17,12 |
16,89 |
16,67 |
16,44 |
16,21 |
15,99 |
15,75 |
|
7 |
29,25 |
21,69 |
18,77 |
17,19 |
16,21 |
15,52 |
15,02 |
14,63 |
14,33 |
14,08 |
13,71 |
13,32 |
12,93 |
12,73 |
12,53 |
12,33 |
12,12 |
11,91 |
11,70 |
|
8 |
25,42 |
18,49 |
15,83 |
14,39 |
13,49 |
12,86 |
12,40 |
12,04 |
11,77 |
11,54 |
11,19 |
10,84 |
10,48 |
10,30 |
10,11 |
9,92 |
9,73 |
9,53 |
9,33 |
|
9 |
22,86 |
16,39 |
13,90 |
12,56 |
11,71 |
11,13 |
10,70 |
10,37 |
10,11 |
9,89 |
9,57 |
9,24 |
8,90 |
8,72 |
8,55 |
8,37 |
8,19 |
8,00 |
7,81 |
|
10 |
21,04 |
14,91 |
12,55 |
11,28 |
10,48 |
9,92 |
9,52 |
9,20 |
8,96 |
8,75 |
8,45 |
8,13 |
7,80 |
7,64 |
7,47 |
7,30 |
7,12 |
6,94 |
6,76 |
|
11 |
19,69 |
13,81 |
11,56 |
10,35 |
9,58 |
9,05 |
8,66 |
8,35 |
8,12 |
7,92 |
7,63 |
7,32 |
7,01 |
6,85 |
6,68 |
6,52 |
6,35 |
6,17 |
6,00 |
|
12 |
18,64 |
12,97 |
10,80 |
9,63 |
8,89 |
8,38 |
8,00 |
7,71 |
7,48 |
7,29 |
7,00 |
6,71 |
6,40 |
6,25 |
6,09 |
5,93 |
5,76 |
5,59 |
5,42 |
|
13 |
17,81 |
12,31 |
10,21 |
9,07 |
8,35 |
7,86 |
7,49 |
7,21 |
6,98 |
6,80 |
6,52 |
6,23 |
5,93 |
5,78 |
5,63 |
5,47 |
5,30 |
5,14 |
4,97 |
|
14 |
17,14 |
11,78 |
9,73 |
8,62 |
7,92 |
7,43 |
7,08 |
6,80 |
6,58 |
6,40 |
6,13 |
5,85 |
5,56 |
5,41 |
5,25 |
5,10 |
4,94 |
4,77 |
4,60 |
|
15 |
16,59 |
11,34 |
9,34 |
8,25 |
7,57 |
7,09 |
6,74 |
6,47 |
6,26 |
6,08 |
5,81 |
5,54 |
5,25 |
5,10 |
4,95 |
4,80 |
4,64 |
4,47 |
4,31 |
|
16 |
16,12 |
10,97 |
9,00 |
7,94 |
7,27 |
6,81 |
6,46 |
6,19 |
5,98 |
5,81 |
5,55 |
5,27 |
4,99 |
4,85 |
4,70 |
4,54 |
4,39 |
4,23 |
4,06 |
|
17 |
15,72 |
10,66 |
8,73 |
7,68 |
7,02 |
6,56 |
6,22 |
5,96 |
5,75 |
5,58 |
5,32 |
5,05 |
4,78 |
4,63 |
4,48 |
4,33 |
4,18 |
4,02 |
3,85 |
|
18 |
15,38 |
10,39 |
8,49 |
7,46 |
6,81 |
6,35 |
6,02 |
5,76 |
5,56 |
5,39 |
5,13 |
4,87 |
4,59 |
4,45 |
4,30 |
4,15 |
4,00 |
3,84 |
3,67 |
|
19 |
15,08 |
10,16 |
8,28 |
7,26 |
6,62 |
6,18 |
5,85 |
5,59 |
5,39 |
5,22 |
4,97 |
4,70 |
4,43 |
4,29 |
4,14 |
3,99 |
3,84 |
3,68 |
3,51 |
|
20 |
14,82 |
9,95 |
8,10 |
7,10 |
6,46 |
6,02 |
5,69 |
5,44 |
5,24 |
5,08 |
4,82 |
4,56 |
4,29 |
4,15 |
4,00 |
3,86 |
3,70 |
3,54 |
3,38 |
|
21 |
14,59 |
9,77 |
7,94 |
6,95 |
6,32 |
5,88 |
5,56 |
5,31 |
5,11 |
4,95 |
4,70 |
4,44 |
4,17 |
4,03 |
3,88 |
3,74 |
3,58 |
3,42 |
3,26 |
|
22 |
14,38 |
9,61 |
7,80 |
6,81 |
6,19 |
5,76 |
5,44 |
5,19 |
4,99 |
4,83 |
4,58 |
4,33 |
4,06 |
3,92 |
3,78 |
3,63 |
3,48 |
3,32 |
3,15 |
|
23 |
14,19 |
9,47 |
7,67 |
6,69 |
6,08 |
5,65 |
5,33 |
5,09 |
4,89 |
4,73 |
4,48 |
4,23 |
4,23 |
3,82 |
3,68 |
3,53 |
3,38 |
3,22 |
3,05 |
|
24 |
14,03 |
9,34 |
7,55 |
6,59 |
5,98 |
5,55 |
5,23 |
4,99 |
4,80 |
4,64 |
4,39 |
4,14 |
3,87 |
3,74 |
3,59 |
3,45 |
3,29 |
3,14 |
2,97 |
|
25 |
13,88 |
9,22 |
7,45 |
6,49 |
5,88 |
5,46 |
5,15 |
4,91 |
4,71 |
4,56 |
4,31 |
4,06 |
3,79 |
3,66 |
3,52 |
3,37 |
3,22 |
3,06 |
2,89 |
|
26 |
13,74 |
9,12 |
7,36 |
6,41 |
5,80 |
5,38 |
5,07 |
4,83 |
4,64 |
4,48 |
4,24 |
3,99 |
3,72 |
3,59 |
3,44 |
3,30 |
3,15 |
2,99 |
2,82 |
|
27 |
13,61 |
9,02 |
7,27 |
6,33 |
5,73 |
5,31 |
5,00 |
4,76 |
4,57 |
4,41 |
4,17 |
3,92 |
3,66 |
3,52 |
3,38 |
3,23 |
3,08 |
2,92 |
2,75 |
|
28 |
13,50 |
8,93 |
7,19 |
6,25 |
5,66 |
5,24 |
4,93 |
4,69 |
4,50 |
4,35 |
4,11 |
3,86 |
3,60 |
3,46 |
3,32 |
3,18 |
3,02 |
2,86 |
2,69 |
|
29 |
13,39 |
8,85 |
7,12 |
6,19 |
5,59 |
5,18 |
4,87 |
4,64 |
4,45 |
4,29 |
4,05 |
3,80 |
3,54 |
3,41 |
3,27 |
3,12 |
2,97 |
2,81 |
2,64 |
|
30 |
13,29 |
8,77 |
7,05 |
6,12 |
5,53 |
5,12 |
4,82 |
4,58 |
4,39 |
4,24 |
4,00 |
3,75 |
3,49 |
3,36 |
3,22 |
3,07 |
2,92 |
2,76 |
2,59 |
|
40 |
12,61 |
8,25, |
6,60 |
5,70 |
5,13 |
4,73 |
4,44 |
4,21 |
4,02 |
3,87 |
3,64 |
3,40 |
3,15 |
3,01 |
2,87 |
2,73 |
2,57 |
2,41 |
2,23 |
|
60 |
11,97 |
7,76 |
6,17 |
5,31 |
4,76 |
4,37 |
4,09 |
3,87 |
3,69 |
3,54 |
3,31 |
3,08 |
2,83 |
2,69 |
2,55 |
2,41 |
2,25 |
2,08 |
1,89 |
|
120 |
11,38 |
7,32 |
5,79 |
4,95 |
4,42 |
4,04 |
3,77 |
3,55 |
3,38 |
3,24 |
3,02 |
2,78 |
2,53 |
2,40 |
2,26 |
2,11 |
1,95 |
1,76 |
1,54 |
|
¥ |
10,83 |
6,91 |
5,42 |
4,62 |
4,10 |
3,74 |
3,47 |
3,27 |
3,10 |
2,96 |
2,74 |
2,51 |
2,27 |
2,13 |
1,99 |
1,84 |
1,66 |
1,45 |
1,00 |
(Измененная редакция, Изм. №
1).
ТАБЛИЦА Г.4 - КВАНТИЛИ F-РАСПРЕДЕЛЕНИЯ
УРОВНЯ а = 0,9995
|
v2 |
Квантили F-распределения уровня a = 0,9995 для степени свободы v1 |
|||||||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
15 |
20 |
24 |
30 |
40 |
50 |
60 |
100 |
120 |
200 |
500 |
03 |
|
|
1 |
1620000 |
2000000 |
2160000 |
2250000 |
2310000 |
2340000 |
2370000 |
2390000 |
2410000 |
2420000 |
2430000 |
2440000 |
2460000 |
2480000 |
2490000 |
2500000 |
2510000 |
2520000 |
2520000 |
2530000 |
2530000 |
2530000 |
2540000 |
2540000 |
|
2 |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
|
3 |
266 |
237 |
225 |
218 |
214 |
211 |
209 |
208 |
207 |
206 |
204 |
204 |
203 |
201 |
200 |
199 |
199 |
198 |
198 |
197 |
197 |
197 |
196 |
196 |
|
4 |
106 |
87,4 |
80,1 |
76,1 |
73,6 |
71,9 |
70,6 |
69,7 |
68,9 |
68,3 |
67,8 |
67,4 |
66,5 |
65,5 |
65,1 |
64,6 |
64,1 |
63,8 |
63,6 |
63,2 |
63,1 |
62,9 |
62,7 |
62,6 |
|
5 |
63,6 |
49,S |
44,4 |
41,5 |
39,7 |
38,5 |
37,6 |
36,9 |
36,4 |
35,9 |
35,6 |
35,2 |
34,6 |
33,9 |
33,5 |
33,1 |
32,7 |
32,5 |
32,3 |
32,1 |
32,0 |
31,8 |
31,7 |
31,6 |
|
6 |
46,1 |
34,8 |
30,4 |
28,1 |
26,6 |
25,6 |
24,9 |
24,3 |
23,9 |
23,5 |
23,2 |
23,0 |
22,4 |
21,9 |
21,7 |
21,4 |
21,1 |
20,9 |
20,7 |
20,5 |
20,4 |
20,3 |
20,2, |
20,1 |
|
7 |
37,0 |
27,2 |
23,5 |
21,4 |
20,2 |
19,3 |
18,7 |
18,2 |
17,8 |
17,5 |
17,2 |
17,0 |
16,5 |
16,0 |
15,7 |
15,5 |
15,2 |
15,1 |
15,0 |
14,7 |
14,7 |
14,6 |
14,5 |
14,4 |
|
8 |
31,6 |
22,8 |
19,4 |
17,6 |
16,4 |
15,7 |
15,1 |
14,6 |
14,3 |
14,0 |
13,8 |
13,6 |
13,1 |
12,7 |
12,5 |
12,2 |
12,0 |
11,8 |
11,8 |
11,6 |
11,5 |
11,4 |
11,4 |
11,3 |
|
9 |
28,0 |
19,9 |
16,8 |
15,1 |
14,1 |
13,3 |
12,8 |
12,4 |
12,1 |
11,8 |
11,6 |
11,4 |
11,0 |
10,6 |
10,4 |
10,2 |
9,94 |
9,80 |
9,1 |
9,53 |
9,49 |
9,40 |
9,32 |
9,26 |
|
10 |
25,5 |
17,9 |
15,0 |
13,4 |
12,4 |
11,8 |
11,3 |
10,9 |
10,6 |
10,3 |
10,1 |
9,93 |
9,56 |
9,16 |
8,96 |
8,75 |
8,54 |
8,42 |
8,33 |
8,16 |
8,12 |
8,04 |
7,96 |
7,90 |
|
11 |
23,6 |
16,4 |
13,6 |
12,2 |
11,2 |
10,6 |
10,1 |
9,76 |
9,48 |
9,24 |
9,04 |
8,88 |
8,52 |
8,14 |
7,94 |
7,75 |
7,55 |
7,43 |
7,35 |
7,18 |
7,14 |
7,06 |
6,98 |
6,93 |
|
12 |
22,2 |
15,3 |
12,7 |
11,2 |
10,4 |
9,74 |
9,28 |
8,94 |
8,66 |
8,43 |
8,24 |
8,08 |
7,74 |
7,37 |
7,18 |
7,00 |
6,80 |
6,68 |
6,61 |
6,45 |
6,41 |
6,33 |
6,25 |
6,20 |
|
15 |
19,5 |
13,2 |
10,8 |
9,48 |
8,66 |
8,10 |
7,68 |
7,36 |
7,11 |
6,91 |
6,75 |
6,60 |
6,27 |
5,93 |
5,75 |
5,58 |
5,40 |
5,29 |
5,21 |
5,06 |
5,02 |
4,94 |
4,87 |
4,83 |
|
20 |
17,2 |
11,4 |
9,20 |
8,02 |
7,28 |
6,76 |
6,38 |
6,08 |
5,85 |
5,66 |
5,51 |
5,38 |
5,07 |
4,75 |
4,58 |
4,42 |
4,24 |
4,15 |
4,07 |
3,93 |
3,90 |
3,82 |
3,75 |
3,70 |
|
24 |
16,2 |
10,6 |
8,52 |
7,39 |
6,68 |
6,18 |
5,82 |
5,54 |
5,31 |
5,13 |
4,98 |
4,85 |
4,55 |
4,25 |
4,09 |
3,93 |
3,76 |
3,66 |
3,59 |
3,44 |
3,41 |
3,33 |
3,27 |
3,22 |
|
30 |
15,2 |
9,90 |
7,90 |
6,82 |
6,14 |
5,66 |
5,31 |
5,04 |
4,82 |
4,65 |
4,51 |
4,38 |
4,10 |
3,80 |
3,65 |
3,48 |
3,32 |
3,22 |
3,15 |
3,00 |
2,97 |
2,89 |
2,82 |
2,78 |
|
40 |
14,4 |
9,25 |
7,33 |
6,30 |
5,64 |
5,19 |
4,85 |
4,59 |
4,38 |
4,21 |
4,07 |
3,95 |
3,68 |
3,39 |
3,24 |
3,08 |
2,92 |
2,82 |
2,74 |
2,60 |
2,57 |
2,49 |
2,41 |
2,37 |
|
60 |
13,6 |
8,65 |
6,81 |
5,32 |
5,20 |
4,76 |
4,44 |
4,18 |
3,98 |
3,82 |
3,69 |
3,57 |
3,30 |
3,02 |
2,87 |
2,71 |
2,55 |
2,45 |
2,38 |
2,23 |
2,19 |
2,11 |
2,03 |
1,98 |
|
120 |
12,8 |
8,10 |
6,34 |
5,39 |
4,79 |
4,37 |
4,07 |
3,82 |
3,63 |
3,47 |
3,34 |
3,22 |
3,96 |
2,67 |
2,53 |
2,38 |
2,21 |
2,11 |
2,01 |
1,88 |
1,84 |
1,75 |
1,67 |
1,60 |
|
¥ |
12,1 |
7,60 |
5,91 |
5,00 |
4,42 |
4,02 |
3,72 |
3,48 |
3,30 |
3,14 |
3,02 |
2,90 |
2,65 |
2,37 |
2,22 |
2,07 |
1,91 |
1,79 |
1,71 |
1,53 |
1,48 |
1,36 |
1,22 |
1,00 |
(Измененная редакция, Изм. №
1).
ТАБЛИЦА Г.5 - КВАНТИЛИ F-РАСПРЕДЕЛЕНИЯ
УРОВНЯ a = 0,995
|
v2 |
Квантили F-распределения уровня a = 0,995 для степени свободы v1 |
||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
12 |
15 |
20 |
24 |
30 |
40 |
60 |
120 |
¥ |
|
|
1 |
16211 |
20000 |
21615 |
22500 |
23056 |
23437 |
23715 |
23925 |
24091 |
24224 |
24426 |
24630 |
24836 |
24940 |
25044 |
25148 |
25253 |
25359 |
25465 |
|
2 |
198,50 |
199,00 |
199,17 |
199,25 |
199,30 |
199,33 |
199,36 |
199,37 |
199,39 |
199,40 |
199,42 |
199,43 |
199,45 |
199,46 |
199,47 |
199,47 |
199,48 |
199,49 |
199,51 |
|
3 |
55,552 |
49,799 |
47,467 |
46,195 |
45,392 |
44,838 |
44,434 |
44,126 |
43,882 |
43,686 |
43,387 |
43,085 |
42,778 |
42,622 |
42,466 |
42,308 |
42,149 |
41,989 |
41,829 |
|
4 |
31,333 |
26,284 |
24,259 |
23,155 |
22,456 |
21,975 |
21,622 |
21,352 |
21,139 |
20,967 |
20,705 |
20,438 |
20,167 |
20,030 |
19,892 |
19,752 |
19,611 |
19,468 |
19,325 |
|
5 |
22,785 |
18,314 |
16,530 |
15,556 |
14,940 |
14,513 |
14,200 |
13,961 |
13,772 |
13,618 |
13,384 |
13,146 |
12,903 |
12,780 |
12,656 |
12,530 |
12,402 |
12,274 |
12,144 |
|
6 |
18,635 |
14,544 |
12,917 |
12,028 |
11,464 |
11,073 |
10,786 |
10,566 |
10,391 |
10,250 |
10,034 |
9,8140 |
9,5888 |
9,4741 |
9,3583 |
9,2408 |
9,1219 |
9,0015 |
8,8793 |
|
7 |
16,236 |
12,404 |
10,882 |
10,050 |
9,5221 |
9,1554 |
8,8854 |
8,6781 |
8,5138 |
8,3803 |
8,1764 |
7,9678 |
7,7540 |
7,6450 |
7,5345 |
7,4225 |
7,3088 |
7,1933 |
7,0760 |
|
8 |
14,688 |
11,042 |
9,5965 |
8,8051 |
8,3018 |
7,9520 |
7,6942 |
7,4960 |
7,3386 |
7,2107 |
7,0149 |
6,8143 |
6,6082 |
6,5029 |
6,3961 |
6,2875 |
6,1772 |
6,0649 |
5,9505 |
|
9 |
13,614 |
10,107 |
8,7171 |
7,9559 |
7,4711 |
7,1338 |
6,8849 |
6,6933 |
6,5411 |
6,4171 |
6,2274 |
6,0325 |
5,8318 |
5,7292 |
5,6248 |
5,5186 |
5,4104 |
5,3001 |
5,1875 |
|
10 |
12,826 |
9,4270 |
8,0807 |
7,3428 |
6,8723 |
6,5446 |
6,3025 |
6,1159 |
5,9676 |
5,8467 |
5,6613 |
5,4707 |
5,2740 |
5,1732 |
5,0705 |
4,9659 |
4,8592 |
4,7501 |
4,6385 |
|
11 |
12,226 |
8,9122 |
7,6004 |
6,8809 |
6,4217 |
6,1015 |
5,8648 |
5,6821 |
5,5368 |
5,4182 |
5,2363 |
5,0489 |
4,8552 |
4,7557 |
4,6543 |
4,5508 |
4,4450 |
4,3367 |
4,2256 |
|
12 |
11,754 |
8,5096 |
7,2258 |
6,5211 |
6,0711 |
5,7570 |
5,5245 |
5,3451 |
5,2021 |
5,0855 |
4,9063 |
4,7214 |
4,5299 |
4,4315 |
4,3309 |
4,2282 |
4,1229 |
4,0149 |
3,9039 |
|
13 |
11,374 |
8,1865 |
6,9257 |
6,2335 |
5,7910 |
5,4819 |
5,2529 |
5,0761 |
4,9351 |
4,8199 |
4,6429 |
4,4600 |
4,2703 |
4,1726 |
4,0727 |
3,9704 |
3,8665 |
3,7577 |
3,6465 |
|
14 |
11,060 |
7,9216 |
6,6803 |
5,9984 |
5,5623 |
5,2574 |
5,0313 |
4,8566 |
4,7173 |
4,6034 |
4,4281 |
4,2468 |
4,0585 |
3,9614 |
3,8619 |
3,7600 |
3,6553 |
3,5473 |
3,4359 |
|
15 |
10,798 |
7,7008 |
6,4760 |
5,8029 |
5,3721 |
5,0708 |
4,8473 |
4,6743 |
4,5364 |
4,4236 |
4,2498 |
4,0698 |
3,8826 |
3,7859 |
3,6867 |
3,5850 |
3,4803 |
3,3722 |
3,2602 |
|
16 |
10,575 |
7,5138 |
6,3034 |
5,6378 |
5,2117 |
4,9134 |
4,6920 |
4,5207 |
4,3838 |
4,2719 |
4,0994 |
3,9205 |
3,7342 |
3,6378 |
3,5388 |
3,4372 |
3,3324 |
3,2240 |
3,1115 |
|
17 |
10,384 |
7,3536 |
6,1556 |
5,4967 |
5,0746 |
4,7789 |
4,5594 |
4,3893 |
4,2535 |
4,1423 |
3,9709 |
3,7929 |
3,6073 |
3,5112 |
3,4124 |
3,3107 |
3,2058 |
3,0971 |
2,9839 |
|
18 |
10,218 |
7,2148 |
6,0277 |
5,3746 |
4,9560 |
4,6627 |
4,4448 |
4,2759 |
4,1410 |
4,0305 |
3,8599 |
3,6827 |
3,4977 |
3,4017 |
3,3030 |
3,2014 |
3,0962 |
2,9871 |
2,8732 |
|
19 |
10,073 |
7,0935 |
5,9161 |
5,2681 |
4,8526 |
4,5614 |
4,3448 |
4,1770 |
4,0428 |
3,9329 |
3,7631 |
3,5866 |
3,4020 |
3,3062 |
3,2075 |
3,1058 |
3,0004 |
2,8908 |
2,7762 |
|
20 |
9,9439 |
6,9865 |
5,8177 |
5,1743 |
4,7616 |
4,4721 |
4,2569 |
4,0900 |
3,9564 |
3,8470 |
3,6779 |
3,5020 |
3,3178 |
3,2220 |
3,1234 |
3,0215 |
2,9159 |
2,8058 |
2,6904 |
|
21 |
9,8295 |
6,8914 |
5,7304 |
5,0911 |
4,6808 |
4,3931 |
4,1789 |
4,0128 |
3,8799 |
3,7709 |
3,6024 |
3,4270 |
3,2431 |
3,1474 |
3,0488 |
2,9467 |
2,8408 |
2,7302 |
2,6140 |
|
22 |
9,7271 |
6,8064 |
5,6524 |
5,0168 |
4,6088 |
4,3225 |
4,1094 |
3,9440 |
3,8116 |
3,7030 |
3,5350 |
3,3600 |
3,1764 |
3,0807 |
2,9821 |
2,8799 |
2,7736 |
2,6625 |
2,5455 |
|
23 |
9,6348 |
6,7300 |
5,5823 |
4,9500 |
4,5441 |
4,2591 |
4,0469 |
3,8822 |
3,7502 |
3,6420 |
3,4745 |
3,2999 |
3,1165 |
3,0208 |
2,9221 |
2,8198 |
2,7132 |
2,6016 |
2,4837 |
|
24 |
9,5513 |
6,6609 |
5,5190 |
4,8898 |
4,4857 |
4,2019 |
3,9905 |
3,8264 |
3,6949 |
3,5870 |
3,4199 |
3,2456 |
3,0624 |
2,9667 |
2,8679 |
2,7654 |
2,6585 |
2,5463 |
2,4276 |
|
25 |
9,4753 |
6,5982 |
5,4615 |
4,8351 |
4,4327 |
4,1500 |
3,9394 |
3,7758 |
3,6447 |
3,5370 |
3,3704 |
3,1963 |
3,0133 |
2,9176 |
2,8187 |
2,7160 |
2,6088 |
2,4960 |
2,3765 |
|
26 |
9,4059 |
6,5409 |
5,4091 |
4,7852 |
4,3844 |
4,1027 |
3,8928 |
3,7297 |
3,5989 |
3,4916 |
3,3252 |
3,1515 |
2,9685 |
2,8728 |
2,7738 |
2,6709 |
2,5633 |
2,4501 |
2,3297 |
|
27 |
9,3423 |
6,4885 |
5,3611 |
4,7396 |
4,3402 |
4,0594 |
3,8501 |
3,6875 |
3,5571 |
3,4499 |
3,2839 |
3,1104 |
2,9275 |
2,8318 |
2,7327 |
2,6296 |
2,5217 |
2,4079 |
2,2867 |
|
28 |
9,2838 |
6,4403 |
5,3170 |
4,6977 |
4,2996 |
4,0197 |
3,8110 |
3,6487 |
3,5186 |
3,4117 |
3,2460 |
3,0727 |
2,8899 |
2,7941 |
2,6949 |
2,5916 |
2,4834 |
2,3690 |
2,2469 |
|
29 |
9,2297 |
6,3958 |
5,2764 |
4,6591 |
4,2622 |
3,9830 |
3,7749 |
3,6130 |
3,4832 |
3,3765 |
3,2111 |
3,0379 |
2,8551 |
2,7594 |
2,6601 |
2,5565 |
2,4479 |
2,3331 |
2,2102 |
|
30 |
9,1797 |
6,3547 |
5,2388 |
4,6233 |
4,2276 |
3,9492 |
3,7416 |
3,5801 |
3,4505 |
3,3440 |
3,1787 |
3,0057 |
2,8230 |
2,7272 |
2,6278 |
2,5241 |
2,4151 |
2,2998 |
2,1760 |
|
40 |
8,8278 |
6,0664 |
4,9759 |
4,3738 |
3,9860 |
3,7129 |
3,5088 |
3,3498 |
3,2220 |
3,1167 |
2,9531 |
2,7811 |
2,5984 |
2,5020 |
2,4015 |
2,2958 |
2,1838 |
2,0635 |
1,9318 |
|
60 |
8,4946 |
5,7950 |
4,7290 |
4,1399 |
3,7600 |
3,4918 |
3,2911 |
3,1344 |
3,0083 |
2,9042 |
2,7419 |
2,5705 |
2,3872 |
2,2898 |
2,1874 |
2,0789 |
1,9622 |
1,8341 |
1,6885 |
|
120 |
8,1790 |
5,5393 |
4,4973 |
3,9207 |
3,5482 |
3,2849 |
3,0874 |
2,9330 |
2,8083 |
2,7052 |
2,5439 |
2,3727 |
2,1881 |
2,0890 |
1,9839 |
1,8709 |
1,7469 |
1,6055 |
1,4311 |
|
¥ |
7,8794 |
5,2983 |
4,2794 |
3,7151 |
3,3499 |
3,0913 |
2,8968 |
2,7444 |
2,6210 |
2,5188 |
2,3583 |
2,1868 |
1,9998 |
1,8983 |
1,7891 |
1,6691 |
1,5325 |
1,3637 |
1,0000 |
(Измененная редакция, Изм. №
1).
ТАБЛИЦА Г.6 - КВАНТИЛИ F-РАСПРЕДЕЛЕНИЯ
УРОВНЯ a = 0,9
|
v2 |
Квантили F-распределения уровня a = 0,9 для степени свободы v1 |
||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
12 |
15 |
20 |
24 |
30 |
40 |
60 |
120 |
¥ |
|
|
1 |
39,864 |
49,500 |
53,593 |
55,833 |
57,241 |
58,204 |
58,906 |
59,439 |
59,858 |
60,195 |
60,705 |
61,220 |
61,740 |
62,002 |
62,265 |
62,529 |
62,794 |
63,061 |
63,328 |
|
2 |
8,5263 |
9,0000 |
9,1618 |
9,2434 |
9,2926 |
9,3255 |
9,3491 |
9,3668 |
9,3805 |
9,3916 |
9,4081 |
9,4247 |
9,4413 |
9,4496 |
9,4579 |
9,4663 |
9,4746 |
9,4829 |
9,4913 |
|
3 |
5,5383 |
5,4624 |
5,3908 |
5,3427 |
5,3092 |
5,2847 |
5,2662 |
5,2517 |
5,2400 |
5,2304 |
5,2156 |
5,2003 |
5,1845 |
5,1764 |
5,1681 |
5,1597 |
5,1512 |
5,1425 |
5,1337 |
|
4 |
4,5448 |
4,3246 |
4,1908 |
4,1073 |
4,0506 |
4,0098 |
3,9790 |
3,9549 |
3,9357 |
3,9199 |
3,8955 |
3,S703 |
3,8443 |
3,8310 |
3,8174 |
3,8036 |
3,7896 |
3,7753 |
3,7607 |
|
5 |
4,0604 |
3,7797 |
3,6195 |
3,5202 |
3,4530 |
3,4045 |
3,3679 |
3,3393 |
3,3163 |
3,2974 |
3,2682 |
3,2380 |
3,2067 |
3,1905 |
3,1741 |
3,1573 |
3,1402 |
3,1228 |
3,1050 |
|
6 |
3,7760 |
3,4633 |
3,2888 |
3,1808 |
3,1075 |
3,0546 |
3,0145 |
2,9830 |
2,9577 |
2,9369 |
2,9047 |
2,8712 |
2,8363 |
2,8183 |
2,8000 |
2,7812 |
2,7620 |
2,7423 |
2,7222 |
|
7 |
3,5894 |
3,2574 |
3,0741 |
2,9605 |
2,8833 |
2,8274 |
2,7849 |
2,7516 |
2,7247 |
2,7025 |
2,6681 |
2,6322 |
2,5947 |
2,5753 |
2,5555 |
2,5351 |
2,5142 |
2,4928 |
2,4708 |
|
8 |
3,4579 |
3,1131 |
2,9238 |
2,8064 |
2,7265 |
2,6683 |
2,6241 |
2,5893 |
2,5612 |
2,5380 |
2,5020 |
2,4642 |
2,4246 |
2,4041 |
2,3830 |
2,3614 |
2,3391 |
2,3162 |
2,2926 |
|
9 |
3,3603 |
3,0065 |
2,8129 |
2,6927 |
2,6106 |
2,5509 |
2,5053 |
2,4694 |
2,4403 |
2,4163 |
2,3789 |
2,3396 |
2,2983 |
2,2768 |
2,2547 |
2,2320 |
2,2085 |
2,1843 |
2,1592 |
|
10 |
3,2850 |
2,9245 |
2,7277 |
2,6053 |
2,5216 |
2,4606 |
2,4140 |
2,3772 |
2,3473 |
2,3226 |
2,2841 |
2,2435 |
2,2007 |
2,1784 |
2,1554 |
2,1317 |
2,1072 |
2,0818 |
2,0554 |
|
11 |
3,2252 |
2,8595 |
2,6602 |
2,5362 |
2,4512 |
2,3891 |
2,3416 |
2,3040 |
2,2735 |
2,2482 |
2,2087 |
2,1671 |
2,1230 |
2,1000 |
2,0762 |
2,0516 |
2,0261 |
1,9997 |
1,9721 |
|
12 |
3,1765 |
2,8068 |
2,6055 |
2,4801 |
2,3940 |
2,3310 |
2,2828 |
2,2446 |
2,2135 |
2,1878 |
2,1474 |
2,1049 |
2,0597 |
2,0360 |
2,0115 |
1,9861 |
1,9597 |
1,9323 |
1,9036 |
|
13 |
3,1362 |
2,7632 |
2,5603 |
2,4337 |
2,3467 |
2,2830 |
2,2341 |
2,1953 |
2,1638 |
2,1376 |
2,0966 |
2,0532 |
2,0070 |
1,9827 |
1,9576 |
1,9315 |
1,9043 |
1,8759 |
1,8462 |
|
14 |
3,1022 |
2,7265 |
2,5222 |
2,3947 |
2,3069 |
2,2426 |
2,1931 |
2,1539 |
2,1220 |
2,0954 |
2,0537 |
2,0095 |
1,9625 |
1,9377 |
1,9119 |
1,8852 |
1,8572 |
1,8280 |
1,7973 |
|
15 |
3,0732 |
2,6952 |
2,4898 |
2,3614 |
2,2730 |
2,2081 |
2,1582 |
2,1185 |
2,0862 |
2,0593 |
2,0171 |
1,9722 |
1,9243 |
1,8990 |
1,8728 |
1,8454 |
1,8168 |
1,7867 |
1,7551 |
|
16 |
3,0481 |
2,6682 |
2,4618 |
2,3327 |
2,2438 |
2,1783 |
2,1280 |
2,0880 |
2,0553 |
2,0281 |
1,9854 |
1,9399 |
1,8913 |
1,8656 |
1,8388 |
1,8108 |
1,7816 |
1,7507 |
1,7182 |
|
17 |
3,0262 |
2,6446 |
2,4374 |
2,3077 |
2,2183 |
2,1524 |
2,1017 |
2,0613 |
2,0284 |
2,0009 |
1,9577 |
1,9117 |
1,8624 |
1,8362 |
1,8090 |
1,7805 |
1,7506 |
1,7191 |
1,6856 |
|
18 |
3,0070 |
2,6239 |
2,4160 |
2,2858 |
2,1958 |
2,1296 |
2,0785 |
2,0379 |
2,0047 |
1,9770 |
1,9333 |
1,8868 |
1,8368 |
1,8103 |
1,7827 |
1,7537 |
1,7232 |
1,6910 |
1,6567 |
|
19 |
2,9899 |
2,6056 |
2,3970 |
2,2663 |
2,1760 |
2,1094 |
2,0580 |
2,0171 |
1,9836 |
1,9557 |
1,9117 |
1,8647 |
1,8142 |
1,7873 |
1,7592 |
1,7298 |
1,6988 |
1,6659 |
1,6308 |
|
20 |
2,9747 |
2,5893 |
2,3801 |
2,2489 |
2,1582 |
2,0913 |
2,0397 |
1,9985 |
1,9649 |
1,9367 |
1,8924 |
1,8449 |
1,7938 |
1,7667 |
1,7382 |
1,7083 |
1,6768 |
1,6433 |
1,6074 |
|
21 |
2,9609 |
2,5746 |
2,3649 |
2,2333 |
2,1423 |
2,0751 |
2,0232 |
1,9819 |
1,9480 |
1,9197 |
1,8750 |
1,8272 |
1,7756 |
1,7481 |
1,7193 |
1,6890 |
1,6569 |
1,6228 |
1,5862 |
|
22 |
2,9486 |
2,5613 |
2,3512 |
2,2193 |
2,1279 |
2,0605 |
2,0084 |
1,9668 |
1,9327 |
1,9043 |
1,8593 |
1,8111 |
1,7590 |
1,7312 |
1,7021 |
1,6714 |
1,6389 |
1,6042 |
1,5668 |
|
23 |
2,9374 |
2,5493 |
2,3387 |
2,2065 |
2,1149 |
2,0472 |
1,9949 |
1,9531 |
1,9189 |
1,8903 |
1,8450 |
1,7964 |
1,7439 |
1,7159 |
1,6864 |
1,6554 |
1,6224 |
1,5871 |
1,5490 |
|
24 |
2,9271 |
2,5383 |
2,3274 |
2,1949 |
2,1030 |
2,0351 |
1,9826 |
1,9407 |
1,9063 |
1,3775 |
1,8319 |
1,7831 |
1,7302 |
1,7019 |
1,6721 |
1,6407 |
1,6073 |
1,5715 |
1,5327 |
|
25 |
2,9177 |
2,5283 |
2,3170 |
2,1843 |
2,0922 |
2,0241 |
1,9714 |
1,9292 |
1,8947 |
1,8658 |
1,8200 |
1,7708 |
1,7175 |
1,6890 |
1,6589 |
1,6272 |
1,5934 |
1,5570 |
1,5176 |
|
26 |
2,9091 |
2,5191 |
2,3075 |
2,1745 |
2,0822 |
2,0139 |
1,9610 |
1,9188 |
1,8841 |
1,8550 |
1,8090 |
1,7596 |
1,7059 |
1,6771 |
1,6468 |
1,6147 |
1,5805 |
1,5437 |
1,5036 |
|
27 |
2,9012 |
2,5106 |
2,2987 |
2,1655 |
2,0730 |
2,0045 |
1,9515 |
1,9091 |
1,8743 |
1,8451 |
1,7989 |
1,7492 |
1,6951 |
1,6662 |
1,6356 |
1,6032 |
1,5686 |
1,5313 |
1,4906 |
|
28 |
2,8939 |
2,5028 |
2,2906 |
2,1571 |
2,0645 |
1,9959 |
1,9427 |
1,9001 |
1,8652 |
1,8359 |
1,7895 |
1,7395 |
1,6852 |
1,6560 |
1,6252 |
1,5925 |
1,5575 |
1,5198 |
1,4784 |
|
29 |
2,8871 |
2,4955 |
2,2831 |
2,1494 |
2,0566 |
1,9878 |
1,9345 |
1,8918 |
1,8568 |
1,8274 |
1,7808 |
1,7306 |
1,6759 |
1,6465 |
1,6155 |
1,5825 |
1,5472 |
1,5090 |
1,4670 |
|
30 |
2,8807 |
2,4887 |
2,2761 |
2,1422 |
2,0492 |
1,9803 |
1,9269 |
1,8841 |
1,8490 |
1,8195 |
1,7727 |
1,7223 |
1,6673 |
1,6377 |
1,6065 |
1,5732 |
1,5376 |
1,4989 |
1,4564 |
|
40 |
2,8354 |
2,4404 |
2,2261 |
2,0909 |
1,9968 |
1,9269 |
1,8725 |
1,8289 |
1,7929 |
1,7627 |
1,7146 |
1,6624 |
1,6052 |
1,5741 |
1,5411 |
1,5056 |
1,4672 |
1,4248 |
1,3769 |
|
60 |
2,7914 |
2,3933 |
2,1774 |
2,0410 |
1,9457 |
1,8747 |
1,8194 |
1,7748 |
1,7380 |
1,7070 |
1,6574 |
1,6034 |
1,5435 |
1,5107 |
1,4755 |
1,4373 |
1,3952 |
1,3476 |
1,2915 |
|
120 |
2,7478 |
2,3473 |
2,1300 |
1,9923 |
1,8959 |
1,8238 |
1,7675 |
1,7220 |
1,6843 |
1,6524 |
1,6012 |
1,5450 |
1,4821 |
1,4472 |
1,4094 |
1,3676 |
1,3203 |
1,2646 |
1,1926 |
|
¥ |
2,7055 |
2,3026 |
2,0838 |
1,9449 |
1,8473 |
1,7741 |
1,7167 |
1,6702 |
1,6315 |
1,5987 |
1,5458 |
1,4871 |
1,4206 |
1,3832 |
1,3419 |
1,2951 |
1,2400 |
1,1686 |
1,0000 |
(Измененная редакция, Изм. №
1).
ТАБЛИЦА Г.7- КВАНТИЛИ F-РАСПРЕДЕЛЕНИЯ
УРОВНЯ a = 0,95
|
v2 |
Квантили F-распределения уровня a = 0,95 для степени свободы v1 |
||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
15 |
20 |
30 |
40 |
60 |
120 |
¥ |
|
|
1 |
161,45 |
199,50 |
215,71 |
224,58 |
230,16 |
233,99 |
236,77 |
238,88 |
240,54 |
241,88 |
243,91 |
245,95 |
248,01 |
249,05 |
250,09 |
251,14 |
252,20 |
253,25 |
254,32 |
|
2 |
18,513 |
19,000 |
19,164 |
19,247 |
19,296 |
19,330 |
19,353 |
19,371 |
19,385 |
19,396 |
19,413 |
19,429 |
19,446 |
19,454 |
19,462 |
19,471 |
19,479 |
19,487 |
19,496 |
|
3 |
10,128 |
9,5521 |
9,2766 |
9,1172 |
9,0135 |
8,9406 |
8,8868 |
8,8452 |
8,8123 |
8,7855 |
8,7446 |
8,7029 |
8,6602 |
8,6385 |
8,6166 |
8,5944 |
8,5720 |
8,5494 |
8,5265 |
|
4 |
7,7086 |
6,9443 |
6,5914 |
6,3883 |
6,2560 |
6,1631 |
6,0942 |
6,0410 |
5,9988 |
5,9644 |
5,9117 |
5,8578 |
5,8025 |
5,7744 |
5,7459 |
5,7170 |
5,6878 |
5,6581 |
5,6281 |
|
5 |
6,6079 |
5,7861 |
5,4095 |
5,1922 |
5,0503 |
4,9503 |
4,8759 |
4,8183 |
4,7725 |
4,7351 |
4,6777 |
4,6188 |
4,5581 |
4,5272 |
4,4957 |
4,4638 |
4,4314 |
4,3984 |
4,3650 |
|
6 |
5,9874 |
5,1433 |
4,7571 |
4,5337 |
4,3874 |
4,2839 |
4,2066 |
4,1468 |
4,0990 |
4,0600 |
3,9999 |
3,9381 |
3,8742 |
3,8415 |
3,8082 |
3,7743 |
3,7398 |
3,7047 |
3,6688 |
|
7 |
5,5914 |
4,7374 |
4,3468 |
4,1203 |
3,9715 |
3,8660 |
3,7870 |
3,7257 |
3,6767 |
3,6365 |
3,5747 |
3,5108 |
3,4445 |
3,4105 |
3,3758 |
3,3404 |
3,3043 |
3,2674 |
3,2298 |
|
8 |
5,3177 |
4,4590 |
4,0662 |
3,8378 |
3,6875 |
3,5806 |
3,5005 |
3,4381 |
3,3881 |
3,3472 |
3,2840 |
3,2184 |
3,1503 |
3,1152 |
3,0794 |
3,0428 |
3,0053 |
2,9669 |
2,9276 |
|
9 |
5,1174 |
4,2565 |
3,8626 |
3,6331 |
3,4817 |
3,3738 |
3,2927 |
3,2296 |
3,1789 |
3,1373 |
3,0729 |
3,0061 |
2,9365 |
2,9005 |
2,8637 |
2,8259 |
2,7872 |
2,7475 |
2,7067 |
|
10 |
4,9646 |
4,1028 |
3,7083 |
3,4780 |
3,3258 |
3,2172 |
3,1355 |
3,0717 |
3,0204 |
2,9782 |
2,9130 |
2,8450 |
2,7740 |
2,7372 |
2,6996 |
2,6609 |
2,6211 |
2,5801 |
2,5379 |
|
11 |
4,8443 |
3,9823 |
3,5874 |
3,3567 |
3,2039 |
3,0946 |
3,0123 |
2,9480 |
2,8962 |
2,8536 |
2,7876 |
2,7186 |
2,6464 |
2,6090 |
2,5705 |
2,5309 |
2,4901 |
2,4480 |
2,4045 |
|
12 |
4,7472 |
3,8853 |
3,4903 |
3,2592 |
3,1059 |
2,9961 |
2,9134 |
2,8486 |
2,7964 |
2,7534 |
2,6866 |
2,6169 |
2,5436 |
2,5055 |
2,4663 |
2,4259 |
2,3842 |
2,3410 |
2,2962 |
|
13 |
4,6672 |
3,8056 |
3,4105 |
3,1791 |
3,0254 |
2,9153 |
2,8321 |
2,7669 |
2,7144 |
2,6710 |
2,6037 |
2,5331 |
2,4589 |
2,4202 |
2,3803 |
2,3392 |
2,2966 |
2,2524 |
2,2064 |
|
14 |
4,6001 |
3,7389 |
3,3439 |
3,1122 |
2,9582 |
2,8477 |
2,7642 |
2,6987 |
2,6458 |
2,6021 |
2,5342 |
2,4630 |
2,3879 |
2,3487 |
2,3082 |
2,2664 |
2,2230 |
2,1778 |
2,1307 |
|
15 |
4,5431 |
3,6823 |
3,2874 |
3,0556 |
2,9013 |
2,7905 |
2,7066 |
2,6408 |
2,5876 |
2,5437 |
2,4753 |
2,4035 |
2,3275 |
2,2878 |
2,2468 |
2,2043 |
2,1601 |
2,1141 |
2,0658 |
|
16 |
4,4940 |
3,6337 |
3,2389 |
3,0069 |
2,8524 |
2,7413 |
2,6572 |
2,5911 |
2,5377 |
2,4935 |
2,4247 |
2,3522 |
2,2756 |
2,2354 |
2,1938 |
2,1507 |
2,1058 |
2,0589 |
2,0096 |
|
17 |
4,4513 |
3,5915 |
3,1968 |
2,9647 |
2,8100 |
2,6987 |
2,6143 |
2,5480 |
2,4943 |
2,4499 |
2,3807 |
2,3077 |
2,2304 |
2,1898 |
2,1477 |
2,1040 |
2,0584 |
2,0107 |
1,9604 |
|
18 |
4,4139 |
3,5546 |
3,1599 |
2,9277 |
2,7729 |
2,6613 |
2,5767 |
2,5102 |
2,4563 |
2,4117 |
2,3421 |
2,2686 |
2,1906 |
2,1497 |
2,1071 |
2,0629 |
2,0166 |
1,9681 |
1,9168 |
|
19 |
4,3808 |
3,5219 |
3,1274 |
2,8951 |
2,7401 |
2,6283 |
2,5435 |
2,4768 |
2,4227 |
2,3779 |
2,3080 |
2,2341 |
2,1555 |
2,1141 |
2,0712 |
2,0264 |
1,9796 |
1,9302 |
1,8780 |
|
20 |
4,3513 |
3,4928 |
3,0984 |
2,8661 |
2,7109 |
2,5990 |
2,5140 |
2,4471 |
2,3928 |
2,3479 |
2,2776 |
2,2033 |
2,1242 |
2,0825 |
2,0391 |
1,9938 |
1,9464 |
1,8963 |
1,8432 |
|
21 |
4,3248 |
3,4668 |
3,0725 |
2,8401 |
2,6848 |
2,5727 |
2,4876 |
2,4205 |
2,3661 |
2,3210 |
2,2504 |
2,1757 |
2,0960 |
2,0540 |
2,0102 |
1,9645 |
1,9165 |
1,8657 |
1,8117 |
|
22 |
4,3009 |
3,4434 |
3,0491 |
2,8167 |
2,6613 |
2,5491 |
2,4638 |
2,3965 |
2,3419 |
2,2967 |
2,2258 |
2,1508 |
2,0707 |
2,0283 |
1,9842 |
1,9380 |
1,8895 |
1,8380 |
1,7831 |
|
23 |
4,2793 |
3,4221 |
3,0280 |
2,7955 |
2,6400 |
2,5277 |
2,4422 |
2,3748 |
2,3201 |
2,2747 |
2,2036 |
2,1282 |
2,0476 |
2,0050 |
1,9605 |
1,9139 |
1,8649 |
1,8128 |
1,7570 |
|
24 |
4,2597 |
3,4028 |
3,0088 |
2,7763 |
2,6207 |
2,5082 |
2,4226 |
2,3551 |
2,3002 |
2,2547 |
2,1834 |
2,1077 |
2,0267 |
1,9838 |
1,9390 |
1,8920 |
1,8424 |
1,7897 |
1,7331 |
|
25 |
4,2417 |
3,3852 |
2,9912 |
2,7587 |
2,6030 |
2,4904 |
2,4047 |
2,3371 |
2,2821 |
2,2365 |
2,1649 |
2,0889 |
2,0075 |
1,9643 |
1,9192 |
1,8718 |
1,8217 |
1,7684 |
1,7110 |
|
26 |
4,2252 |
3,3690 |
2,9751 |
2,7426 |
2,5868 |
2,4741 |
2,3883 |
2,3205 |
2,2655 |
2,2197 |
2,1479 |
2,0716 |
1,9898 |
1,9464 |
1,9010 |
1,8533 |
1,8027 |
1,7488 |
1,6906 |
|
27 |
4,2100 |
3,3541 |
2,9604 |
2,7278 |
2,5719 |
2,4591 |
2,3732 |
2,3053 |
2,2501 |
2,2043 |
2,1323 |
2,0558 |
1,9736 |
1,9299 |
1,8842 |
1,8361 |
1,7851 |
1,7307 |
1,6717 |
|
28 |
4,1960 |
3,3404 |
2,9467 |
2,7141 |
2,5581 |
2,4453 |
2,3593 |
2,2913 |
2,2360 |
2,1900 |
2,1179 |
2,0411 |
1,9586 |
1,9147 |
1,8687 |
1,8203 |
1,7689 |
1,7138 |
1,6541 |
|
29 |
4,1830 |
3,3277 |
2,9340 |
2,7014 |
2,5454 |
2,4324 |
2,3463 |
2,2782 |
2,2229 |
2,1768 |
2,1045 |
2,0275 |
1,9446 |
1,9005 |
1,8543 |
1,8055 |
1,7537 |
1,6981 |
1,6377 |
|
30 |
4,1709 |
3,3158 |
2,9223 |
2,6896 |
2,5336 |
2,4205 |
2,3343 |
2,2662 |
2,2107 |
2,1646 |
2,0921 |
2,0148 |
1,9317 |
1,8874 |
1,8409 |
1,7918 |
1,7396 |
1,6835 |
1,6223 |
|
40 |
4,0848 |
3,2317 |
2,8387 |
2,6060 |
2,4459 |
2,3359 |
2,2400 |
2,1802 |
2,1240 |
2,0772 |
2,0035 |
1,9245 |
1,8389 |
1,7929 |
1,7444 |
1,6928 |
1,6373 |
1,5766 |
1,5089 |
|
60 |
4,0012 |
3,1504 |
2,7581 |
2,5252 |
2,3683 |
2,2540 |
2,1665 |
2,0970 |
2,0401 |
1,9926 |
1,9174 |
1,8364 |
1,7480 |
1,7001 |
1,6491 |
1,5943 |
1,5343 |
1,4673 |
1,3893 |
|
120 |
3,9201 |
3,0718 |
2,6802 |
2,4472 |
2,2900 |
2,1750 |
2,0867 |
2,0164 |
1,9588 |
1,9105 |
1,8337 |
1,7505 |
1,6587 |
1,6084 |
1,5543 |
1,4952 |
1,4290 |
1,3519 |
1,2539 |
|
¥ |
3,8415 |
2,9957 |
2,6049 |
2,3719 |
2,2141 |
2,0986 |
2,0096 |
1,9384 |
1,8799 |
1,8307 |
1,7522 |
1,6664 |
1,5705 |
1,5173 |
1,4591 |
1,3940 |
1,3180 |
1,2214 |
1,0000 |
(Измененная редакция, Изм. №
1).
ТАБЛИЦА Г.8 - КВАНТИЛИ F-РАСПРЕДЕЛЕНИЯ УРОВНЯ a = 0,975
|
v2 |
Квантили F-распределения уровня a = 0,975 для степени свободы v1 |
||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
15 |
20 |
24 |
30 |
40 |
60 |
120 |
¥ |
|
|
1 |
647,79 |
799,50 |
864,16 |
899,58 |
921,85 |
937,11 |
948,22 |
956,66 |
963,28 |
968,63 |
976,71 |
984,87 |
993,10 |
997,25 |
1001,4 |
1005,6 |
1009,8 |
1014,0 |
1018,3 |
|
2 |
38,506 |
39,000 |
39,165 |
39,248 |
39,298 |
39,331 |
39,355 |
39,373 |
39,387 |
39,398 |
39,415 |
39,431 |
39,448 |
39,456 |
39,465 |
39,473 |
39,481 |
39,490 |
39,498 |
|
3 |
17,443 |
16,044 |
15,439 |
15,101 |
14,885 |
14,735 |
14,624 |
14,540 |
14,473 |
14,419 |
14,337 |
14,253 |
14,167 |
14,124 |
14,081 |
14,037 |
13,992 |
13,947 |
13,902 |
|
4 |
12,218 |
10,649 |
9,9792 |
9,6045 |
9,3645 |
9,1973 |
9,0741 |
8,9796 |
8,9047 |
8,8439 |
8,7512 |
8,6565 |
8,5599 |
8,5109 |
8,4613 |
8,4111 |
8,3604 |
8,3092 |
8,2573 |
|
5 |
10,007 |
8,4336 |
7,7636 |
7,3879 |
7,1464 |
6,9777 |
6,8531 |
6,7572 |
6,6810 |
6,6192 |
6,5246 |
6,4227 |
6,3285 |
6,2780 |
6,2269 |
6,1751 |
6,1225 |
6,0693 |
6,0153 |
|
6 |
8,8131 |
7,2598 |
6,5988 |
6,2272 |
5,9876 |
5,8197 |
5,6955 |
5,5996 |
5,5234 |
5,4613 |
5,3662 |
5,2687 |
5,1684 |
5,1172 |
5,0652 |
5,0125 |
4,9589 |
4,9045 |
4,8491 |
|
7 |
8,0727 |
6,5415 |
5,8898 |
5,5226 |
5,2852 |
5,1186 |
4,9949 |
4,8994 |
4,8232 |
4,7611 |
4,6658 |
4,5678 |
4,4667 |
4,4150 |
4,3624 |
4,3089 |
4,2544 |
4,1989 |
4,1423 |
|
8 |
7,5709 |
6,0595 |
5,4160 |
5,0526 |
4,8173 |
4,6517 |
4,5286 |
4,4332 |
4,3572 |
4,2951 |
4,1997 |
4,1012 |
3,9995 |
3,9472 |
3,8940 |
3,8398 |
3,7844 |
3,7279 |
3,6702 |
|
9 |
7,2093 |
5,7147 |
5,0781 |
4,7181 |
4,4844 |
4,3197 |
4,1971 |
4,1020 |
4,0260 |
3,9639 |
3,8682 |
3,7694 |
3,6669 |
3,6142 |
3,5604 |
3,5055 |
3,4493 |
3,3918 |
3,3329 |
|
10 |
6,9367 |
5,4564 |
4,8256 |
4,4683 |
4,2361 |
4,0721 |
3,9498 |
3,8549 |
3,7790 |
3,7168 |
3,6209 |
3,5217 |
3,4186 |
3,3654 |
3,3110 |
3,2554 |
3,1984 |
3,1399 |
3,0798 |
|
11 |
6,7241 |
5,2559 |
4,6300 |
4,2751 |
4,0440 |
3,8807 |
3,7586 |
3,6638 |
3,5879 |
3,5257 |
3,4296 |
3,3299 |
3,2261 |
3,1725 |
3,1176 |
3,0613 |
3,0035 |
2,9441 |
2,8828 |
|
12 |
6,5538 |
5,0959 |
4,4742 |
4,1212 |
3,8911 |
3,7283 |
3,6065 |
3,5118 |
3,4358 |
3,3736 |
3,2773 |
3,1772 |
3,0728 |
3,0187 |
2,9633 |
2,9063 |
2,8478 |
2,7874 |
2,7249 |
|
13 |
6,4143 |
4,9653 |
4,3472 |
3,9959 |
3,7667 |
3,6043 |
3,4827 |
,3,3880 |
3,3120 |
3,2497 |
3,1532 |
3,0527 |
2,9477 |
2,8932 |
2,8373 |
2,7797 |
2,7204 |
2,6590 |
2,5955 |
|
14 |
6,2979 |
4,8567 |
4,2417 |
3,8919 |
3,6634 |
3,5014 |
3,3799 |
3,2853 |
3,2093 |
3,1469 |
3,0501 |
2,9493 |
2,8437 |
2,7888 |
2,7324 |
2,6742 |
2,6142 |
2,5519 |
2,4872 |
|
15 |
6,1995 |
4,7650 |
4,1528 |
3,8043 |
3,5764 |
3,4147 |
3,2934 |
3,1987 |
3,1227 |
3,0602 |
2,9633 |
2,8621 |
2,7551 |
2,7006 |
2,6437 |
2,5850 |
2,5242 |
2,4611 |
2,3953 |
|
16 |
6,1151 |
4,6867 |
4,0768 |
3,7294 |
3,5021 |
3,3406 |
3,2194 |
3,1248 |
3,0488 |
2,9862 |
2,8890 |
2,7875 |
2,6808 |
2,6252 |
2,5678 |
2,5085 |
2,4471 |
2,3831 |
2,3163 |
|
17 |
6,0420 |
4,6189 |
4,0112 |
3,6648 |
3,4379 |
3,2767 |
3,1556 |
3,0610 |
2,9849 |
2,9222 |
2,8249 |
2,7230 |
2,6158 |
2,5598 |
2,5021 |
2,4422 |
2,3801 |
2,3153 |
2,2474 |
|
18 |
5,9781 |
4,5597 |
3,9539 |
3,6083 |
3,3820 |
3,2209 |
3,0999 |
3,0053 |
2,9291 |
2,S664 |
2,7689 |
2,6667 |
2,5590 |
2,5027 |
2,4445 |
2,3842 |
2,3214 |
2,2558 |
2,1869 |
|
19 |
5,9216 |
4,5075 |
3,9034 |
3,5587 |
3,3327 |
3,1718 |
3,0509 |
2,9563 |
2,8800 |
2,8173 |
2,7196 |
2,6171 |
2,5089 |
2,4523 |
2,3937 |
2,3329 |
2,2695 |
2,2032 |
2,1333 |
|
20 |
5,8715 |
4,4613 |
3,8587 |
3,5147 |
3,2891 |
3,1283 |
3,0074 |
2,9128 |
2,8365 |
2,7737 |
2,6758 |
2,5731 |
2,4645 |
2,4076 |
2,3486 |
2,2873 |
2,2234 |
2,1562 |
2,0853 |
|
21 |
5,8266 |
4,4199 |
3,8188 |
3,4754 |
3,2501 |
3,0895 |
2,9686 |
2,8740 |
2,7977 |
2,7348 |
2,6368 |
2,5338 |
2,4247 |
2,3675 |
2,3082 |
2,2465 |
2,1819 |
2,1141 |
2,0422 |
|
22 |
5,7863 |
4,3828 |
3,7829 |
3,4401 |
3,2151 |
3,0546 |
2,9338 |
2,8392 |
2,7628 |
2,6998 |
2,6017 |
2,4984 |
2,3890 |
2,3315 |
2,2718 |
2,2097 |
2,1446 |
2,0760 |
2,0032 |
|
23 |
5,7498 |
4,3492 |
3,7505 |
3,4083 |
3,1835 |
3,0232 |
2,9024 |
2,8077 |
2,7313 |
2,6682 |
2,5699 |
,2,4665 |
2,3567 |
2,2989 |
2,2389 |
2,1763 |
2,1107 |
2,0415 |
1,9677 |
|
24 |
5,7167 |
4,3187 |
3,7211 |
3,3794 |
3,1548 |
3,9946 |
2,8738 |
2,7791 |
2,7027 |
2,6396 |
2,5412 |
2,4374 |
2,3273 |
2,2693 |
2,2090 |
2,1460 |
2,0799 |
2,0099 |
1,9353 |
|
25 |
5,6864 |
4,2909 |
3,6943 |
3,3530 |
3,1287 |
2,9685 |
2,8478 |
2,7531 |
2,6766 |
2,6135 |
2,5149 |
2,4110 |
2,3005 |
2,2422 |
2,1816 |
2,1183 |
2,0517 |
1,9811 |
1,9055 |
|
26 |
5,6586 |
4,2655 |
3,6697 |
3,3289 |
3,1048 |
2,9447 |
2,8240 |
2,7293 |
2,6528 |
2,5895 |
2,4909 |
2,3867 |
2,2759 |
2,2174 |
2,1565 |
2,0928 |
2,0257 |
1,9545 |
1,8781 |
|
27 |
5,6331 |
4,2421 |
3,6472 |
3,3067 |
3,0828 |
2,9228 |
2,8021 |
2,7074 |
2,6309 |
2,5676 |
2,4688 |
2,3644 |
2,2533 |
2,1946 |
2,1334 |
2,0693 |
2,0018 |
1,9299 |
1,8527 |
|
28 |
5,6096 |
4,2205 |
3,6264 |
3,2863 |
3,0625 |
2,9027 |
2,7820 |
2,6872 |
2,6106 |
2,5473 |
2,4484 |
2,3438 |
2,2324 |
2,1735 |
2,1121 |
2,0477 |
1,9796 |
1,9072 |
1,8291 |
|
29 |
5,5878 |
4,2006 |
3,6072 |
3,2674 |
3,0438 |
2,8840 |
2,7633 |
2,6686 |
2,5919 |
2,5286 |
2,4295 |
2,3248 |
2,2131 |
2,1540 |
2,0923 |
2,0276 |
1,9591 |
1,8861 |
1,8072 |
|
30 |
5,5675 |
4,1821 |
3,5894 |
3,2499 |
3,0265 |
2,8667 |
2,7460 |
2,6513 |
2,5746 |
2,5112 |
2,4120 |
2,3072 |
2,1952 |
2,1359 |
2,0739 |
2,0089 |
1,9400 |
1,8664 |
1,7867 |
|
40 |
5,4239 |
4,0510 |
3,4633 |
3,1261 |
2,9037 |
2,7444 |
2,6238 |
2,5289 |
2,4519 |
2,3382 |
2,2882 |
2,1819 |
2,0677 |
2,0069 |
1,9429 |
1,8752 |
1,8028 |
1,7242 |
1,6371 |
|
60 |
5,2857 |
3,9253 |
3,3425 |
3,0077 |
2,7863 |
2,6274 |
2,5068 |
2,4117 |
2,3344 |
2,2702 |
2,1692 |
2,0613 |
1,9445 |
1,8817 |
1,8152 |
1,7440 |
1,6668 |
1,5810 |
1,4822 |
|
120 |
5,1524 |
3,8046 |
3,2270 |
2,8943 |
2,6740 |
2,5154 |
2,3948 |
2,2994 |
2,2217 |
2,1570 |
2,0548 |
1,9450 |
1,8249 |
1,7597 |
1,6899 |
1,6141 |
1,5299 |
1,4327 |
1,3104 |
|
¥ |
5,0239 |
3,6889 |
3,1161 |
2,7858 |
2,5665 |
2,4082 |
2,2875 |
2,1918 |
2,1136 |
2,0483 |
1,9447 |
1,3326 |
1,7085 |
1,6402 |
1,5660 |
1,4835 |
1,3883 |
1,2684 |
1,0000 |
(Измененная редакция, Изм. №
1).
ТАБЛИЦА Г.9 - КВАНТИЛИ F-РАСПРЕДЕЛЕНИЯ УРОВНЯ a = 0,99
|
v2 |
Квантили F-распределения уровня a = 0,99 для степени свободы v1 |
||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
15 |
20 |
30 |
40 |
60 |
120 |
¥ |
|
|
1 |
4052,2 |
4999,5 |
5403,3 |
5624,6 |
5763,7 |
5859,0 |
5928,3 |
5981,1 |
6022,5 |
6055,8 |
6106,3 |
6157,3 |
6208,7 |
6234,6 |
6260,7 |
6286,8 |
6313,0 |
6339,4 |
6366,0 |
|
2 |
98,503 |
99,000 |
99,166 |
99,249 |
99,299 |
99,332 |
99,356 |
99,374 |
99,388 |
99,399 |
99,416 |
99,432 |
99,449 |
99,458 |
99,466 |
99,474 |
99,483 |
99,491 |
99,499 |
|
3 |
34,116 |
30,817 |
29,457 |
28,710 |
28,237 |
27,911 |
27,672 |
27,489 |
27,345 |
27,229 |
27,052 |
26,872 |
26,690 |
26,598 |
26,505 |
26,411 |
26,316 |
26,221 |
26,125 |
|
4 |
21,198 |
18,000 |
16,694 |
15,977 |
15,522 |
15,207 |
14,976 |
14,799 |
14,659 |
14,546 |
14,374 |
14,198 |
14,020 |
13,929 |
13,838 |
13,745 |
13,652 |
13,558 |
13,463 |
|
5 |
16,258 |
13,274 |
12,060 |
11,392 |
10,967 |
10,672 |
10,456 |
10,289 |
10,158 |
10,051 |
9,8883 |
9,7222 |
9,5527 |
9,4665 |
9,3793 |
9,2912 |
9,2020 |
9,1118 |
9,0204 |
|
6 |
13,745 |
10,925 |
9,7795 |
9,1483 |
8,7459 |
8,4661 |
8,2600 |
8,1016 |
7,9761 |
7,8741 |
7,7183 |
7,5590 |
7,3958 |
7,3127 |
7,2285 |
7,1432 |
7,0568 |
6,9690 |
6,8861 |
|
7 |
12,246 |
9,5466 |
8,4513 |
7,8467 |
7,4604 |
7,1914 |
6,9928 |
6,8401 |
6,7188 |
6,6201 |
6,4691 |
6,3143 |
6,1554 |
6,0743 |
5,9921 |
5,9084 |
5,8236 |
5,7372 |
5,6495 |
|
8 |
11,259 |
8,6491 |
7,5910 |
7,0060 |
6,6318 |
6,3707 |
6,1776 |
6,0289 |
5,9106 |
5,8143 |
5,6668 |
5,5151 |
5,3591 |
5,2793 |
5,1981 |
5,1156 |
5,0316 |
4,9460 |
4,8588 |
|
9 |
10,561 |
8,0215 |
6,9919 |
6,4221 |
6,0569 |
5,8018 |
5,6129 |
5,4671 |
5,3511 |
5,2565 |
5,1114 |
4,9621 |
4,8080 |
4,7290 |
4,6486 |
4,5667 |
4,4831 |
4,3978 |
4,3105 |
|
10 |
10,044 |
7,5594 |
6,5523 |
5,9943 |
5,6363 |
5,3858 |
5,2001 |
5,0567 |
4,9424 |
4,8492 |
4,7059 |
4,5582 |
4,4054 |
4,3269 |
4,2469 |
4,1653 |
4,0819 |
3,9965 |
3,9090 |
|
11 |
9,6460 |
7,2057 |
6,2167 |
5,6683 |
5,3160 |
5,0692 |
4,8861 |
4,7445 |
4,6315 |
4,5393 |
4,3974 |
4,2509 |
4,0990 |
4,0209 |
3,9411 |
3,8596 |
3,7761 |
3,6904 |
3,6025 |
|
12 |
9,3302 |
6,9266 |
5,9526 |
5,4119 |
5,0643 |
4,8206 |
4,6395 |
4,4994 |
4,3875 |
4,2961 |
4,1553 |
4,0096 |
3,8584 |
3,7805 |
3,7008 |
3,6192 |
3,5355 |
3,4494 |
3,3608 |
|
13 |
9,0738 |
6,7010 |
5,7394 |
5,2053 |
4,8616 |
4,6204 |
4,4410 |
4,3021 |
4,1911 |
4,1003 |
3,9603 |
3,8154 |
3,6646 |
3,5868 |
3,5070 |
3,4253 |
3,3413 |
3,2548 |
3,1654 |
|
14 |
8,8616 |
6,5149 |
5,5639 |
5,0354 |
4,6950 |
4,4558 |
4,2779 |
4,1399 |
4,0297 |
3,9394 |
3,8001 |
3,6557 |
3,5052 |
3,4274 |
3,3476 |
3,2656 |
3,1813 |
3,0942 |
3,0040 |
|
15 |
8,6831 |
6,3589 |
5,4170 |
4,8932 |
4,5556 |
4,3183 |
4,1415 |
4,0045 |
3,8948 |
3,8049 |
3,6662 |
3,5222 |
3,3719 |
3,2940 |
3,2141 |
3,1319 |
3,0471 |
3,2995 |
2,8684 |
|
16 |
8,5310 |
6,2262 |
5,2922 |
4,7726 |
4,4374 |
4,2016 |
4,0259 |
3,8896 |
3,7804 |
3,6909 |
3,5527 |
3,4089 |
3,2588 |
3,1808 |
3,1007 |
3,0182 |
2,9330 |
2,8447 |
2,7528 |
|
17 |
8,3997 |
6,1121 |
5,1850 |
4,6690 |
4,3359 |
4,1015 |
3,9267 |
3,7910 |
3,6822 |
3,5931 |
3,4552 |
3,3117 |
3,1615 |
3,0835 |
3,0032 |
2,9205 |
2,8348 |
2,7459 |
2,6530 |
|
18 |
8,2854 |
6,0129 |
5,0919 |
4,5790 |
4,2479 |
4,0146 |
3,8406 |
3,7054 |
3,5971 |
3,5082 |
3,3706 |
3,2273 |
3,0771 |
2,9990 |
2,9185 |
2,8354 |
2,7493 |
2,6597 |
2,5660 |
|
19 |
8,1850 |
5,9259 |
5,0103 |
4,5003 |
4,1708 |
3,9386 |
3,7653 |
3,6305 |
3,5225 |
3,4338 |
3,2965 |
3,1533 |
3,0031 |
2,9249 |
2,8442 |
2,7608 |
2,6742 |
2,5839 |
2,4893 |
|
20 |
8,0960 |
5,8489 |
4,9382 |
4,4307 |
4,1027 |
3,8714 |
3,6987 |
3,5644 |
3,4567 |
3,3682 |
3,2311 |
3,0880 |
2,9377 |
2,8594 |
2,7785 |
2,6947 |
2,6077 |
2,5168 |
2,4212 |
|
21 |
8,0166 |
5,7804 |
4,8740 |
4,3688 |
4,0421 |
3,8117 |
3,6396 |
3,5056 |
3,3981 |
3,3098 |
3,1729 |
3,0299 |
2,8796 |
2,8011 |
2,7200 |
2,6359 |
2,5484 |
2,4568 |
2,3603 |
|
22 |
7,9454 |
5,7190 |
4,8166 |
4,3134 |
3,9880 |
3,7583 |
3,5867 |
3,4530 |
3,3458 |
3,2576 |
3,1209 |
2,9780 |
2,8274 |
2,7488 |
2,6675 |
2,5831 |
2,4951 |
2,4029 |
2,3055 |
|
23 |
7,8811 |
5,6637 |
4,7649 |
4,2635 |
3,9392 |
3,7102 |
3,5390 |
3,4057 |
3,2986 |
3,2106 |
3,0740 |
2,9311 |
2,7805 |
2,7017 |
2,6202 |
2,5355 |
2,4471 |
2,3542 |
2,2559 |
|
24 |
7,8229 |
5,6136 |
4,7181 |
4,2184 |
3,8951 |
3,6667 |
3,4959 |
3,3629 |
3,2560 |
3,1681 |
3,0316 |
2,8887 |
2,7380 |
2,6591 |
2,5773 |
2,4923 |
2,4035 |
2,3099 |
2,2107 |
|
25 |
7,7698 |
5,5680 |
4,6755 |
4,1774 |
3,8550 |
3,6272 |
3,4568 |
3,3239 |
3,2172 |
3,1294 |
2,9931 |
2,8502 |
2,6993 |
2,6203 |
2,5383 |
2,4530 |
2,3637 |
2,2695 |
2,1694 |
|
26 |
7,7213 |
5,5263 |
4,6366 |
4,1400 |
3,8183 |
3,5911 |
3,4210 |
3,2884 |
3,1818 |
3,0941 |
2,9579 |
2,8150 |
2,6640 |
2,5848 |
2,5026 |
2,4170 |
2,3273 |
2,2325 |
2,1315 |
|
27 |
7,6767 |
5,4881 |
4,6009 |
4,1056 |
3,7848 |
3,5580 |
3,3882 |
3,2558 |
3,1494 |
3,0618 |
2,9256 |
2,7827 |
2,6316 |
2,5522 |
2,4699 |
2,3840 |
2,2938 |
2,1984 |
2,0965 |
|
28 |
7,6356 |
5,4529 |
4,5681 |
4,0740 |
3,7539 |
3,527( |
3,3581 |
3,2259 |
3,1195 |
3,0320 |
2,8959 |
2,7530 |
2,6017 |
2,5223 |
2,4397 |
2,3535 |
2,2629 |
2,1670 |
2,0642 |
|
29 |
7,5976 |
5,4205 |
4,5378 |
4,0449 |
3,7254 |
3,4993 |
3,3302 |
3,1982 |
3,0920 |
3,0045 |
2,8685 |
2,7256 |
2,5742 |
2,4946 |
2,4118 |
2,3253 |
2,2344 |
2,1378 |
2,0342 |
|
30 |
7,5625 |
5,3903 |
4,5097 |
4,0179 |
3,6990 |
3,4735 |
3,3045 |
3,1726 |
3,0665 |
2,9791 |
2,8431 |
2,7002 |
2,5487 |
2,4689 |
2,3860 |
2,2992 |
2,2079 |
2,1107 |
2,0062 |
|
40 |
7,3141 |
5,1785 |
4,3126 |
3,8283 |
3,5138 |
3,2910 |
3,1238 |
2,9930 |
2,8876 |
2,8005 |
2,6648 |
2,5216 |
2,3689 |
2,2880 |
2,2034 |
2,1142 |
2,0194 |
1,9172 |
1,8047 |
|
60 |
7,0771 |
4,9774 |
4,1259 |
3,6491 |
3,3389 |
3,1187 |
2,9530 |
2,8233 |
2,7185 |
2,6318 |
2,4961 |
2,3523 |
2,1978 |
2,1154 |
2,0285 |
1,9360 |
1,8363 |
1,7263 |
1,6006 |
|
120 |
6,8510 |
4,7865 |
3,9491 |
3,4796 |
3,1735 |
2,9559 |
2,7918 |
2,6629 |
2,5586 |
2,4721 |
2,3363 |
2,1915 |
2,0346 |
1,9500 |
1,8600 |
1,7628 |
1,6557 |
1,5330 |
1,3805 |
|
¥ |
6,6349 |
4,6052 |
3,7816 |
3,3192 |
3,0173 |
2,8020 |
2,6393 |
2,5113 |
2,4073 |
2,3209 |
2,1848 |
2,0385 |
1,8783 |
1,7908 |
1,6964 |
1,5923 |
1,4730 |
1,3246 |
1,0000 |
(Измененная редакция, Изм. №
1).
Ключевые слова:
статистические методы, прикладная статистика, точечное и интервальное
оценивание, проверка гипотез, нормальное распределение
|
|
|
|




