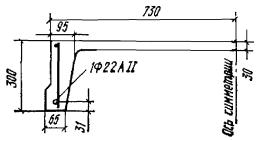
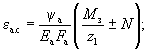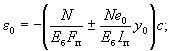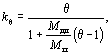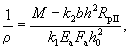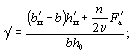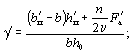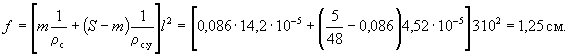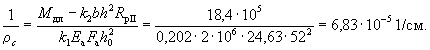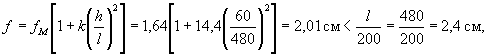|
РУКОВОДСТВО
МОСКВА СТРОЙИЗДАТ 1977 Рекомендовано к изданию
решением секции несущих конструкций НТС ЦНИИПромзданий. (Центр. науч.-исслед. и
проектно-эксперим. ин-т пром. зданий и сооружений ЦНИИПпромзданий Госстроя
СССР. Науч.-исслед. ин-т бетона и железобетона НИИЖБ Госстроя СССР). Руководство по проектированию
бетонных и железобетонных конструкций из тяжелого бетона (без предварительного
напряжения) содержит положения главы СНиП II-21-75, относящиеся к проектированию
этих конструкций, упрощенные методы расчета, а также примеры расчета отдельных
сечений и элементов. Руководство предназначено для
инженеров-проектировщиков, а также для студентов строительных вузов. ПРЕДИСЛОВИЕ
Настоящее Руководство
содержит положения по проектированию бетонных и железобетонных конструкций из
тяжелого бетона, выполняемых без предварительного напряжения арматуры. В Руководстве приведены
требования главы СНиП II-21-75 «Бетонные и железобетонные конструкции»,
относящиеся к проектированию указанных конструкций, и положения, детализирующие
эти требования, а также дополнительные рекомендации по проектированию и
приближенные способы расчета конструкций. В скобках указаны
соответствующие номера пунктов и таблиц главы СНиП II-21-75. При этом формулы,
в которых коэффициенты при расчете элементов конструкций из тяжелого бетона без
предварительного напряжения арматуры имеют однозначную величину (в том числе
при величине, равной 1), приведены с заменой буквенных обозначений
коэффициентов конкретной их величиной. Каждый раздел Руководства
сопровождается примерами расчета конструкций, охватывающими наиболее типичные
случаи, встречающиеся в практике проектирования. В Руководство не включены
данные по проектированию конструкций без предварительного напряжения арматуры,
которые редко встречаются на практике (например, данные для арматуры,
упрочненной вытяжкой, расчет элементов с арматурой, имеющей условный предел
текучести, - классов А-IV, Ат-IV, А-V и Ат-V; расчет
элементов на выносливость). Эти данные приведены в «Руководство по
проектированию предварительно-напряженных железобетонных конструкций из
тяжелого бетона». В Руководстве не приведены
особенности проектирования сборно-монолитных конструкций, элементов с жесткой
арматурой, а также проектирования некоторых специальных сооружений (труб,
силосов и т.п.) и, в частности, вопросы, связанные с определением усилий в этих
конструкциях. Руководство разработано
ЦНИИПромзданий Госстроя СССР (инженеры Б. Ф. Васильев, И. К. Никитин,
Л. Л. Лемыш, А. Г. Королькова) и
НИИЖБ Госстроя СССР (доктора техн. наук А. А. Гвоздев, С. А. Дмитриев и кандидаты техн.
наук Е. А.
Чистяков, Ю. П. Гуща, А.
С. Залесов, Л. К. Руллэ, Н. М.
Мулин, Л. Н. Зайцев, Н. Г. Матков,
Н. И. Катин, И. Е. Евгеньев) с
участием НИЛ ФХММ и ТП Главмоспромстройматериалов (кандидаты техн. наук Э. Г. Ратц, С. Ю.
Цейтлин, Я. М. Якобсон), КТБ
Мосоргстройматериалов (канд. техн. наук В. С. Щукин, инженеры B. Л. Айзинсон, Е. М.
Травкин, Б. И. Фельдман), ДИСИ Минвуз УССР
(канд. техн. наук В. М. Баташев),
ПИСИ Минвуз УССР (канд. техн. наук П. Ф. Вахненко, инж. В. И. Клименко) и Гипростроммаш Минстройдормаша СССР
(инженеры Л. А.
Волков, М. А. Соломович, Т.П. Заневская). ОСНОВНЫЕ БУКВЕННЫЕ
ОБОЗНАЧЕНИЯ
Усилия от внешних нагрузок и
воздействий в поперечном сечении элемента M - изгибающий момент или
момент внешних сил относительно центра тяжести приведенного сечения; N - продольная сила; Q - поперечная сила; Mк - крутящий момент; Mкр, Mдл, Mп -
изгибающие моменты соответственно от кратковременных нагрузок, от постоянных и
длительных нагрузок и от полной нагрузки, включающей постоянную, длительную и
кратковременную нагрузки (при расчете по прочности вводятся с коэффициентом
перегрузки n > 1, в
остальных случаях с n = 1). Характеристики материалов Rпр и RпрII - расчетные сопротивления бетона осевому сжатию
соответственно для предельных состояний первой и второй групп; Rр и RрII - расчетные сопротивления бетона осевому растяжению
соответственно для предельных состояний первой и второй групп; Rа - расчетное сопротивление арматуры растяжению для предельных
состояний первой группы: а) продольной; б) поперечной при расчете
сечений, наклонных к продольной оси элемента, на действие изгибающего момента; Rа.х - расчетное сопротивление поперечной арматуры растяжению для
предельных состояний первой группы при расчете сечений, наклонных к продольной
оси элемента, на действие поперечной силы; Rа.с - расчетное сопротивление арматуры сжатию для
предельных состояний первой группы; RаII - то же, растяжению для
предельных состояний второй группы; Eб - начальный модуль упругости бетона при сжатии и растяжении; Eа - модуль упругости арматуры; n - отношение соответствующих
модулей упругости арматуры Eа
и бетона Eб. Характеристики положения
продольной арматуры в поперечном сечении элемента A - обозначение продольной арматуры: а) при наличии сжатой и
растянутой от действия внешней нагрузки зон сечения - расположенной в
растянутой зоне; б) при полностью сжатом от
действия внешней нагрузки сечении - расположенной у менее сжатой грани сечения; в) при полностью растянутом
от действия внешней нагрузки сечении: для внецентренно-растянутых элементов - расположенной
у более растянутой грани сечения; для центрально-растянутых элементов - всей в
поперечном сечении элемента; A' - обозначение продольной арматуры: а) при наличии сжатой и
растянутой от действия внешней нагрузки зон сечения - расположенной в сжатой
зоне; б) при полностью сжатом от
действия внешней нагрузки сечении - расположенной у более сжатой грани сечения; в) при полностью растянутом
от действия внешней нагрузки сечении внецентренно-растянутых элементов -
расположенной у менее растянутой грани сечения. Геометрические характеристики b -
ширина прямоугольного сечения, ширина ребра таврового и двутаврового сечений; bп и b'п - ширина полки таврового и двутаврового сечений соответственно в
растянутой и сжатой зонах; h - высота прямоугольного, таврового и двутаврового сечений; hп и h'п - высота полки таврового и двутаврового сечений соответственно в
растянутой и сжатой зонах; a и a' - расстояние от равнодействующей усилий
соответственно в арматуре A и
A' до ближайшей грани сечения; h0 - рабочая высота сечения, равная h - a; x - высота сжатой зоны бетона; ξ - относительная высота сжатой зоны бетона, равная u - расстояние между хомутами, намеренное по длине
элемента; uо - расстояние между плоскостями отогнутых стержней,
измеренное по нормали к ним; e0 - эксцентрицитет продольной силы N относительно центра тяжести
приведенного сечения, равный M/N; e и e' - расстояние от точки приложения продольной силы N до равнодействующей усилий
соответственно в арматуре A и
A'; eа - расстояние от точки приложения продольной силы N до центра
тяжести площади сечения арматуры A; l - пролет элемента; l0 - расчетная длина элемента, подвергающегося действию
сжимающей продольной силы; r -
радиус инерции поперечного сечения элемента относительно центра тяжести
сечения; d - номинальный диаметр арматурных стержней; Fа и F'а - площадь сечения арматуры соответственно A и A'; Fх - площадь сечения хомутов, расположенных в одной, нормальной к
продольной оси элемента плоскости, пересекающей наклонное сечение; Fо - площадь сечения отогнутых стержней, расположенных в одной,
наклонной к продольной оси элемента плоскости, пересекающей наклонное сечение; fх - площадь сечения одного стержня хомута; fа - площадь сечения одного стержня продольной арматуры; μ - коэффициент армирования, определяемый как отношение площади
сечения арматуры A к
площади поперечного сечения элемента bh0 без учета сжатых и растянутых
полок; F - площадь всего бетона в поперечном сечении; Fб - площадь сечения сжатой зоны бетона; Fп - площадь приведенного сечения элемента, включающая
площадь бетона и также площадь всей продольной арматуры, умноженную на
отношение модулей упругости арматуры и бетона; Iп - момент инерции приведенного сечения элемента относительно его
центра тяжести; W0 - момент сопротивления приведенного сечения элемента для крайнего
растянутого волокна, определяемый как для упругого материала. 1. ОБЩИЕ УКАЗАНИЯ
ОСНОВНЫЕ
ПОЛОЖЕНИЯ
1.1. Настоящее Руководство
распространяется на проектирование бетонных и железобетонных конструкций из
тяжелого бетона, выполняемых без предварительного напряжения арматуры и
предназначенных для работы в условиях систематического воздействия температур
не выше 50 °С и не ниже минус 70 °С. Тяжелый бетон - бетон плотной
структуры, на цементном вяжущем и плотных заполнителях, крупнозернистый,
тяжелый по объемному весу, при любых условиях твердения. Примечания: 1. Указания настоящего Руководства не распространяются на
проектирование бетонных и железо бетонных конструкций гидротехнических
сооружений, мостов, транспортных тоннелей, труб под насыпями, покрытий
автомобильных дорог и аэродромов. 2. В конструкциях, проектируемых в
соответствии с настоящим Руководством, мелкозернистый бетон применяется только
для заполнения швов в сборных конструкциях, а также для защиты от коррозии
стальных закладных деталей. 1.2(1.2). Проектирование бетонных и
железобетонных конструкций зданий и сооружений, предназначенных для работы в условиях
агрессивной среды и повышенной влажности, должно вестись с учетом
дополнительных требований, предъявляемых главой СНиП по защите строительных
конструкций от коррозии. 1.3(1.3).
Расчетная зимняя температура наружного воздуха
принимается как средняя температура воздуха наиболее холодной пятидневки в
зависимости от района строительства согласно главе СНиП по строительной
климатологии и геофизике. Расчетные технологические температуры устанавливаются
заданием на проектирование. Влажность воздуха окружающей
среды определяется как средняя относительная влажность наружного воздуха
наиболее жаркого месяца в зависимости от района строительства согласно главе
СНиП по строительной климатологии и геофизике или как относительная влажность
внутреннего воздуха помещений отапливаемых зданий и сооружений. 1.4(1.4). Выбор конструктивных решений
должен производиться исходя из технико-экономической целесообразности их
применения в конкретных условиях строительства с учетом максимального снижения
материалоемкости, трудоемкости и стоимости строительства, а также с учетом
условий эксплуатации конструкций. 1.5(1.5). При проектировании зданий и
сооружений должны приниматься конструктивные схемы, обеспечивающие необходимую
прочность, устойчивость и пространственную неизменяемость зданий и сооружений в
целом, а также отдельных конструкций на всех стадиях возведения и эксплуатации. 1.6(1.6). Элементы сборных конструкций
должны отвечать условиям механизированного изготовления на специализированных
предприятиях. Целесообразно укрупнять
элементы сборных конструкций, насколько это позволяют грузоподъемность
монтажных механизмов, а также условия изготовления и транспортирования. 1.7(1.7). Для монолитных конструкций
следует предусматривать унифицированные размеры, позволяющие применять инвентарную опалубку, а
также укрупненные пространственные арматурные каркасы. 1.8(1.8). В сборных конструкциях особое
внимание должно быть обращено на прочность и долговечность соединений. Конструкции узлов и
соединений элементов должны обеспечивать надежную передачу усилий, прочность
самих элементов в зоне стыка, а также связь дополнительно уложенного бетона в
стыке с бетоном конструкции с помощью различных конструктивных и
технологических мероприятий. 1.9(1.9). Бетонные элементы применяются
в конструкциях, работающих преимущественно на сжатие, когда эксцентрицитеты
продольной силы относительно центра тяжести сечения не превышают величин,
указанных в п. 3.4. Изгибаемые бетонные элементы
допускается применять в том случае, когда они лежат на сплошном основании, а
также, как исключение, в других случаях при условии, что они рассчитываются на
нагрузку только от собственного веса и под ними не могут находиться люди и
оборудование. Примечание.
Конструкции рассматриваются как бетонные, если их прочность в стадии
эксплуатации обеспечивается одним бетоном. 1.10(1.10). Численные значения
приведенных в настоящем Руководстве расчетных характеристик бетона и арматуры,
предельно допустимых величин ширины раскрытия трещин и прогибов и т.п.
применяются только при проектировании; для оценки качества конструкций следует
руководствоваться требованиями соответствующих государственных стандартов и
нормативных документов. ОСНОВНЫЕ РАСЧЕТНЫЕ
ТРЕБОВАНИЯ
1.11(1.11). Бетонные и железобетонные
конструкции должны удовлетворять требованиям расчета по несущей способности
(предельные состояния первой группы) и по пригодности к нормальной эксплуатации
(предельные состояния второй группы). а) Расчет по предельным
состояниям первой группы должен обеспечивать конструкции от: хрупкого, вязкого или иного
характера разрушения (расчет по прочности, с учетом в необходимых случаях
прогиба конструкции перед разрушением, неблагоприятного влияния агрессивной
среды, попеременного замораживания и оттаивания и т.п.); усталостного разрушения
(расчет на выносливость конструкций, находящихся под воздействием многократно
повторяющейся нагрузки подвижной или пульсирующей, например рамных фундаментов
и перекрытий под неуравновешенные машины и т.п.); потери устойчивости формы
конструкции (расчет на устойчивость тонкостенных конструкций и т.п.) или ее
положения (расчет на опрокидывание и скольжение подпорных стен,
внецентренно-нагруженных высоких фундаментов; расчет на всплывание заглубленных
или подземных резервуаров, насосных станций и т.п.). б) Расчет по предельным
состояниям второй группы должен обеспечивать конструкции от: образования трещин, а также
их чрезмерного раскрытия (расчет по раскрытию трещин); чрезмерных перемещений -
прогибов, углов поворота, углов перекоса и колебаний (расчет по деформациям). Расчет бетонных конструкций
по предельным состояниям второй группы, а также на выносливость может не
производиться. Примечания: 1. Расчет на действие многократно повторяющейся нагрузки, в том числе
на выносливость, выполняется в соответствии с указаниями «Руководства по
проектированию предварительно-напряженных железобетонных конструкций из
тяжелого бетона». 2. Расчет на устойчивость формы и положения
выполняется по соответствующим нормативным документам или литературным
источникам. 1.12(1.12). Расчет по предельным
состояниям конструкции в целом, а также отдельных ее элементов должен, как
правило, производиться для всех стадий: изготовления, транспортирования,
возведения и эксплуатации, при этом расчетные схемы должны отвечать принятым
конструктивным решениям. Расчет по раскрытию трещин и
по деформациям допускается не производить, если на основании опытной проверки
или практики применения железобетонных конструкций установлено, что величина
раскрытия в них трещин на всех стадиях, перечисленных в настоящем пункте, не
превышает предельно допустимых величин и жесткость конструкций в стадии
эксплуатации достаточна. 1.13(1.13). Величины нагрузок и воздействий, значения коэффициентов перегрузок,
коэффициентов сочетаний, а также подразделение нагрузок на постоянные и
временные - длительные, кратковременные, особые - должны приниматься в
соответствии с требованиями главы СНиП по нагрузкам и воздействиям. Нагрузки,
учитываемые при расчете по предельным состояниям второй группы, должны
приниматься согласно указаниям пп. 1.17 и 1.19. При этом к длительным
нагрузкам следует относить часть полной величины кратковременных нагрузок,
оговоренных в главе СНиП по нагрузкам и воздействиям; а вводимая в расчет
кратковременная нагрузка принимается уменьшенной на величину, учтенную в
длительной нагрузке (например, если снеговая нагрузка составляет: p = p0c
= 100·1,4 = 140 кгс/см2, то снеговая длительная нагрузка будет
равна: pдл = (100 - 70)1,4 = 42 кгс/м2,
а снеговая кратковременная нагрузка: pкр = 140 - 42 = 98 кгс/м2). 1.14(1.14). При расчете элементов
сборных конструкций на воздействие усилий, возникающих при их подъеме,
транспортировании и монтаже, нагрузку от собственного веса элемента следует
вводить в расчет с коэффициентом динамичности, равным: при транспортировании - 1,8; при подъеме и монтаже - 1,5. В этом случае коэффициент
перегрузки к нагрузке от собственного веса элемента не вводится. Для указанных выше
коэффициентов динамичности допускается принимать более низкие значения, если
это подтверждено опытом применения конструкций, но не ниже 1,25. 1.15(1.16). Усилия в статически
неопределимых железобетонных конструкциях от нагрузок и вынужденных перемещений
(вследствие изменения температуры, влажности бетона, смещения опор и т.п.) при
расчете по предельным состояниям первой и второй группы следует, как правило,
определять с учетом неупругих деформаций бетона и арматуры и наличия трещин, а
также с учетом в необходимых случаях деформированного состояния как отдельных
элементов, так и конструкции. Для конструкций, методика
расчета которых с учетом неупругих свойств железобетона не разработана, а также
для промежуточных стадий расчета с учетом неупругих свойств железобетона
(итерационные методы, метод поправочных коэффициентов и т.п.) усилия в
статически неопределимых конструкциях допускается определять в предположении их
линейной упругости. 1.16(1.17).
Ширина кратковременного и длительного
раскрытия трещин для элементов, эксплуатируемых в условиях неагрессивной среды,
не должна превышать величин, приведенных в табл. 1. Таблица 1(1а)
1.17.
Для элементов, указанных в поз. 1 табл. 1(1а), с проволочной рабочей
арматурой классов В-I или Вр-I не допускается образование трещин при действии нагрузки с коэффициентом
перегрузки, большем единицы. 1.18(1.20).
Для железобетонных слабоармированных
элементов, характеризуемых тем, что их несущая способность исчерпывается
одновременно с образованием трещин в бетоне растянутой зоны, площадь сечения
продольной растянутой арматуры должна быть увеличена по сравнению с требуемой
из расчета по прочности не менее чем на 15 %. Такое увеличение армирования
следует производить при выполнении условия Mт ≥ Mпр, где Mт - момент трещинообразования,
определяемый согласно п. 4.3 с заменой значения RрII
на 1,2RрII; Mпр - момент, соответствующий исчерпанию несущей способности,
определяемый согласно пп. 3.16 - 3.82; для внецентренно-сжатых и
растянутых элементов значения Mпр определяются относительно
оси, проходящей через ядровую точку, наиболее удаленную от растянутой зоны (см.
п. 4.3). 1.19(1.21).
Прогибы элементов железобетонных конструкций
не должны превышать предельно допустимых величин, устанавливаемых с учетом
следующих требований: а) технологических (условия
нормальной работы кранов, технологических установок, машин и т.п.); б) конструктивных (влияние
соседних элементов, ограничивающих деформации; необходимость выдерживания
заданных уклонов и т.п.); в) эстетических (впечатление
людей о пригодности конструкции). Таблица 2(2)
Величины предельно допустимых
прогибов приведены в табл. 2. Расчет прогибов должен
производиться: при ограничении технологическими или конструктивными
требованиями - на действие постоянных, длительных и кратковременных нагрузок;
при ограничении эстетическими требованиями - на действие постоянных и
длительных нагрузок. При этом коэффициент перегрузки n принимается равным единице. Для не защищенных от
солнечной радиации конструкций, предназначенных для эксплуатации в
климатическом подрайоне IVA,
согласно главе СНиП по строительной климатологии и геофизике, при определении
перемещений необходимо учитывать температурные климатические воздействия. Для железобетонных элементов,
выполняемых со строительным подъемом, значения предельно допустимых прогибов
могут быть увеличены на высоту строительного подъема, если это не
ограничивается технологическими или конструктивными требованиями. Величины предельно допустимых
прогибов в других случаях (не предусмотренных табл. 2) устанавливаются по
специальным требованиям, но при этом они не должны превышать 1/150
пролета и 1/75 вылета консоли. Если в нижележащем помещении
с гладким потолкам имеются расположенные поперек пролета элемента l
постоянные перегородки (не являющиеся опорами) с расстоянием между ними lп, то прогиб элемента в
пределах расстояний lп (отсчитываемый от линии,
соединяющей верхние точки осей перегородок) может быть допущен до 1/200lп, однако при этом предельный
прогиб всего элемента должен быть не более 1/150l. 1.20(1.21). Для не связанных с соседними
элементами железобетонных плит перекрытий, лестничных маршей, площадок и т.п.
должна производиться дополнительная проверка по зыбкости: дополнительный прогиб
от кратковременно действующей сосредоточенной нагрузки 100 кгс при наиболее
невыгодной схеме ее приложения должен быть не более 0,7 мм. 1.21(1.23). Расстояния между
температурно-усадочными швами должны устанавливаться расчетом. Расчет
допускается не производить при расчетных зимних температурах наружного воздуха
выше минус 40 °С, если принятые расстояния между температурно-усадочными швами
не превышают величин, приведенных в табл. 3. 1.22. При расчете перекрытия по
предельным состояниям второй группы вес перегородок учитывается следующим
образом: а) нагрузка от веса жестких
перегородок (например, железобетонных сборных, выполняемых из горизонтальных
элементов, железобетонных и бетонных, монолитных, каменных и т.п.) принимается
сосредоточенной по концам перегородки, а при наличии проемов - и у краев
проема; б) для прочих перегородок -
60 % их веса принимаются распределенными по длине перегородки (на участках
между проемами), а 40 % - сосредоточенными по концам перегородки и у краев
проема. 1.23. Распределение местной
нагрузки между элементами сборных перекрытий, выполняемых из многопустотных или
сплошных плит, при условии обеспечения качественной заливки швов между плитами,
допускается производить с учетом нижеследующих указаний: Таблица 3(3)
а) при расчете по всем
предельным состояниям принимается следующее распределение нагрузки от веса
перегородок, расположенных вдоль пролета равных по ширине плит: если перегородка расположена
в пределах одной плиты, то на эту плиту передается 50 % веса перегородки, а по
25 % ее веса передаются на две смежные плиты; если перегородка опирается на
две соседние плиты, то вес перегородки распределяется поровну между ними; б) при расчете по предельным
состояниям второй группы местные сосредоточенные нагрузки, расположенные в
пределах средней трети пролета плиты, распределяются на ширину, не превышающую
длины этого пролета; при расчете по прочности такое распределение
сосредоточенных нагрузок может быть допущено лишь при условии соединения
смежных плит по длине шпонками, проверяемыми расчетом (см. п. 3.114). 2. МАТЕРИАЛЫ ДЛЯ БЕТОННЫХ И ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙБЕТОН
2.1(2.3). Для бетонных и
железобетонных конструкций должны предусматриваться следующие проектные марки
тяжелого бетона: а) по прочности на сжатие - М
50, М 75, М 100, М 150, М 200, М 250, М 300, М 350, М 400, М 450, М 500, М 600,
М 700, М 800 (при этом проектные марки М 250, М 350 и М 450 следует
предусматривать при условии, что это приводит к экономии цемента по сравнению с
применением бетона проектных марок соответственно М 300, М 400, М 500 и не
снижает другие технико-экономические показатели конструкции); б) по морозостойкости - Мрз
50, Мрз 75, Мрз 100, Мрз 150, Мрз 200, Мрз 300, Мрз 400, Мрз 500; в) по водонепроницаемости - В
2, В 4, В 6, В 8, В 10, В 12. Примечания: 1. Проектной маркой бетона по какому-либо признаку называется значение
соответствующей характеристики бетона, задаваемое при проектировании. 2. Соответствие фактического значения
характеристики бетона его проектной марке устанавливается на основании
результатов испытаний согласно требованиям соответствующих государственных
стандартов. 2.2(2.4). Срок твердения (возраст)
бетона, отвечающий его проектной марке по прочности на сжатие, принимается, как
правило, 28 дней. В тех случаях, когда известны
сроки фактического загружения конструкций, способы их возведения, условия
твердения бетона, сорт применяемого цемента, допускается устанавливать
проектную марку бетона в ином возрасте (большем или меньшем); при этом для
монолитных массивных бетонных и железобетонных конструкций всегда должен
учитываться возможный реальный срок их загружения проектными нагрузками. Величина отпускной прочности
бетона в элементах сборных конструкций должна назначаться минимально допустимой
(в зависимости от условий транспортирования, монтажа и срока загружения
изделий, технологии их изготовления, климатических условий строительства и
времени года) в соответствии с указаниями государственных стандартов на сборные
изделия. 2.3(2.5). Для железобетонных
конструкций не допускается применение бетона проектной марки ниже М 100; Рекомендуется принимать
проектную марку бетона: для железобетонных сжатых
стержневых элементов - не ниже М 200; для сильно нагруженных сжатых
стержневых элементов (например, для колонн, воспринимающих значительные
крановые нагрузки, и для колонн нижних этажей многоэтажных зданий) - не ниже М
300; для тонкостенных
железобетонных конструкций, а также для стен зданий и сооружений, возводимых в
скользящей и переставной опалубке, - не ниже М 200. Для бетонных сжатых элементов
не рекомендуется применять бетон проектной марки выше М 400. Таблица 4(8)
2.4(2.8).
Для замоноличивания стыков элементов сборных
железобетонных конструкций проектную марку бетона следует устанавливать в
зависимости от условий работы соединяемых элементов, но принимать не ниже М
100. 2.5(2.9).
Проектные марки бетона по морозостойкости и
водонепроницаемости бетонных и железобетонных конструкций в зависимости от
режима их эксплуатации и значений расчетных зимних температур наружного воздуха
в районе строительства должны приниматься: для конструкций зданий и
сооружений (кроме наружных стен отапливаемых зданий) - не ниже указанных в
табл. 4(8); для наружных стен
отапливаемых зданий - не ниже указанных в табл. 5(9). 2.6(2.10). Для замоноличивания стыков
элементов сборных конструкций, которые в процессе эксплуатации или монтажа
могут подвергаться воздействию отрицательных температур наружного воздуха,
следует применять бетоны проектных марок по морозостойкости и
водонепроницаемости не ниже принятых для стыкуемых элементов. Нормативные и
расчетные характеристики бетона
2.7(2.11). Нормативными сопротивлениями
бетона являются: сопротивление осевому сжатию кубов (кубиковая прочность) Rн; сопротивление осевому сжатию
призм (призменная прочность) Rнпр; сопротивление осевому
растяжению Rнр. Нормативные сопротивления
бетона Rнпр и Rнр в зависимости от проектной
марки бетона по прочности на сжатие даны в табл. 6(11). 2.8(2.13). Расчетные сопротивления
бетона для предельных состояний первой группы Rпр и Rр определяются путем деления
нормативных сопротивлений на коэффициенты безопасности по бетону, принимаемые
равными: при сжатии kб.с = 1,3; при растяжении kб.р = 1,5. Расчетные сопротивления
бетона Rпр и Rр снижаются (или повышаются)
путем умножения на коэффициенты условий работы бетона mб, учитывающие: особенности
свойств бетонов, длительность действия нагрузки и ее многократную
повторяемость, условия и стадию работы конструкции, способ ее изготовления,
размеры сечения и т.п. Расчетные сопротивления
бетона для предельных состояний второй группы RпрII и RрII принимаются равными нормативным сопротивлениям и
вводятся в расчет с коэффициентом условий работы бетона mб = 1. Величины расчетных
сопротивлений бетона в зависимости от проектных марок по прочности на сжатие
приведены (с округлением) для предельных состояний первой группы в табл. 7, для
предельных состояний второй группы - в табл. 6(11). В расчетные сопротивления,
приведенные в табл. 7, включены следующие коэффициенты условий работы mб: а) для высокопрочного бетона
проектных марок М 600, М 700 и М 800 в расчетные сопротивления бетона сжатию Rпр - коэффициент mб, равный соответственно 0,95,
0,925 и 0,9; Таблица 5(9)
б) для бетонных конструкций в
расчетные сопротивления бетона сжатию и растяжению Rпр и Rр - коэффициент mб = 0,9; в) в расчетные сопротивления
бетона сжатию и растяжению - коэффициент mб1, учитывающий влияние
длительности действия нагрузок и условия нарастания прочности бетона во
времени; порядок использования коэффициентов mб1 в расчете приведен в п. 3.1. Таблица
6(11)
Таблица 7
Расчетные сопротивления
бетона, приведенные в табл. 7, в соответствующих случаях
следует умножать на коэффициенты условий работы бетона согласно табл. 8(15). Таблица 8(15)
2.9(2.14). Для мелкозернистого бетона
нормативные и расчетные сопротивления принимаются равными соответствующим
значениям для тяжелого бетона, указанным в табл. 6(11) и 7. При этом должны учитываться
соответствующие коэффициенты условий работы та согласно табл. 8(15) и 9(17). 2.10(2.15). Величины начального модуля
упругости бетона Eб при сжатии и растяжении принимаются по
табл. 10(18). Для незащищенных от солнечной
радиации конструкций, предназначенных для работы в климатическом подрайоне IVA
согласно главе СНиП по строительной климатологии и геофизике, значения Eб, указанные в табл. 10(18),
следует умножать на коэффициент 0,85. Для бетона, подвергнутого автоклавной
обработке, значение Eб,
указанное в табл. 10(18) для бетона естественного твердения,
следует умножать на коэффициент 0,75. При наличии данных о сорте
цемента, составе бетона, условиях изготовления (например, центрифугированный
бетон) и т.д. допускается принимать другие значения Eб, согласованные в установленном
порядке. Таблица 9(17)
Таблица 10(18)
2.11(2.16). Коэффициент линейной
температурной деформации αбt при изменении температуры от минус 50 °С до плюс 50
°С принимается равным 1·10-5 град-1. При наличии данных о
минералогическом составе заполнителей, расходе цемента, степени водонасыщения
бетона, морозостойкости и т.д. допускается принимать другие значения αбt, обоснованные в
установленном порядке. 2.12(2.17). Начальный коэффициент поперечной деформации бетона (коэффициент
Пуассона) μ принимается равным 0,2 для всех видов бетона, а модуль сдвига бетона G - равным 0,4 от соответствующих значений Eб, указанных в табл. 10(18). 2.13. Объемный вес тяжелого
вибрированного бетона на гравии или щебне из природного камня принимается
равным 2400 кг/м3. Объемный вес железобетона при
содержании арматуры 3 % и менее может приниматься равным 2500 кг/м3;
при содержании арматуры более 3 % объемный вес должен определяться как сумма
весов бетона и арматуры на единицу объема железобетонной конструкции. При этом
вес арматурной стали на единицу длины принимается по табл. 1 прил. 2; вес
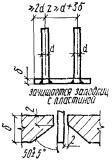
полосовой, угловой и фасонной стали по действующим ГОСТам. АРМАТУРА И ЗАКЛАДНЫЕ
ДЕТАЛИ
Виды
арматурных сталей
2.14(2.18). Для армирования железобетонных
конструкций, выполняемых без предварительного напряжения, применяется арматура,
отвечающая требованиям соответствующих государственных стандартов (см. табл. 11),
следующих видов и классов: а) стержневая горячекатаная
арматура: гладкая класса А-I, периодического профиля
классов А-II и А-III; б) обыкновенная арматурная
проволока: гладкая класса В-I, периодического профиля
класса Вр-I. Для закладных деталей и
соединительных накладок применяется, как правило, прокатная углеродистая сталь
класса С38/23 согласно главе СНиП по проектированию стальных конструкций. В качестве арматуры
железобетонных конструкций допускается применять другие виды сталей, применение
которых должно быть согласовано в установленном порядке. Примечание. В дальнейшем в настоящем Руководстве для краткости используются
следующие термины: «стержень»
- для обозначения арматуры любого диаметра, вида и профиля независимо от того,
поставляется ли она в прутках или в мотках (бунтах); «диаметр» d, если не оговорено особо, означает номинальный
диаметр стержня. 2.15(2.20). В качестве ненапрягаемой
арматуры железобетонных конструкций [кроме указанных в п. 2.16(2.21)]
следует преимущественно применять: а) горячекатаную арматурную
сталь класса А-III; б) обыкновенную арматурную
проволоку диаметром 3 - 5 мм классов Вр-I и В-I (в сварных сетках и
каркасах); допускается также применять: в) горячекатаную арматурную
сталь классов А-II и А-I в основном для поперечной
арматуры линейных элементов, для конструктивной и монтажной арматуры, а также в
качестве продольной рабочей арматуры в случаях, когда использование других
видов арматуры нецелесообразно или не допускается; г) обыкновенную арматурную
проволоку класса В-I диаметром 3 - 5 мм - для вязаных хомутов балок
высотой до 400 мм и колонн. Арматуру классов А-III, А-II и А-I
рекомендуется применять в виде сварных каркасов и сварных сеток. При обосновании экономической
целесообразности допускается применять ненапрягаемую арматуру классов А-IV, Ат-IV, А-V и Ат-V в
качестве сжатой арматуры, а классов А-IV, Ат-IV и в качестве растянутой.
Кроме того, в качестве растянутой арматуры допускается применение арматуры
класса А-IIIв. Расчет элементов с применением арматуры перечисленных
классов выполняется в соответствии с указаниями «Руководства по проектированию
предварительно-напряженных железобетонных конструкций из тяжелого бетона». 2.16(2.21).
В конструкциях с ненапрягаёмой арматурой,
находящихся под давлением газов или жидкостей, следует преимущественно
применять: а) горячекатаную арматурную
сталь классов А-II и А-I; допускается также применять: б) горячекатаную арматурную
сталь класса А-III; в) обыкновенную арматурную
проволоку классов Вр-I и В-I. 2.17(2.24). При выборе вида и марок стали
для арматуры, устанавливаемой по расчету, а также прокатных сталей для
закладных деталей должны учитываться температурные условия эксплуатации
конструкций и характер их нагружения согласно табл. 11 и 12. При возведении в условиях
расчетных зимних температур наружного воздуха ниже минус 40 °С конструкций с
арматурой, допускаемой для использования только в отапливаемых зданиях, должна
быть обеспечена несущая способность конструкции на стадии ее возведения, при
этом расчетное сопротивление арматуры принимается с коэффициентом 0,7, а
расчетная нагрузка - с коэффициентом перегрузки n = 1. 2.18(2.25).
Для монтажных (подъемных) петель элементов
сборных железобетонных и бетонных конструкций должна применяться горячекатаная
арматурная сталь класса А-II марки 10ГТ и класса А-I марок ВСт3сп2 и ВСт3пс2. В случае если возможен монтаж
конструкций при расчетной зимней температуре ниже минус 40 °С, для монтажных петель
не допускается применять сталь марки ВСт3пс2. Таблица 11 (прил. 3) ДАННЫЕ ПО АРМАТУРНЫМ СТАЛЯМ Основные виды арматурных
сталей и области их применения в железобетонных конструкциях в зависимости от
характера действующих нагрузок и расчетных температур (знак «+» означает
«допускается», знак «-» - «не допускается»)
Таблица 12 (прил. 4) Области применения
углеродистых сталей для закладных деталей железобетонных и бетонных конструкций
Нормативные и
расчетные характеристики арматуры
2.19(2.26). За нормативные сопротивления
арматуры Rна принимаются наименьшие
контролируемые значения: для стержневой арматуры -
предела текучести, физического или условного (равного величине напряжений,
соответствующих остаточному относительному удлинению 0,2 %); для проволочной арматуры -
временного сопротивления разрыву. Указанные контролируемые
характеристики арматуры принимаются в соответствии с государственными
стандартами или техническими условиями на арматурные стали и гарантируются с вероятностью не
менее 0,95. Нормативные сопротивления Rна для основных видов
ненапрягаемой арматуры приведены в табл. 13(19, 20). 2.20(2.27). Расчетные сопротивления
арматуры растяжению и сжатию Rа и Rа.с для предельных состояний
первой группы определяются путем деления нормативных сопротивлений на
коэффициенты безопасности по арматуре, принимаемые равными: а) для стержневой арматуры
классов: А-I и А-III - kа = 1,55; А-II - kа = 1,1; б) для проволочной арматуры
классов: Вр-I - kа = 1,55; В-I - kа = 1,75. Расчетные сопротивления
арматуры растяжению для предельных состояний второй группы RаII
принимаются равными нормативным сопротивлениям. Расчетные сопротивления
арматуры растяжению и сжатию для основных видов ненапрягаемой арматуры при
расчете конструкций по предельным состояниям первой группы приведены в табл. 14(22,
23), а при расчете по предельным состояниям второй группы - в табл. 13(19,
20). Таблица 13(19, 20)
2.21(2.29). В расчетные сопротивления Rа.х, приведенные в табл. 14(22,
23), включены следующие коэффициенты условий работы mа.х, учитывающие особенности
работы поперечной арматуры (хомутов и отогнутых стержней) на действие
поперечной силы: независимо от вида и класса
арматуры - коэффициент mа.х = 0,8, учитывающий
неравномерность распределения напряжений в арматуре по длине наклонного
сечения; при применении стержневой
арматуры класса А-III диаметром менее 1/3 диаметра
продольных стержней и проволочной арматуры классов В-I и Вр-I в
сварных каркасах - коэффициент mа.х = 0,9, учитывающий
возможность хрупкого разрушения сварного соединения; при применении проволочной
арматуры класса В-I в вязаных каркасах - коэффициент mа.х = 0,75, учитывающий ее
пониженное сцепление с бетоном. Таблица 14(22, 23)
Таблица 15(29)
Кроме того, при расположении
рассматриваемого сечения в зоне анкеровки арматуры расчетные сопротивления Rа и Rа.с умножаются на коэффициент
условий работы mа3, учитывающий неполную анкеровку арматуры и
определяемый согласно п. 3.46. 2.22(2.31). Величины модуля упругости
арматуры Eа принимаются по табл. 15(29). 3. РАСЧЕТ ЭЛЕМЕНТОВ
БЕТОННЫХ И ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ПЕРВОЙ ГРУППЫ
3.1. С целью учета влияния вероятной длительности действия нагрузок на
прочность бетона расчет бетонных и железобетонных элементов по прочности в
общем случае производится: а) на действие постоянных,
длительных и кратковременных нагрузок, кроме нагрузок, суммарная длительность
действия которых мала (ветровые нагрузки, крановые нагрузки, нагрузки от
транспортных средств, нагрузки, возникающие при изготовлении, транспортировании
и возведении и т.п.), а также на действие особых нагрузок, вызванных
деформациями просадочных, набухающих, вечномерзлых и т.п. грунтов; в этом
случае расчетные сопротивления бетона сжатию и растяжению Rпр и Rр принимаются по табл. 7 при mб1 = 0,85; б) на действие всех нагрузок,
включая нагрузки, суммарная длительность действия которых мала; в этом случае
расчетные сопротивления бетона Rпр и Rр принимаются по табл. 7 при mб1 = 1,1*. Если конструкция
эксплуатируется в условиях, благоприятных для нарастания прочности бетона
(твердение под водой, во влажном грунте или при влажности окружающего воздуха
выше 75 %, см. п. 1.3), расчет по случаю «а» производится при mб1 = 1. Условия прочности должны
выполняться при расчете как по случаю «а», так и по случаю «б». При отсутствии нагрузок с
малой суммарной длительностью действия, а также аварийных нагрузок расчет
прочности производится только по случаю «а». При наличии нагрузок с малой
суммарной длительностью действия или аварийных нагрузок расчет производятся
только по случаю «б», если выполняется условие PI ≤ 0,77PII, (1) где PI - усилие
(момент MI или
поперечная сила QI) от нагрузок, используемых
при расчете по случаю «а»; при этом в расчете сечений, нормальных к продольной
оси внецентренно-нагруженных элементов, момент MI
принимается относительно оси, проходящей через наиболее растянутый (или менее
сжатый) стержень арматуры, а для бетонных элементов - относительно растянутой
или наименее сжатой грани; PII - то же, от
нагрузок, используемых при расчете по случаю «б». Допускается производить
расчет только по случаю «б» и при невыполнении условия (1), умножая расчетные
сопротивления бетона Rпр и Rр (при mб1 = 1) на коэффициент mб.д = 0,85PII/PI ≤ 1,1. Для внецентренно-сжатых
элементов, рассчитываемых по недеформированной схеме, значения PI и PII можно определять без учета прогиба элемента. Для конструкций,
эксплуатируемых в условиях, благоприятных для нарастания прочности бетона,
условие (1)
приобретает вид PI < 0,9PII, а коэффициент mб.д принимают равным mб.д = PII/PI. РАСЧЕТ БЕТОННЫХ
ЭЛЕМЕНТОВ ПО ПРОЧНОСТИ
3.2(3.1). Расчет по прочности элементов бетонных конструкций должен производиться
для сечений, нормальных к их продольной оси. В зависимости от условий работы
элементов они рассчитываются как без учета, так и с учетом сопротивления бетона
растянутой зоны. Без учета сопротивления
бетона растянутой зоны производится расчет внецентренно-сжатых элементов,
принимая, что достижение предельного состояния характеризуется разрушением
сжатого бетона. С учетом сопротивления бетона
растянутой зоны производится расчет изгибаемых элементов, а также
внецентренно-сжатых элементов, в которых не допускаются трещины из условий
эксплуатации конструкций (элементы, подвергающиеся давлению воды, карнизы,
парапеты и др.). При этом принимается, что достижение предельного состояния характеризуется
разрушением бетона растянутой зоны (появлением трещин). В случаях когда вероятно
образование наклонных трещин (например, элементы двутаврового и таврового
сечений при наличии поперечных сил), должен производиться расчет бетонных
элементов из условия (13) п. 3.10. Кроме того, должен
производиться расчет элементов на местное действие нагрузки (смятие) согласно
п. 3.95. Внецентренно-сжатые
элементы
3.3(3.2, 1.22). При расчете
внецентренно-сжатых бетонных элементов должен приниматься во внимание случайный
эксцентрицитет продольного усилия e0сл, обусловленный неучтенными в расчете
факторами, в том числе неоднородностью свойств бетона по сечению. Эксцентрицитет e0сл в любом случае принимается не менее
следующих значений: 1/400 всей длины
элемента или длины его части (между точками закрепления элемента), учитываемой
в расчете; 1/30 высоты сечения
элемента; 1 см. Для элементов статически
неопределимых конструкций (например, защемленные по концам стены или столбы)
величина эксцентрицитета продольной силы относительно центра тяжести сечения e0 принимается
равной эксцентрицитету, полученному из статического расчета конструкции, но не
менее e0сл. В элементах статически
определимых конструкций эксцентрицитет e0 находится как сумма эксцентрицитетов - определяемого из
статического расчета конструкции и случайного. 3.4(3.3). При гибкости элементов l0/r > 14 (для прямоугольных сечений при l0/h > 4) необходимо учитывать влияние на их несущую способность прогибов
как в плоскости эксцентрицитета продольного усилия, так и в нормальной к ней
плоскости путем умножения значений e0 на коэффициент η (см. п. 3.7); в случае расчета из
плоскости эксцентрицитета продольного усилия значение e0
принимается равным величине случайного эксцентрицитета. Применение
внецентренно-сжатых бетонных элементов не допускается при эксцентрицитетах
приложения продольной силы с учетом прогибов, e0η, превышающих: при основном сочетании
нагрузок - 0,9y; при особом сочетании нагрузок
- 0,95y, но в любом случае (y - 1) см, где y - расстояние от центра тяжести сечения до наиболее
сжатого волокна бетона. 3.5(3.4). Во внецентренно-сжатых
бетонных элементах в случаях, указанных в п. 5.126, необходимо
предусматривать конструктивную арматуру. 3.6(3.5). Расчет внецентренно-сжатых
бетонных элементов должен производиться из условия N
≤ RпрFб, (2) где Fб - определяется из условия,
что ее центр тяжести совпадает с точкой приложения равнодействующей внешних сил
(рис. 1). Для элементов прямоугольного
сечения Fб определяется по формуле При марках бетона М 400 и
выше не следует пользоваться условием (2). Внецентренно-сжатые бетонные
элементы, в которых не допускается появление трещин (см. п. 3.2),
независимо от расчета из условия (2) должны быть проверены с учетом сопротивления
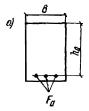
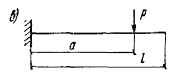
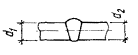
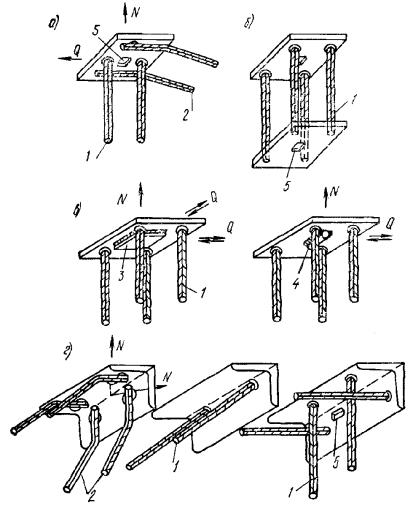
бетона растянутой зоны из условия Рис. 1. Схема расположения
усилий и эпюра напряжений в поперечном сечении внецентренно-сжатого бетонного
элемента без учета сопротивления бетона растянутой зоны 1 - центр тяжести площади сжатой зоны; 2 - центр тяжести площади
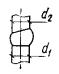
сечения Рис. 2. К определению Wт 1 - нулевая линия Для элементов прямоугольного
сечения условие (4) имеет вид η - коэффициент, определяемый по формуле (8); rу - расстояние от центра тяжести сечения до ядровой точки, наиболее
удаленной от растянутой зоны, определяемое по формуле
Wт - момент сопротивления сечения для крайнего растянутого волокна,
определяемый с учетом неупругих деформаций растянутого бетона в предположении
отсутствия продольной силы по формуле где Iб.0 - момент инерции сжатой зоны бетона относительно нулевой линии; Sб.р - статический момент растянутой зоны бетона относительно нулевой
линии; h - x - расстояние от нулевой линии до
растянутой грани, равное
здесь Fи - площадь
сжатой зоны бетона, дополненная в растянутой зоне прямоугольником шириной b, равной ширине сечения по нулевой линии, и высотой h - x (рис. 2); Sи - статический момент площади Fи относительно растянутой
грани. Допускается значение Wт определять по формуле Wт =
γW0, 3.7(3.6). Значение коэффициента η,
учитывающего влияние прогиба на величину
эксцентрицитета продольного усилия e0, следует
определять по формуле где Nкр - условная критическая сила,
определяемая по формуле (I -
момент инерции бетонного сечения относительно центра тяжести сечения). Для элементов прямоугольного
сечения формула (9) имеет вид kдл - коэффициент, учитывающий влияние длительного действия нагрузки на
прогиб элемента в предельном состоянии, равный
здесь M1 -
момент относительно растянутой или наименее сжатой грани сечения от действия
полной нагрузки; M1дл - то же, от действия постоянных и длительных нагрузок; l0 - определяется по табл. 16(31); t - коэффициент, принимаемый
равным e0/h, но не менее величины tмин = 0,5 - 0,01(l0/h) - 0,001Rпр. Здесь Rпр - в кгс/см2. Примечание.
При расчете сечения как по случаю «а», так и по случаю «б» (см. п. 3.1)
допускается значение tмин определять один раз, принимая значение mб1 = 1. Таблица 16(31)
3.8. Расчет внецентренно-сжатых
бетонных элементов прямоугольного сечения с учетом прогиба при марке бетона не
выше М 250 допускается производить при помощи графика на рис. 3. При этом должно выполняться
условие: N
≤ n1Rпрbh, где n1 - определяется по графику
рис. 3
в зависимости от значений e0/h и λ = l0/h. 3.9(3.7). Расчет элементов бетонных
конструкций на местное сжатие (смятие) должен производиться согласно указаниям
пп. 3.95
и 3.96. Рис. 3. График несущей
способности внецентренно-сжатых бетонных элементов (сплошная линия - при M1дл/M1
= 1, пунктирная - при M1дл/M1 =
0,5) Изгибаемые
элементы
3.10(3.8). Расчет изгибаемых бетонных элементов должен производиться из условия M ≤ RрWт, (11) где Wт - определяется по формуле (7); для
элементов прямоугольного сечения значение Wт принимается равным
Кроме того, для элементов
таврового и двутаврового сечений должно выполняться условие τ
≤ Rр, (13) где τ - касательные напряжения,
определяемые как для упругого материала на уровне центра тяжести сечения. РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ
ЭЛЕМЕНТОВ ПО ПРОЧНОСТИ
3.11(3.9). Расчет по прочности
элементов железобетонных конструкций должен производиться для сечений,
нормальных к их продольной оси, а также для наклонных к ней сечений наиболее
опасного направления; при наличии крутящих моментов следует проверить прочность
пространственных сечений, ограниченных в растянутой зоне спиральной трещиной,
наиболее опасного из возможных направлений. Кроме того, должен производиться
расчет элементов на местное действие нагрузки (смятие, продавливание, отрыв). Изгибаемые элементы
Расчет
сечений, нормальных к продольной оси элемента
Общие указания
3.12(3.11).
Расчет сечений, нормальных к продольной оси
элемента, когда изгибающий момент действует в плоскости оси симметрии сечения и
арматура сосредоточена у перпендикулярных к указанной плоскости граней
элемента, должен производиться в зависимости от соотношения между величиной
относительной высоты сжатой зоны бетона ξ = x/h0, определяемой из
соответствующих условий равновесия, и граничным значением относительной высоты
сжатой зоны бетона ξR (см. п. 3.15), при котором предельное состояние элемента наступает одновременно с
достижением в растянутой арматуре напряжения, равного расчетному сопротивлению Rа. 3.13(3.18).
Расчет изгибаемых элементов кольцевого сечения
при соотношении внутреннего и наружного радиусов r1/r2 ≥ 0,5 с арматурой,
равномерно распределенной по длине окружности (при числе продольных стержней не
менее 6), должен производиться как для внецентренно-сжатых элементов согласно
пп. 3.71 и 3.72, принимая величину продольной силы N = 0 и
подставляя вместо Ne0 значение
изгибающего момента M. 3.14.
Расчет нормальных сечений, не оговоренных в
пп. 3.12, 3.13, а также в п. 3.25, следует производить, пользуясь формулами для общего случая расчета
нормального сечения внецентренно-сжатого элемента (п. 3.78), принимая в формуле (138) N = 0 и заменяя в условии (137) значение 3.15(3.12).
Граничное значение относительной высоты сжатой
зоны бетона ξR определяется по формуле
где ξ0 - характеристика сжатой зоны
бетона, равная: ξ0 = 0,85 - 0,0008Rпр; (15) σε = 5000 - при использовании
коэффициента условий работы бетона mб1 = 0,85 (см. п. 3.1); σε = 4000 - при использовании
коэффициента mб1 = 1 или mб1 = 1,1; Rпр и Rа - в кгс/см2. Значения ξ0 и
ξR, отвечающие вышеприведенным формулам, даны в табл. 17. Таблица 17
Прямоугольные
сечения
3.16. Расчет прямоугольных сечений с арматурой, сосредоточенной у сжатой и
растянутой граней элемента (рис. 4), производится следующим образом в зависимости от высоты сжатой зоны а) при ξ = x/h0 ≤ ξR - из условия M ≤ Rпрbx(h0 - 0,5x) + Rа.сF'а(h0 - a'); (17) б) при ξ
> ξR - из условия M ≤ ARRпрbh02 + Rа.сF'а(h0 - a'), (18) где AR = ξR(1 - 0,5ξR). При этом расчетную несущую
способность сечения можно несколько увеличить путем замены в условии (18)
значения AR на (0,8AR + 0,2A0), где
A0 = ξ(1 - 0,5ξ)
при ξ ≤ 1 или см. табл. 18. Значения ξR и AR определяются по табл. 17. Если x
≤ 0, то прочность проверяется из условия M ≤ RаFа(h0 - a'). (19) Примечание.
Если высота сжатой зоны, определенная с учетом половины сжатой арматуры
то расчетную несущую способность сечения можно
несколько увеличить, производя расчет по формулам (16) и (17) без учета сжатой арматуры. 3.17. Изгибаемые элементы рекомендуется проектировать так, чтобы обеспечить
выполнение условия ξ < ξR. Невыполнение этого условия можно допустить в случае, когда площадь
сечения растянутой арматуры определена из расчета по предельным состояниям
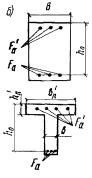
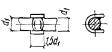
второй группы или принята по конструктивным соображениям. Рис. 4. Схема расположения
усилий в поперечном прямоугольном сечении изгибаемого железобетонного элемента 3.18. Проверка прочности прямоугольных сечений с одиночной арматурой
производится: при x ≤ ξRh0 - из условия M ≤ RаFа(h0 - 0,5x), (20) где высота сжатой зоны равна
при x
> ξRh0 - из условия M
≤ ARRпрbh02, (21) при этом расчетная несущая способность сечения может
быть несколько увеличена, если использовать указание п. 3.16 «б». Здесь ξR и AR - см.
п. 3.15
или табл. 17. 3.19. Подбор продольной арматуры производится следующим образом. Вычисляется значение Если A0 ≤ AR (см. табл. 17), то сжатой арматуры по расчету не требуется. В этом случае (при отсутствии
сжатой арматуры) площадь сечения растянутой арматуры определяется по формуле где υ -
определяется по табл. 18 в зависимости от значения A0. Если A0 > AR, то требуется увеличить сечение, повысить марку бетона или установить
сжатую арматуру согласно указаниям п. 3.20. При учете коэффициента
условия работы бетона mб1 = 0,85 (см. п. 3.1)
подбор растянутой арматуры можно также производить, пользуясь прил. 1. 3.20. Если по расчету требуется сжатая арматура (см. п. 3.19), то площади сечений
растянутой и сжатой арматуры, соответствующие минимуму их суммы, для элементов
из бетона марки М 400 и ниже рекомендуется определять по формулам: Если принятая площадь сечения
сжатой арматуры F'а значительно превышает ее
значение, вычисленное по формуле (24), то площадь сечения растянутой арматуры
определяется с учетом фактического значения площади F'а по формуле Fа = ξbh0Rпр/Rа + F'а, (26) где ξ - определяется по табл. 18 в
зависимости от значения
которое должно удовлетворять условию A0 ≤ AR (см. табл. 17). Примечание.
При марках бетона выше М 400 в формулах (24) и (25) значения 0,4 и 0,55
заменяются соответственно на значения AR и ξR, принимаемые не более 0,4 и 0,55. Таблица 18
Тавровые и двутавровые сечения
3.21(3.16). Расчет сечений, имеющих полку в сжатой зоне (тавровых, двутавровых и
т.п.) и арматуру, сосредоточенную у сжатой и у растянутой грани, должен
производиться в зависимости от положения границы сжатой зоны: а) если граница сжатой зоны
проходит в полке (рис. 5,а), т.е. соблюдается условие RаFа ≤ Rпрb'пh'п + Rа.сF'а, (27) расчет производится как для
прямоугольного сечения шириной b'п в соответствии с указаниями
пп. 3.16
и 3.18; б) если граница сжатой зоны
проходит в ребре (рис. 5,б), т.е. условие (27) не соблюдается,
расчет производится из условия M ≤ Rпрbx(h0 - 0,5x) + Rпр(b'п - b)h'п(h0 - 0,5h'п) + Rа.сF'а(h0 - a'). (28) При этом высота сжатой зоны
бетона x определяется по
формуле и принимается не более ξRh0 (см. табл. 17). Если x
> ξRh0, условие (28)
можно записать в виде M ≤ ARRпрbh02 + Rпр(b'п -
b)h'п(h0 - 0,5h'п) + Rа.сF'а(h0 - a'), (30) где AR - см. табл. 17 п. 3.15. При этом следует учитывать
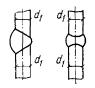
указания п. 3.17. Рис. 5. Форма сжатой зоны в
поперечном сечении таврового железобетонного элемента а -
при расположении границы сжатой зоны в полке; б - при расположении границы сжатой зоны в ребре Примечания:
1. При переменной высоте свесов полки допускается принимать значение h'п равным средней высоте свесов. 2. Ширина сжатой полки b'п, вводимая в расчет, не должна превышать
величины, указанной в п. 3.24. 3.22. Требуемая площадь сечения сжатой арматуры при ξRh0 > h'п определяется по формуле
где AR - см. табл. 17 п. 3.15. 3.23. Требуемая площадь сечения растянутой арматуры определяется следующим
образом: а) если граница сжатой зоны
проходит в полке, т.е. соблюдается условие M ≤ Rпрb'пh'п(h0 - 0,5h'п) + Rа.сF'а(h0 - a'), (32) площадь сечения растянутой арматуры определяется как
для прямоугольного сечения шириной b'п в соответствии с указаниями
пп. 3.19
и 3.20
[по формуле (26)]; б) если граница сжатой зоны
проходит в ребре, т.е. условие (32) не соблюдается, площадь сечения растянутой
арматуры определяется по формуле где ξ определяется по табл. 18 в
зависимости от значения
При этом должно
удовлетворяться условие A0 ≤ AR (см. табл. 17). 3.24(3.16). Вводимая в расчет ширина сжатой полки b'п принимается из условия, что ширина свеса в каждую сторону от ребра должна быть не более 1/6
пролета элемента и не более: а) при наличии поперечных
ребер или при h'п ≥ 0,1h - 1/2
расстояния в свету между продольными ребрами; б) при
отсутствии поперечных ребер (или при расстояниях между ними, больших чем
расстояния между продольными ребрами) и h'п < 0,1h - 6h'п; в) при
консольных свесах полки: при h'п ≥ 0,1h - 6h'п; при 0,05h
≤ h'п < 0,1h - 3h'п; при h'п < 0,05h - свесы не учитываются. Примеры
расчета
Прямоугольные
сечения Пример
1. Дано:
размеры сечения b = 30 см; h = 60 см; a = 4 см; mб1 = 0,85 (нагрузки малой
суммарной длительности отсутствуют); расчетный изгибающий момент M = 20
тс·м; бетон марки М 200 (Rпр = 75 кгс/см2);
арматура класса А-II (Rа = 2700 кгс/см2). Требуется определить площадь
сечения продольной арматуры. Расчет. h0 = 60 - 4 = 56 см. Подбор
продольной арматуры производим согласно п. 3.19. По формуле (22)
вычисляем значение A0:
Из табл. 17 для
элемента из бетона марки М 200 с арматурой класса А-II при mб1 =
0,85 находим AR = 0,451. Так как A0 = 0,284 < AR = 0,451, то сжатой арматуры по расчету не требуется. Из табл. 18 при A0 = 0,284 находим υ =
0,829. Требуемую площадь сечения
растянутой арматуры определяем из формулы (23):
Принимаем 3Æ28 (Fа = 18,47 см2). Пример
2. Дано:
размеры сечения b = 30 см; h =
80 см; a
= 7 см; растянутая арматура класса А-III (Rа = 3400 кгс/см2) с
площадью поперечного сечения Fа =
29,45 см2
(6Æ25); mб1 = 0,85 (нагрузки с малой
суммарной длительностью отсутствуют); бетон марки М 300 (Rпр = 115 кгс/см2);
расчетный изгибающий момент M = 55 тс·м. Требуется проверить прочность
сечения. Расчет. h0 = 80 - 7 = 73 см. Проверку
прочности сечения производим согласно п. 3.18. Определяем значение x:
Из табл. 17 для
элементов из бетона марки М 300 с арматурой класса А-III при mб1 = 0,85 находим ξR = 0,625. Так как ξ = x/h0 = 29/73 = 0,397 < ξR = 0,625, прочность проверяем
из условия (20): RаFа(h0 -
0,5x) = 3400·29,45(73 - 0,5·29) = 5850000 кгс·см = 58,5
тс·м > M = 55 тс·м, т.е. прочность сечения обеспечена. Пример
3. Дано: размеры сечения b = 30 см; h = 80 см; a = 5
см; арматура класса А-III (Rа =
Rа.с = 3400 кгс/см2); расчетный изгибающий
момент с учетом крановой нагрузки MII = 78 тс·м, а момент без учета крановой нагрузки MI =
63 тс·м; бетон марки М 200 (Rпр = 90 кгс/см2 при mб1 = 1). Требуется определить площадь
сечения продольной арматуры. Расчет. Расчет ведем на полную
нагрузку, корректируя расчетное сопротивление бетона согласно п. 3.1. Так как mб.д = 0,85MII/MI =
0,85·78/63 = 1,05 < 1,1, то принимаем Rпр = 90·1,05 = 94,5 кгс/см2, h0 = 80 - 5 = 75 см. Определяем требуемую площадь
продольной арматуры согласно п. 3.19. По формуле (22) находим величину
Так как A0 = 0,49 > AR = 0,429 (см. табл. 17 при mб1 = 1), то при заданных
размерах сечения и марке бетона необходима сжатая арматура. Далее расчет ведем
согласно указаниям п. 3.20. Принимая величину a' = 3
см, по формулам (24) и (25) определяем необходимую
площадь сечения сжатой и растянутой арматуры:
Принимаем F'а = 6,03 см2 (3Æ16); Fа = 40,21 см2 (5Æ32). Пример
4. Дано:
размеры сечения b = 30 см; h = 70 см; a = 5 см; a' = 3
см; бетон марки М 400 (Rпр = 150 кгс/см2 при
mб1 = 0,85); арматура класса А-III (Rа =
Rа.с = 3400 кгс/см2); площадь сечения сжатой арматуры F'а = 9,42 см2 (3Æ20); расчетный изгибающий момент M = 58 тс·м. Требуется определить площадь
сечения растянутой арматуры. Расчет. h0 = 70 - 5 = 65 см. Расчет ведем с
учетом площади сжатой арматуры согласно указаниям п. 3.20. Вычисляем значение A0:
A0 = 0,201 < AR = 0,417 (см. табл. 17). По табл. 18 при A0 = 0,201 находим ξ =
0,23. Необходимую площадь
растянутой арматуры определяем по формуле (26): Fа =
ξbh0Rпр/Rа +
F'а = 0,23·30·65·150/3400 + 9,42 = 29,22 см2. Принимаем 3Æ36 (Fа = 30,34 см2). Пример
5. Дано:
размеры сечения b = 30 см; h = 70 см; a = 7 см; бетон марки М 300 (Rпр = 115 кгс/см2 при
mб1 = 0,85); арматура класса А-III (Rа =
Rа.с = 3400 кгс/см2); площадь сечения растянутой арматуры Fа = 48,26 см2 (6Æ32); сжатой арматуры F'а =
3,39 см2
(3Æ12); расчетный изгибающий
момент M = 60 тс·м. Требуется проверить прочность
сечения. Расчет. h0 = 70 - 7 = 63 см. Проверку прочности сечения
производим согласно п. 3.16. По формуле (16)
вычисляем высоту сжатой зоны:
По табл. 17
находим ξR = 0,625; AR = 0,43. Так как x =
44,2 см > ξRh0 = 0,625·63 = 39,4 см, то
прочность сечения проверяем из условия (18): ARRпрbh02 + Rа.сF'а(h0 - a') = 0,43·115·30·632
+ 3400·3,39(63 - 3) = 65,8 тс·м > M =
60 тс·м, т.е. прочность сечения обеспечена. Тавровые и
двутавровые сечения Пример
6. Дано:
размеры сечения b'п = 150 см; h'п = 5 см; b = 20 см; h = 40 см; a = 4 см; mб1 = 0,85 (нагрузки малой
суммарной длительности отсутствуют); бетон марки М 300 (Rпр = 115 кгс/см2);
арматура класса А-III (Rа = 3400 кгс/см2);
расчетный изгибающий момент M = 25 тс·м. Требуется определить площадь
сечения продольной арматуры. Расчет. h0 = 40 - 4 = 36 см. Расчет ведем согласно указаниям п.
3.23
в предположении, что сжатая арматура по расчету не потребуется. Так как Rпрb'пh'п(h0 - 0,5h'п) = 115·150·5(36 - 0,5·5) =
28,9 тс·м > M = 25 тс·м, т.е. граница
сжатой зоны проходит в полке и сжатой арматуры не требуется, расчет производим
как для прямоугольного сечения шириной b'п (см. п. 3.23
«а»). Определяем величину A0 по формуле (22):
Площадь сечения растянутой
арматуры вычисляем по формуле (23). Для этого по табл. 18 при A0 = 0,112 находим υ = 0,94. Тогда
Принимаем 4Æ28 (Fа = 24,63 см2). Пример
7. Дано:
размеры сечения b'п = 40 см; h'п = 12 см; b = 20 см; h =
60 см; a = 6 см; бетон марки М 200 (Rпр = 75 кгс/см2 при mб1 = 0,85); арматура класса А-III (Rа = 3400 кгс/см2); расчетный изгибающий
момент M = 27 тс·м. Требуется определять площадь
сечения растянутой арматуры. Расчет. h0 = 60 - 6 = 54 см. Расчет ведем согласно указаниям п.
3.23
в предположении, что сжатая арматура по расчету не потребуется. Так как Rпрb'пh'п(h0 - 0,5h'п) = 75·40·12(54 - 0,5·12) =
1728000 кгс·см = 17,28 тс·м < M =
27 тс·м, т.е. граница сжатой зоны проходит в ребре, то площадь сечения
растянутой арматуры определяем по формуле (33). Для этого вычисляем значение A0:
(см. табл. 17), следовательно, сжатой
арматуры не требуется. По табл. 18 при A0 = 0,42 находим ξ = 0,6.
Тогда Fа = [ξbh0
+(b'п - b)h'п]Rпр/Rа = [0,6·20·54 + (40 -
20)12]75/3400 = 19,6 см2. Принимаем 4Æ25 (Fа =
19,64 см2). Пример
8. Дано:
размеры сечения b'п = 40 см; h'п = 10 см; b = 20 см; h = 60 см; a = 7 см; бетон марки М 300 (Rпр = 115 кгс/см2 при
mб1 = 0,85); растянутая арматура
класса А-III (Rа = 3400 кгс/см2) с
площадью сечения Fа = 19,64 см2 (4Æ25); F'а = 0; расчетный изгибающий момент M = 25 тс·м. Требуется проверить прочность
сечения. Расчет. h0 = 60 - 7 = 53 см. Проверку прочности сечения производим
согласно п. 3.21. Так как RаFа = 3400·19,64 = 66800 кгс
> Rпр b'пh'п = 115·40·10 = 46000 кгс, то граница сжатой зоны проходит в ребре, и прочность
сечения проверяем из условия (28). Для этого по формуле (29)
определяем высоту сжатой зоны x:
Rпрbx(h0
- 0,5x) + Rпр(b'п - b)h'п(h0 - 0,5h'п) = 115·20·19(53 -
0,5·19) + 115(40 - 20)10(53 - 0,5·10) = 3050000 кгс·см = 30
тс·м > M = 25 тс·м, т.е. прочность сечения обеспечена. Элементы, работающие на косой изгиб
3.25. Расчет прямоугольных, тавровых, двутавровых и Г-образных сечений
элементов, работающих на косой изгиб, допускается производить, принимая форму
сжатой зоны по рис. 6, при этом должно удовлетворяться условие Mх ≤ Rпр[Sсв.х + Fреб(h0 - x/3)] + Rа.сSа.х, (35) Рис. 6. Форма сжатой зоны в
поперечном сечении железобетонного элемента, работающего на косой изгиб а -
таврового сечения; б -
прямоугольного сечения; 1 - плоскость
действия изгибающего момента; 2 - центр тяжести сечения растянутой
арматуры Рис. 7. Сечение с растянутыми
арматурными стержнями в плоскости оси x 1 - плоскость действия изгибающего момента где Mх - составляющая изгибающего момента в плоскости оси x (за оси x и y принимаются две взаимно перпендикулярные оси, проходящие через
центр тяжести сечения растянутой арматуры, параллельно сторонам сечения; для
сечения с полкой ось x принимается
параллельно плоскости ребра); Fреб = Fб - Fсв; (36) Fб - площадь сжатой зоны бетона, равная Fсв -
площадь наиболее сжатого свеса полки; x - размер сжатой зоны бетона по наиболее сжатой
боковой стороне сечения, определяемый по формуле Sсв.х - статический момент площади Fсв в плоскости оси x относительно оси y; Sсв.у - то же, в плоскости оси y относительно оси x; b0 - расстояние от центра тяжести сечения растянутой
арматуры до наиболее сжатой боковой грани ребра (стороны); Sа.х - статический момент площади сечения сжатой арматуры
в плоскости оси x относительно
оси y; Sа.у - то же, в плоскости оси y относительно оси x; Mу - составляющая изгибающего
момента в плоскости оси y. Если растянутые арматурные
стержни располагаются в плоскости оси x (рис. 7), значение x вычисляют только по формуле где
β - угол
наклона плоскости действия изгибающего момента к оси x, т.е. ctgβ = Mх/Mу. Формулой (39)
также следует пользоваться независимо от расположения арматуры, если необходимо
определить предельное значение изгибающего момента при заданном угле β. При расчете прямоугольных
сечений значения Fсв, Sсв.х и Sсв.у в формулах (35), (36), (38) и (39)
принимаются равными нулю. Если Fб < Fсв или если x < 0,2h'п, расчет производится как для
прямоугольного сечения шириной b =
b'п. Если выполняется условие где bсв - ширина наименее сжатого
свеса полки, то расчет производится без учета косого изгиба, т.е. по формулам
пп. 3.16
- 3.24
на действие момента M = Mх; при этом следует проверить
условие (41),
принимая x = 1,5Fреб/(b + bсв). При определении значения Fб по формуле (37)
напряжение в растянутом стержне, ближайшем к границе сжатой зоны, не должно
быть меньше Rа, что обеспечивается
соблюдением условия где ξR - см. табл. 17 п. 3.15; b0i и h0i - расстояние от рассматриваемого стержня
соответственно до наиболее сжатой боковой грани ребра (стороны) и до наиболее
сжатой грани, нормальной к оси x
(см. рис. 6); bсв - ширина наиболее сжатого свеса; γ - угол
наклона прямой, ограничивающей сжатую зону, к оси y; значение tgγ определяется по формуле
Если условие (41) не
соблюдается, расчет сечения следует производить последовательными
приближениями, заменяя в формуле (37) для каждого растянутого стержня величину Rа значениями напряжений,
равными σаi = s(ξ0/ξi - 1)Rа, но не более Rа, где s и ξ0 - см. табл. 17; при
этом уточняют положение осей x и
y, проводя их через
точку приложения равнодействующей усилий в растянутых стержнях. При проектировании
конструкций не рекомендуется допускать превышение значений ξi над ξR более чем на 20 %. При
выполнении этой рекомендации допускается производить только один повторный расчет
с заменой в формуле (37) значений Rа для растянутых стержней, где ξi > ξR, на напряжения, равные При повторном расчете
значение x определяется
по формуле (39)
независимо от расположения растянутых стержней. Если выполняются условия: для
прямоугольных и тавровых сечений с полкой в сжатой зоне x
> h, (43) для двутавровых и тавровых
сечений с полкой в растянутой зоне x > h - hп - bсв.рtgγ (44) (где hп и bсв.р - высота и ширина наименее
растянутого свеса полки, см. рис. 8), то расчет на косой изгиб производится согласно
п. 3.28. При использовании формул
настоящего пункта за растянутую арматуру площадью Fа допускается принимать
арматуру, располагаемую вблизи растянутой грани, параллельной оси y, а за сжатую арматуру площадью F'а - арматуру, располагаемую
вблизи сжатой грани, параллельной оси y, но по одну, наиболее сжатую сторону от оси x (см. рис. 6). Рис. 8. Тавровое сечение со
сжатой зоной, заходящей в наименее растянутый свес полки 1 - плоскость действия изгибающего момента 3.26. Определение требуемого количества растянутой арматуры при косом изгибе
для элементов прямоугольного, таврового и Г-образного сечения с полкой в сжатой
зоне может производиться при помощи графика на рис. 9. Для этого ориентировочно
задаются положением центра тяжести сечения растянутой арматуры. Затем по
графику определяют величину α в зависимости от значений:
и
(обозначения см. в п. 3.25). Рис. 9. График несущей
способности прямоугольного, таврового и Г-образного сечения для элементов,
работающих на косой изгиб Если значение mх меньше нуля, расчет следует производить как для прямоугольного
сечения, принимая b =
b'п. Если значение α на
графике находится по левую сторону от кривой, отвечающей параметру Требуемая площадь растянутой
арматуры при условии работы ее с полным расчетным сопротивлением определяется
по формуле Fа = (αb0h0 + Fсв)Rпр/Rа + F'аRа.с/Rа, (45) где Fсв - см. п. 3.25. Центр тяжести сечения
фактически принятой растянутой арматуры должен отстоять от растянутых граней не
дальше принятого в расчете центра тяжести. В противном случае расчет повторяют,
принимая новый центр тяжести сечения растянутой арматуры. Условием работы растянутой
арматуры с полным расчетным сопротивлением является удовлетворение условия (41) п. 3.25. Для элементов из бетона марки
М 300 и ниже условие (41) всегда удовлетворяется, если значение α на
графике рис. 9
находится внутри области, ограниченной осями координат и кривой отвечающей
параметру b'св/b0. Если условие (41) не
удовлетворяется, следует поставить (увеличить) сжатую арматуру либо повысить
марку бетона, либо увеличить размеры сечения (в особенности размеры наиболее
сжатого свеса). Значения α на
графике не должны находиться между осью mу и кривой, отвечающей
параметру h0/h. В противном случае x становится больше h, и расчет тогда производится согласно п. 3.28. 3.27. Расчет на косой изгиб прямоугольных и двутавровых симметричных сечений
с симметрично расположенной арматурой можно производить согласно пп. 3.76 - 3.77, принимая N = 0. 3.28. Для не оговоренных в пп. 3.25 - 3.27 сечений, а также при выполнении
условий (43) и (44) п. 3.25 или, если арматура распределена по сечению, что не позволяет до расчета
установить значения Fа и F'а и
расположение центров тяжести растянутой и сжатой арматуры, расчет на косой
изгиб следует производить, пользуясь формулами для общего случая расчета
нормального сечения (п. 3.78) с учетом указаний п. 3.14. Рекомендуется пользоваться
формулами общего случая в следующем порядке: 1) проводят две взаимно
перпендикулярные оси x и
y через центр тяжести
сечения наиболее растянутого стержня по возможности параллельно сторонам
сечения; 2) подбирают
последовательными приближениями положение прямой, ограничивающей сжатую зону,
так, чтобы при N = 0 удовлетворилось равенство (138) после подстановки в
него значений σаi,
определенных по формуле (139). При этом угол наклона этой прямой γ
принимают постоянным и равным углу наклона нейтральной оси, определенному как
для упругого материала; 3) определяют моменты
внутренних усилий относительно осей x и y соответственно Mу.пр
и Mх.пр; 4) если
оба эти момента оказываются больше или меньше соответствующих составляющих
внешнего момента Mу и Mх, то прочность
сечения считается соответственно обеспеченной или не обеспеченной. Если один из этих моментов
(например, Mу.пр) меньше соответствующей составляющей внешнего
момента (Mу), а другой момент больше составляющей внешнего момента (т.е. Mх.пр > Mх), то задаются другим углом γ
(большим, чем ранее принятый) и снова производят аналогичный расчет. Примеры
расчета элементов, работающих на косой изгиб
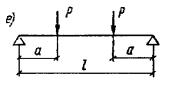
Пример 9. Дано: железобетонный прогон кровли с уклоном 1:4 (ctgβ = 4); сечение и расположение
арматуры - по рис. 10; mб1 = 0,85 (нагрузки малой
суммарной длительности отсутствуют); бетон марки М 300 (Rпр = 115 кгс/см2); растянутая арматура класса А-III (Rа = 3400 кгс/см2);
площадь сечения Fа = 7,63 см2 (3Æ18); расчетный изгибающий момент в вертикальной плоскости M = 7,42 тс·м. Требуется проверить прочность
сечения. Расчет. Из рис. 10
следует: h0 = 40 - 3 - 1·3/3= 36 см; b0 = (2·12 + 1·3)/3 = 9 см; b'св = bсв = (30 - 15)/2 = 7,5 см; h'п = 8 + 2/2 = 9 см. По формуле (37)
определяем площадь сжатой зоны бетона
Площадь наиболее сжатого
свеса полки и статические моменты этой площади относительно осей x и y соответственно равны: Fсв = b'св·h'п = 7,5·9 = 67,5 см2; Sсв.у = Fсв(b0 + b'св/2) = 67,5(9 + 7,5/2) = 861
см3; Sсв.х = Fсв(h0 - h'п/2) = 67,5(36 - 9/2) = 2125
см3. Рис. 10. К примеру 9 1 - плоскость действия изгибающего момента; 2 - центр тяжести сечения растянутой
арматуры Так как Fб > Fсв, то расчет продолжаем как для таврового сечения: Fреб = Fб - Fсв = 225,5 - 67,5 = 158 см2. Составляющие изгибающего
момента в плоскости осей y и
x соответственно равны
(принимая ctgβ = 4):
Mх = Mcosβ = Mуctgβ = 1,8·4 = 7,2 тс·м. Определяем по формуле (38)
высоту сжатой зоны x по
наиболее сжатой стороне сечения:
Проверим условие (40):
Следовательно, расчет
продолжаем по формулам косого изгиба. Проверяем условие (41) для
наименее растянутого стержня. Из рис. 10 имеем b0i = 3 см; h0i = 40 - 3 = 37 см:
Условие (41) не
соблюдается и расчет повторяем, заменяя в формуле (37) значение Rа для наименее растянутого
стержня на напряжение σа, определенное по формуле (42), и
корректируя значения h0 и b0. Из табл. 17 имеем
ξ0 = 0,758 и s = 4,73:
Поскольку все стержни
одинакового диаметра, новые значения Fб, b0 и h0 будут равны: Fб = 225,5(2 + 0,911)/3 = 215,3 см2; b0 = (2·12 + 0,911·3)/(2 +
0,911) = 9,18 см; h0 = 40 - 3 - 1·3/(2 + 0,911) = 35,97 см. Аналогично определяем
значения Sсв.у, Sсв.х, Fреб: Sсв.у = 67,5(9,18 + 7,5/2) = 883 см3; Sсв.х = 76,5(35,97 - 9/2) = 2125
см3; Fреб = 215,3 - 67,5 = 147,8 см2. Значение x определяем по формуле (39):
Проверяем прочность сечения
из условия (35): Rпр[Sсв.х + Fреб(h0 - x/3)]
= 115[2125 + 147,8(35,97 - 22,25/3)] = 729000 = 7,29 тс·м > Mх = 7,2 тс·м, т.е. прочность сечения обеспечена. Пример
10. По
данным примера 9
подобрать площадь растянутой арматуры при расчетном моменте в вертикальной
плоскости M = 6,39 тс·м. Расчет. Составляющие изгибающего
момента в плоскости оси x и
оси y равны:
Mх = Mу
ctgβ = 1,55·4 = 6,2 тс·м. Определим необходимое
количество арматуры согласно п. 3.26. Принимая значения b0, h0, Sсв.х и Sсв.у из примера 9, находим значения mх и mу:
Так как mх больше нуля, расчет
продолжаем как для таврового сечения. Поскольку точка с
координатами mх = 0,280 и mу = 0,167 на графике рис. 9 находится по правую сторону от
кривой, отвечающей параметру (bсв + b)/b0
= (7,5 + 15)/9 = 2,5 и по левую сторону от кривой, отвечающей параметру b'св/b0
= 7,5/9 = 0,83, арматура будет работать с полным расчетным сопротивлением, т.е.
условие (41)
удовлетворяется, и требуемую площадь арматуры определяем по формуле (45). По графику на рис. 9 при mх = 0,28 и mу = 0,167 находим α = 0,33. Тогда Fа
= (αb0h0 + Fсв)Rпр/Rа = (0,33·9·36 + 67,5)115/3400 = 5,9 см2. Принимаем стержни 3Æ16 (Fа = 6,03 см2) и
располагаем их так, как показано на рис. 10. Расчет сечений,
наклонных к продольной оси элемента
3.29(3.29). Расчет по прочности сечений, наклонных к продольной оси элемента,
должен производиться: на действие поперечной силы (см. пп. 3.30 - 3.44); на действие изгибающего
момента (см. пп. 3.45 - 3.50). Общие положения расчета наклонных сечений на
действие поперечной силы
3.30(3.30). При расчете элементов на действие поперечной силы должно соблюдаться
условие Q ≤ 0,35Rпрbh0, (46) при этом значение Rпр для бетонов проектных марок
выше М 400 принимается как для бетона марки М 400. При переменной ширине b по высоте элемента в расчет [в
формулу (46)
и последующие] вводится ширина элемента на уровне середины высоты сечения (без
учета полок). 3.31(3.31). Расчет на действие поперечной силы, согласно указаниям пп. 3.32 - 3.44, не производится, если
соблюдается условие Q ≤ k1Rрbh0, (47) где k1 - коэффициент, принимаемый
равным: для линейных элементов
(балок, ребер и т.п.) - 0,6; для сплошных плоских плит - 0,75. При соблюдении условия (47)
поперечная арматура определяется конструктивными требованиями (см. пп. 5.72 - 5.74). Примечание.
В тексте настоящего Руководства под поперечной арматурой имеются в виду хомуты
и отогнутые стержни. Термин «хомуты» включает поперечные стержни сварных
каркасов и хомуты вязаных каркасов, выполненные в соответствии с указаниями пп.
5.72
- 5.74. 3.32(3.33). Расчет элементов постоянного сечения с поперечной арматурой (рис. 11) должен производиться из
условия Q ≤ ΣRа.хFх + ΣRа.хFоsinα + Qб, (48) где Q - поперечная сила, действующая в наклонном сечении, т.е.
равнодействующая всех поперечных аил от внешней нагрузки, расположенных по одну
сторону от рассматриваемого наклонного сечения (см. рис. 12); при
этом, если не имеет место случай, оговоренный в п. 3.34, следует учитывать
вероятность отсутствия нагрузки в пределах наклонного сечения, т.е. принимать
значение Q равным максимальной
поперечной силе в пределах наклонного сечения; ΣRа.хFх и ΣRа.хFоsinα - сумма
поперечных усилий, воспринимаемых соответственно хомутами и отогнутыми
стержнями, пересекающими наклонное сечение; α - угол наклона отогнутых
стержней к продольной оси элемента в наклонном сечении; Qб - поперечное усилие, воспринимаемое бетоном сжатой зоны в наклоняем
сечении. Величина Qб определяется по формуле
здесь c - длина
проекции наклонного сечения на продольную ось элемента. Рис. 11. Схема усилий,
действующих в наклонном сечении изгибаемого элемента с поперечной арматурой,
при расчете по поперечной силе Рис. 12. Определение расчетного
значения поперечной силы 3.33(3.35). Для хомутов, устанавливаемых по расчету, в элементе с поперечной
нагрузкой в пределах его пролета должно удовлетворяться условие При этом, если выполняются
указания пп. 3.42
и 3.43,
условие (50)
можно не проверять. Расстояния между хомутами u, между опорой и концом отгиба, ближайшего к опоре, u1, а также между концом
предыдущего и началом последующего отгиба u2 (рис. 14) должны быть не более величины Кроме того, поперечное
армирование элемента независимо от результатов расчета должно удовлетворять
конструктивным требованиям, приведенным в пп. 5.72 - 5.74. 3.34. В элементах, рассчитываемых только на фиксированные нагрузки, в том
числе на сплошные распределенные нагрузки (например, гидростатическое
давление), расчетную поперечную силу Q следует определять с учетом разгружающего влияния нагрузки, приложенной
к элементу в пределах длины проекции наклонного сечения, если эта нагрузка
приложена по грани элемента и действует в его сторону (например, в
горизонтальном элементе - нагрузка, действующая сверху вниз и приложенная к
верхней грани). Расчет элементов, армированных хомутами без
отогнутых стержней
3.35. Проверка прочности по поперечной силе производится для невыгоднейших
сечений, начинающихся у опоры и в местах изменения интенсивности хомутов (рис. 13), из условия Q ≤ Qх.б (52) где Q - поперечная сила в нормальном сечении у начала рассматриваемого
наклонного сечения (у опоры и в местах изменения интенсивности поперечного
армирования); Qх.б - предельная поперечная сила, воспринимаемая бетоном и хомутами в
невыгоднейшем наклонном сечении, определяемая по формуле здесь qх - усилие в хомутах на единицу
длины элемента в пределах наклонного сечения, определяемое по формуле При этом длина проекции
невыгоднейшего наклонного сечения определяется по формуле 3.36. Определение требуемой
интенсивности хомутов производится из формулы где Q и qх - см. п. 3.35. 3.37. При расчете элемента на действие равномерно распределенной нагрузки p, приложенной
по грани элемента и действующей в его сторону, допускается в формулы (53), (55) и (56) вместо величины qх подставлять
величину (qх + p1), где значение p1 определяется
следующим образом: а) если нагрузка на отдельных
участках пролета может отсутствовать и эпюра M от
принятой в расчете равномерно распределенной нагрузки p всегда огибает любую действительную эпюру M (например, нагрузка на перекрытия) - p1 =
p/2; б) если равномерно распределенная нагрузка фиксированная и
сплошная (например, гидростатическое давление) - p1 =
p, при этом собственный вес, входящий в нагрузку p1, учитывается в ней с
коэффициентом 0,5. в) в прочих случаях - p1 = 0. Рис. 13. Места расположения
невыгоднейших наклонных сечений при расчете по поперечной силе и определение места
изменения интенсивности хомутов 1 и 2 - невыгоднейшие наклонные сечения При действии фиксированной
сосредоточенной силы Pi, приложенной к верхней грани элемента в пределах невыгоднейшего
наклонного сечения с длиной проекции c0 (см. п. 3.35),
допускается расчет из условия (52) производить на действие поперечной силы,
равной Q - Pi; при этом следует проверить
также условие где ci - длина проекции наклонного сечения, направленного к точке приложения
сосредоточенной силы Pi. 3.38. При изменении интенсивности хомутов по длине элемента с qх1 на qх2 (например, увеличением шага хомутов) участок с интенсивностью qх1 принимается до сечения, в котором поперечная сила Q становится равной усилию Qх.б2, воспринимаемого бетоном и хомутами при интенсивности хомутов qх2 (см. рис. 13). При наличии равномерно распределенной нагрузки длина участка с интенсивностью
qх1 принимается не менее где Q - наибольшая поперечная сила на участке l1 (у опоры); p и Pi - равномерно
распределенная и сосредоточенная нагрузки, действующие в пределах длины l1. Если интенсивность хомутов qх2 не удовлетворяет условию (50) п. 3.33,
т.е. они поставлены по конструктивным соображениям участок с интенсивностью qх1 принимается до сечения, в
котором поперечная сила Q становится равной Q1 = k1Rрbh0, (где k1 - см. п. 3.31). В
этом случае значение l1 определяется по формуле (58) с
заменой Qх.б2 на Q1. Длина участка с интенсивностью
qх1 должна также приниматься не
менее
Кроме того, следует учитывать
конструктивные требования п. 5.73. Расчет элементов с отогнутыми стержнями
3.39. Проверка прочности по
поперечной силе производился для невыгоднейших наклонных сечений, начинающихся
у опоры и у начала отогнутых стержней (рис. 14), из условия Q
≤ Qх.б + Rа.хFоsinα, (60) где Q - поперечная сила в нормальном сечении у начала рассматриваемого
сечения (у опоры и у начала отгибов); Fо - площадь сечения отогнутых стержней в ближайшей за началом
рассматриваемого наклонного сечения плоскости отгиба; α - угол наклона плоскости
отогнутых стержней к оси элемента; Qх.б - см.
п. 3.35. При наличии фиксированных
сосредоточенных или равномерно распределенных нагрузок допускается учитывать
указания п. 3.37. Рис. 14. Места расположения
невыгоднейших наклонных сечений при расчете по поперечной силе для элементов с
отогнутыми стержнями 1, 2 и 3 - невыгоднейшие наклонные сечения 3.40. Необходимое сечение отогнутых стержней, расположенных в одной
плоскости, определяется из условия
При этом поперечная сила Q принимается: а) при расчете отогнутых
стержней первой (от опоры) плоскости - равной поперечной силе у опоры; б) при расчете отогнутых
стержней каждой из последующих плоскостей - равной поперечной силе у начала
предыдущей (по отношению к опоре) плоскости отогнутых стержней (см. рис. 14). Начало наиболее удаленного от
опоры отгиба должно располагаться не ближе к опоре, чем то сечение, в котором
поперечная сила Q становится больше усилия,
воспринимаемого бетоном и хомутами Qх.б. Кроме того, расположение
отгибов должно удовлетворять требованиям п. 5.75. 3.41. В сплошных плитах с поперечной арматурой только в виде отогнутых
стержней расчет по поперечной силе в общем случае производится из условия (48) при ΣFхRа.х = 0. При действии фиксированных
сосредоточенных сил проверка условия (48) производится для наклонных
сечений, начинающихся в растянутой зоне у опоры и у начала отгибов и
заканчивающихся в сжатой зоне в конце отгибов каждой плоскости, а также в
местах приложения сосредоточенных сил (рис. 15). При расчете плиты на действие
равномерно распределенной нагрузки p условие
(48)
можно заменить условием Q ≤ Qб.р + Rа.хFоsinα, (62) здесь поперечная сила Q определяется согласно п. 3.40, а значение Qб.р определяется по формуле
и принимается не менее 0,75Rрbh0 + 2,67p1h0. Значение p1 принимается согласно
указаниям п. 3.37. Рис. 15. Расположение
невыгоднейших наклонных сечений в плитах с поперечной арматурой только в виде
отогнутых стержней При отсутствии хомутов начало
наиболее удаленного от опоры отгиба должно располагаться не ближе к опоре, чем
то сечение, начиная с которого наклонные сечения будут удовлетворять условиям
п. 3.42. Расчет элементов без поперечной арматуры
3.42(3.36).
Расчет изгибаемых элементов постоянного
сечения без поперечной арматуры (см. п. 5.70) производится из условий: а) Qмакс ≤ k2Rрbh0, (64) где Qмакс - максимальная поперечная
сила у грани опоры; где c - длина проекции наклонного сечения,
проходящего через опору (значение c принимается не более 2h0); Q - поперечная сила в конце рассматриваемого
наклонного сечения. k2 и k3 - коэффициенты, принимаемые равными: для оплошных плоских плит - k2 = 2,5 и k3 = 1,5; для балок, ребер,
многопустотных настилов - k2 =
2 и k3 = 1,2. При проверке условия (65) в
общем случае задаются рядом значений c, равных или меньших 2h0. При действии фиксированных
сосредоточенных сил проверка условия (65) производится для наклонных
сечений, направленных к точкам приложения сосредоточенных сил (рис. 16). При расчете элемента на
действие равномерно распределенной нагрузки p условие (65) можно заменить условием в котором правая часть принимается не менее k1Rрbh0 + 2p1h0, где p1 - см. п. 3.37; k1 - см. п. 3.31; Qмакс - поперечная сила в начале рассматриваемого наклонного сечения. Рис. 16. Расположение
невыгоднейших наклонных сечений в элементах без поперечной арматуры 1 - наклонное сечение, проверяемое на действие
поперечной силы Q1; 2 - наклонное сечение, проверяемое на действие силы Q2 При действии фиксированной и
сплошной нагрузки с линейно-убывающей от опоры интенсивностью также можно
вместо условия (65) использовать условие (66), принимая за
значение p1 среднюю нагрузку на
приопорном участке длиной 2h0, но не более четверти
пролета балки или половины вылета консоли. Если оплошная нагрузка
линейно возрастает от опоры, начиная с нулевой интенсивности, то прочность
проверяется из условия
в котором правая часть принимается не менее k1Rрbh0 + 2mh0, здесь m - изменение интенсивности нагрузки на единице длины
элемента. 3.43. Расчет элементов без поперечной арматуры с переменной высотой сечения
следует производить из условия (64), принимая значение h0 в опорном сечении, и из
условия (65), принимая среднее значение h0 в пределах наклонного
сечения. Для сплошных плит с высотой
сечения, увеличивающейся с увеличением поперечной силы, при действии сплошной
фиксированной равномерно распределенной нагрузки p условие
(65)
можно заменить условием Qмакс ≤ Qб.р, (68) где
но не менее
A = 1,5Rрbh0tgβ; здесь h0 -
рабочая высота плиты в опорном сечении; β - угол между сжатой и растянутой гранями. При линейно-убывающей от
опоры сплошной нагрузке также можно использовать условие (68),
принимая за значение p среднюю нагрузку на при опорном участке длиной Расчет наклонных сечений по поперечной силе
при косом изгибе
3.44. Расчет по поперечной силе элементов прямоугольного сечения,
подвергающихся косому изгибу, производится из условия
где Qх и Qу - составляющие поперечной силы, действующие соответственно в
плоскости симметрии x и в
нормальной к ней плоскости y; Qх.б(х) и Qх.б(у) - предельные поперечные силы, которые могут быть восприняты
наклонным сечением при действии их соответственно только в плоскости x и только в плоскости y, определяемые по формулам:
здесь bх и bу - размеры сечения в направлении, нормальном
соответственно осям x и y; h0х и h0у - рабочие высоты сечения в направлении соответственно
осей x и y; qх(х) и qх(у) - предельные усилия в поперечных стержнях
соответственно в направлении осей x и y на
единицу длины элемента (см. п. 3.35). Примечание.
Отогнутые стержни при расчете на поперечную силу при косом изгибе не
учитываются. Расчет наклонных сечений на
действие изгибающего момента
3.45(3.39). Расчет сечений, наклонных к продольной оси элемента, на действие
изгибающего момента (рис. 17) должен производиться из условия M
≤ RаFаz + ΣRаFozо + ΣRаFхzх, (70) где M - момент всех внешних сил,
расположенных по одну сторону от рассматриваемого наклонного сечения,
относительно оси, проходящей через точку приложения равнодействующей усилий в
сжатой зоне и перпендикулярной к плоскости действия момента; если внешняя
нагрузка приложена к грани свободно опертой балки и действует в ее сторону, то M - изгибающий момент в нормальном
сечении, проходящем через вышеуказанную ось; RаFаz; ΣRаFоzо и ΣRаFхzх - сумма моментов относительно той же оси
соответственно от усилий в продольной арматуре, в отогнутых стержнях и в
хомутах, пересекающих растянутую зону наклонного сечения; z, zо и zх - расстояния от плоскостей расположения соответственно продольной
арматуры, отгибов и хомутов до указанной выше оси. Высота сжатой зоны наклонного
сечения, измеренная по нормали к продольной оси элемента, определяется из
условия равновесия проекций усилий в бетоне и арматуре наклонного сечения на
продольную ось элемента согласно указаниям пп. 3.16 и 3.21. При этом в случае наличия
отгибов в элементе в числителе выражений для x добавляются значения ΣRаFоcosα, где α - угол
наклона отгибов к продольной оси элемента. Если x < 2a', допускается
принимать z = h0 - a'. Рис. 17. Схема усилий,
действующих в наклонном сечении, при расчете по изгибающему моменту Nб - равнодействующая усилий в сжатой зоне Рис. 18. Поперечная арматура,
учитываемая при определении длины зоны анкеровки а -
корытообразная сетка; б -
поперечные стержни сварных пространственных каркасов; в - распределительная арматура сварных
сеток; г - хомуты вязаных каркасов; 1
- стержни, учитываемые в расчете Проверка на действие
изгибающего момента не производится для наклонных сечений, пересекающих
растянутую грань элемента на участках, обеспеченных от образования нормальных
трещин, т.е. там, где момент M от внешней нагрузки, на
которую ведется расчет по прочности, меньше или равен моменту трещинообразования
Mт, определяемому по формуле (222) п.
4.3,
принимая в ней значения Rр вместо RрII. 3.46. Если наклонное сечение пересекает в пределах зоны анкеровки продольную
растянутую арматуру, не имеющую анкеров, то при расчете этого сечения по
изгибающему моменту расчетное сопротивление продольной арматуры снижается путем
умножения его на коэффициент условий работы mа3, равный mа3 = lх/lан, (71) где lх - расстояние от
конца арматуры до точки пересечения наклонного сечения с продольной арматурой; lан - длина зоны анкеровки, определяемая следующим образом: а) для крайних свободных опор
длина зоны анкеровки определяется по формуле где mан - коэффициент,
принимаемый равным: для стержней периодического профиля mан = 0,5, для гладких стержней mан = 0,8; μк - объемный
коэффициент поперечного армирования, определяемый: при наличии хомутов,
охватывающих продольную арматуру (рис. 18), - по формуле μк = fх/2au, здесь fх и u - соответственно площадь
хомута и его шаг; a - расстояние от центра
тяжести продольной арматуры до нижней грани элемента; при наличии поперечных сеток,
охватывающих продольную арматуру, - по формуле (88) п. 3.60; во всех случаях значение μк принимается не более 0,06; σб - напряжение сжатия бетона
на опоре, равное σб
= Q/Fоп (Q -
опорная реакция; Fоп - площадь опирания элемента)
и принимаемое не более 0,5Rпр; в случае отсутствия указанных
хомутов или сеток значения μк и σб в формуле (72)
принимаются равными нулю, а значение lан принимается не менее 200 мм; указанные хомуты и сетки распределяются по всей длине
lх; б) для участков на конце
вылета консоли длина зоны анкеровки определяется согласно п. 5.48 как
для арматуры, заделанной в растянутый бетон. 3.47. Наиболее невыгодное наклонное сечение пересекает продольную растянутую
арматуру в нормальном сечении, в котором внешний момент равен моменту
трещинообразования Mт (см. п. 4.3) с заменой RрII на Rр; при этом длина проекции этого наклонного сечения на продольную ось
элемента, измеренная между точками приложения равнодействующих усилий в
растянутой арматуре и в сжатой зоне, определяется для элементов с постоянной
высотой сечения по формуле где Q1 - поперечная сила в нормальном сечении, проходящем через начало
наклонного сечения в растянутой зоне; Pi и p - сосредоточенная и
равномерно распределенная нагрузки, приложенные к верхней грани элемента в
пределах наклонного сечения; qхw - усилие в хомутах на единицу
длины элемента (интенсивность хомутов), равное
α - угол наклона отгибов к продольной оси элемента. Если значение c, определенное с учетом сосредоточенной силы Pi, оказывается меньше расстояния
до этой силы Pi, а определенное без учета силы Pi - больше этого расстояния,
то за значение c следует
принимать расстояние до силы Pi. При расчете консолей и
опорных участков неразрезных балок нагрузки Pi и p не учитываются в формуле (73). В этом случае значение c
принимается не более расстояния от опоры до начала наклонного сечения в
растянутой зоне. При известных значениях c и qх при отсутствии отгибов
условие (70)
п. 3.45
имеет вид M ≤ RаFаz + 0,5qхwc2. (74) Если в пределах длины c хомуты изменяют свою интенсивность,
то при отсутствии отгибов формула (73) и условие (74)
приобретают вид:
M ≤ RаFаz +
0,5qхw2c2 + (qхw1 -
qхw2)l1(c - l1/2), (74а) где qхw1 и qхw2 - интенсивность хомутов соответственно у
начала наклонного сечения в растянутой зоне и у конца наклонного сечения; l1 - длина участка с интенсивностью qхw1 в пределах длины c (рис.
19). 3.48. Проверку наклонных сечений по изгибающему моменту согласно пп. 3.45 - 3.47 для элементов с постоянной
или плавно меняющейся высотой, допускается не производить в следующих случаях: 1) если растянутую продольную
арматуру можно учитывать с полным расчетным сопротивлением, т.е. если на концах
арматуры имеются надежные анкеры (см. п. 5.49) или если при отсутствии
анкеров наклонное сечение пересекает продольную арматуру вне зоны анкеровки
(т.е. при lх > lан), при этом должны выполняться
требования пп. 3.49
и 3.50; Рис. 19. Изменение
интенсивности хомутов в пределах длины проекции наклонного сечения c Рис. 20. Обрыв растянутых
стержней в пролете 2) для крайних свободных опор
балок, если выполняются условие (47) п. 3.31 или указания пп. 3.42 и 3.43. В остальных случаях расчет
наклонных сечений по изгибающему моменту обязателен. При этом, если условие (70) не
удовлетворяется при поперечной арматуре, установленной исходя из расчета
прочности по поперечной силе или из расчета по раскрытию наклонных трещин,
рекомендуется в первую очередь принимать меры по усилению анкеровки продольной
арматуры или усиливать поперечное армирование у начала наклонного сечения в растянутой
зоне. 3.49(3.40). Для обеспечения прочности наклонных сечений на действие изгибающего
момента в элементах постоянной высоты продольные растянутые стержни, обрываемые
в пролете, должны заводиться за точку теоретического обрыва (т.е. за нормальное
сечение, в котором эти стержни перестают требоваться по расчету) (рис. 20) на длину не менее 20d и не менее величины w, определяемой по формуле: где Q - поперечная сила в нормальном
сечении, проходящем через точку теоретического обрыва стержня; α - то же, что в п. 3.32; d - диаметр обрываемого стержня; qхw - см. п. 3.47. Кроме того, должны быть
учтены требования п. 5.48. Для элементов без хомутов,
нагруженных равномерно распределенной сплошной нагрузкой, значение w
принимается равным h0. 3.50. Для обеспечения прочности наклонных сечений на действие изгибающего
момента начало отгиба в растянутой зоне должно отстоять от нормального сечения,
в котором отгибаемый стержень полностью используется по моменту, не менее чем
на h0/2, а конец отгиба должен быть расположен не ближе того
нормального сечения, в котором отгиб не требуется по расчету. Расчет наклонных сечений в подрезках
3.51. Для элементов с резко меняющейся высотой сечения, например для балок
или консолей, имеющих подрезки, производится расчет по поперечной силе для
наклонных сечений, проходящих у опоры консоли, образованной подрезкой (рис. 21), согласно указаниям пп. 3.32 - 3.41; при этом в расчетные
формулы вводится рабочая высота h01 короткой
консоли, образованной подрезкой. Рис. 21. Невыгоднейшие
наклонные сечения в элементе с подрезкой 1 - при расчете по поперечной силе; 2
- при расчете по изгибающему моменту Хомуты, необходимые для
обеспечения прочности наклонного сечения в подрезке, следует устанавливать на
длине не менее l1 = Q1/qх + u за
конец подрезки и не менее w0, определяемой по формуле (76). 3.52. Для элементов с подрезками должен производиться расчет на действие
изгибающего момента в наклонном сечении, проходящем через входящий угол
подрезки (рис. 21), согласно указаниям пп.
3.45 - 3.50. При этом продольная арматура
в короткой консоли, образованной подрезкой, должна быть заведена за конец
подрезки на длину не менее длины lан (см. п. 5.48) и
не менее величины w0, равной где Q1 - поперечная сила в нормальном сечении у конца
подрезки; Fо - площадь сечения отгибов, проходящих через входящий
угол подрезки; Fх1 - площадь сечения дополнительных хомутов, проходящих
у конца подрезки и не учитываемых при определении интенсивности хомутов у
подрезки;
a0 - расстояние от опоры консоли до конца подрезки; d -
диаметр обрываемого стержня. Хомуты и отгибы,
установленные у конца подрезки, должны удовлетворять условию RаFх1 +
RаFоsinα ≥ Q1(1 - h01/h0), (77) где h01 и h0 - рабочая высота соответственно в короткой консоли
подрезки и в элементе вне подрезки. При выполнении условия (77)
расчет на изгиб наклонного сечения, проходящего через входящий угол подрезки,
допускается производить из условия где M - изгибающий момент в нормальном сечении у конца
подрезки; p - равномерно распределенная нагрузка, действующая на
элемент. Расчетное сопротивление
продольной арматуры в короткой консоли, образованной подрезкой, определяется с
учетом указаний п. 3.46. Примеры
расчета
Расчет наклонных
сечений на действие поперечной силы Пример
11. Дано:
железобетонная балка с размерами поперечного сечения b = 10 см; h = 30 см; h0 = 27 см; бетон марки М 200 (Rпр = 75 кгс/см2; Rр = 6,5 кгс/см2, с
учетом mб1 = 0,85); балка армирована
двумя плоскими каркасами, поперечные стержни из арматурной проволоки класса В-I (Rа.х = 2200 кгс/см2),
диаметром 5 мм (Fх = 0,39 см2) с
шагом u = 10 см; поперечная сила на
опоре Q = 5,2 тс. Требуется проверить прочность
наклонных сечений балки по поперечной силе. Расчет. Проверяем условие (46), п. 3.30. 0,35Rпрbh0 = 0,35·75·10·27 = 7090 кгс
> Q = 5200 кгс. Так как 0,6Rрbh0 = 0,6·6,5·10·27 = 1053 кгс
< Q = 5200 кгс, согласно п. 3.31,
проверка прочности наклонных сечений необходима. Кроме того, должны соблюдаться
требования п. 3.33:
Условия u < h/2 и u < 15 см п. 5.73
также удовлетворяются. Прочность наклонного сечения
проверяем из условия (52), п. 3.35.
Согласно формуле (53):
т.е. - прочность наклонного сечения обеспечена. Пример
12. Дано:
железобетонная балка пролетом l = 5,5 м, нагруженная
равномерно распределенной нагрузкой 3,2 тс/м; размеры поперечного сечения b = 20 см; h = 40 см; h0 = 37 см; бетон марки М 200 (Rпр = 75 кгс/см2, Rр = 6,5 кгс/см2, с
учетом mб1 = 0,85); хомуты из арматуры
класса А-I (Rа.х = 1700 кгс/см2);
поперечная сила на опоре Q =
88 тс. Требуется определить диаметр
и шаг хомутов у опоры, а также выяснить, на каком расстоянии от опоры и как
может быть увеличен их шаг. Расчет. Проверяем требование п. 3.30: 0,35Rпрbh0 = 0,35·75·20·37 = 19,4 тс
> Q = 8,8 тс. Так как 0,6Rрbh0 = 0,6·6,5·20·37 = 2880 кгс
< Q, согласно п. 3.31,
поперечную арматуру подбираем из расчета по прочности. Согласно п. 5.73,
шаг u1 у опоры должен быть не более 1/2h = 20 и 15 см, а в пролете 3/4h = 30 и 50 см. Принимаем шаг хомутов у опоры
u1 = 15 см, а в пролете u2 = 2· u1 = 30 см. Максимально допустимый шаг
хомутов у опоры согласно формуле (51) равен
По формуле (56)
определим требуемую интенсивность хомутов приопорного участка:
Так как условие (50) не
удовлетворяется, принимаем
Отсюда
Принимаем в поперечном
сечении два хомута диаметром 6 мм (Fх = 0,57 см2). Интенсивность хомутов в
пролете определим по формуле (54):
Так как интенсивность хомутов
qх2 не удовлетворяет условию (50),
минимальную длину участка с шагом хомутов u1 = 15 см определяем по
формуле (58)
с заменой Qх.б2 на Q1 = 0,6Rрbh0 = 2,88 тс:
Принимаем длину участка с
шагом хомутов u1 = 15 см равной 1,85 м. Пример
13. Дано:
железобетонная балка с размерами поперечного сечения b = 20 см; h = 60 см; h0 = 55 см; бетон марки М 200 (Rпр = 75 кгс/см2, Rр = 6,5 кгс/см2 при
учете mб1 = 0,85); сварные хомуты из
арматуры класса А-III (Rа.х = 2400 кгс/см2);
нагрузка в виде фиксированных сосредоточенных сил (см. рис. 22). Требуется определить диаметр
хомутов, их число в сечении, шаг у опоры и выяснить, на каком расстоянии и как
может быть увеличен их шаг. Расчет. Проверяем условие (46) п. 3.30: 0,35Rпрbh0 = 0,35·75·20·55 = 28900 кгс =
28,9 тс > Qмакс = 21,2 тс. Определим требуемую
интенсивность хомутов исходя из максимальной поперечной силы у опоры Qмакс = 21,2 тс по формуле (56):
Этой интенсивности
соответствует невыгоднейшее наклонное сечение с длиной проекции равной
т.е. в пределах невыгоднейшего сечения действует
сосредоточенная сила P1 = 8 тс. Согласно п. 3.37
требуемую интенсивность хомутов можно уменьшить, определяя ее по формуле (56) при Q = Qмакс - P1 или из условия (57). По формуле (56)
Из условия (57)
Принимаем максимальное
значение qх1 = 135 кгс/см. Определяем шаг хомутов на
приопорном участке, принимая в сечении два хомута диаметром 6 мм (Fх = 0,57 см2):
Принимаем u1 = 10 см. Назначаем шаг хомутов на
участке с меньшей интенсивностью хомутов u2 = 2u1 = 20 см. Так как этот шаг
удовлетворяет требованиям п. 5.73, относящимся к приопорному участку (u2 = 20 см < 50 см и u2 < h/3), длину участка с шагом u1 определяем из условия
обеспечения прочности согласно п. 3.38. Определяем значение qх2:
т.е. меньшая интенсивность хомутов удовлетворяет
условию (50),
и участок с интенсивностью хомутов u1 принимаем до сечения, в котором усилие Q становится меньше усилия Qхб2, равного
Так как значение Qхб2 больше, чем усилие Q = 13200 кгс за первым грузом,
длину участка с шагом хомутов u1 = 10 см принимаем равным расстоянию от опоры до
первого груза, т.е. l1 = c1 = 60 см. Рис. 22. К примеру расчета 13 Рис. 23. К примеру расчета 15 Пример
14. Дано:
балка днища резервуара с размерами поперечного сечения b = 25 см, h = 50 см, h0 = 45 см; бетон марки М 200 (Rпр =
75 кгс/см2, Rр = 6,5 кгс/см2 с
учетом mб1 = 0,85); хомуты из арматуры
класса А-I (Rа.х = 1700 кгс/см2);
поперечная сила на опоре Q =
20 тс; равномерно распределенная нагрузка от давления воды, приложенная к
верхней грани балки, 6 тс/м; нагрузка от собственного веса балки 0,4 тс/м. Требуется определить шаг и
диаметр хомутов. Расчет. Проверяем требование п. 3.30: 0,35Rпрbh0 = 0,35·75·25·45 = 29,5 > Q =20 тс. Так как 0,6Rрbh0 = 0,6·6,5·25·45 = 4390 кгс
< Q, согласно п. 3.31
расчет по прочности наклонных сечений необходим. Согласно п. 5.73,
шаг хомутов u должен быть не более 1/3h и не более 500 мм. Принимаем
шаг хомутов u = 15 см < 1/3h. Необходимую интенсивность хомутов
найдем по формуле (56) с учетом разгружающего влияния сплошной
равномерно распределенной нагрузки (см. п. 3.37). Суммарная сплошная
равномерно распределенная нагрузка с учетом нагрузки от собственного веса балки
равна: p1 = p = 6
+ 0,5·0,4 = 6,2 тс/м = 62 кгс/см. Тогда
Площадь сечения хомутов в
одном нормальном к оси балки сечении равна
Принимаем в поперечном
сечении 2 хомута диаметром 8 мм (Fх = 1,01 см2). Пример
15. Дано:
эпюра расчетных поперечных сил для балки - по рис. 23; размеры поперечного сечения
b = 30 см, h = 60 см, h0 = 56 см; a' = 4
см; бетон марки М 200 (Rр = 6,5 кгс/см2, Rпр = 75 кгс/см2 с
учетом mб1 = 0,85); хомуты диаметром 8 мм из арматуры класса А-I (Rа.х = 1700 кгс/см2), Fх = 1,01 см2, шаг
хомутов u = 15 см; отогнутые стержни
класса А-II (Rа.х = 2150 кгс/см2), угол наклона отгибов к
оси балки α = 45°. Требуется определить площадь
сечения и расположение отгибов из расчета их на прочность по поперечной силе. Расчет. Определяем предельную
поперечную силу Qх.б, которую способны воспринять в
невыгоднейшем наклонном сечении совместно хомуты и бетон, по формуле (53). Для
этого по формуле (54) найдем усилие в хомутах на единицу длины
элемента.
Согласно п. 3.40,
определим необходимое сечение отгибов в первой от опоры плоскости:
Принимаем Fо = 6,28 см2 (2Æ20). Расстояние от опоры до
верхнего конца первого отгиба принимаем равным 5 см (см. п. 5.75).
Тогда поперечная сила в сечении, проходящем через нижний конец первого отгиба,
равна (см. рис. 23): Q2 = 33(290
- 5 - 52)/290 = 26,5 тс. Требуемую площадь сечения
отогнутой арматуры во второй от оси опоры плоскости отгибов найдем по формуле
Принимаем Fо2 = 2,26 см2 (2Æ12). Согласно п. 3.33,
расстояние между верхним концом второго и нижним концом первого отгиба не
должно превышать
Принимаем это расстояние
равным 34 см. Тогда поперечная сила в сечении, проходящем через нижний конец
второго отгиба, равна (см. рис. 23): Q3 = 33(290
- 5 - 52 - 34 - 52)/290 = 16,6 тс. Так как Q = 16,6 тс < Qх.б = 23,6 тс, то, согласно п. 3.40,
отгибов больше не требуется (при сохранении того же шага хомутов на участке за
вторым отгибом). Пример
16. Дано:
сплошная плита перекрытия пролетом l =
0,5 м и толщиной
h = 5 см,
нагруженная равномерно распределенной нагрузкой p = 7,5 тс/м2;
поперечная арматура отсутствует; a =
1,5 см; бетон марки М 200 (Rр = 6,5 кгс/см2 с
учетом mб1 = 0,85). Требуется проверить прочность
плиты на действие поперечной силы. Расчет. h0 =
h - a = 5 - 1,5 = 3,5 см. Расчет ведем для полосы плиты
шириной b = 100 см. Поперечная сила на опоре
равна Qмакс = pl/2 =
7,5·0,5/2 = 1,875 тс. Проверяем условие (47) п. 3.31,
принимая k1 = 0,75: k1Rрbh0 = 0,75·6,5·100·3,5 = 1707
кгс < Qмакс = 1875 кгс. Следовательно, расчет
прочности необходим. Прочность проверяем согласно
п. 3.42,
принимая k2 = 2,5; k3 =
1,5: k2Rрbh0= 2,5·6,5·100·3,5 = 5690 кгс
> Qмакс, т.е. условие (64)
выполняется. Проверим условие (66). Для
этого вычисляем p1 = p/2 = 7,5/2 = 3,75 тс/м = 37,5
кгс/см:
Так как Qмакс = 1875 кгс < k1Rрbh0 + 2p1h0 = 1970 кгс, то условие (66)
выполнено, и прочность плиты по поперечной силе обеспечена. Пример
17. Дано:
панель резервуара консольного типа с переменной толщиной от 26,2 см в заделке
до 12 см на свободном конце и с вылетом 4,25 м загружена боковым давлением
грунта, учитывающим нагрузку от транспортных средств на поверхности грунта;
давление грунта линейно убывает от 7,06 тс/м2 в заделке до 0,71 тс/м2
на свободном конце; a =
2,2 см; бетон марки М 200 (Rр = 8,5 кгс/см2 при mб1 = 1,1). Требуется проверить прочность
панели по поперечной силе. Расчет. Рабочая высота сечения
панели в заделке равна h0 = 26,2 - 2,2 = 24 см. Определим tgβ, где β - угол между сжатой и
растянутой гранями tgβ =
(26,2 - 12)/425 = 0,0334. Расчет ведем для полосы
панели шириной b = 100 см. Поперечная сила в
заделке равна Qмакс = (7,06 + 0,71)·4,25/2 = 16,5 тс. Проверяем прочность из
условий (64)
и (68)
п. 3.43: 2,5Rрbh0 = 2,5·8,5·100·24 = 51000 кгс
> Qмакс = 11,8 тс, т.е. условие (64)
выполняется. Определим среднюю нагрузку p на приопорном участке длиной
p =
7,06 - (7,06 - 0,71)0,464/(2·4,25) = 6,72 тс/м = 67,2 кгс/см. Определим значение Qб.р: A = 1,5Rрbh0tgβ = 1,5·8,5·100·24·0,0334 = 1020 кгс;
Принимаем Qб.р = 17,94 тс. Так как Qб.р = 17,94 тс > Qмакс = 16,5 тс, то прочность
панели по поперечной силе обеспечена. Расчет наклонных
сечений на действие изгибающего момента Пример
18. Дано:
железобетонная балка пролетом l =
5,5 м, нагруженная равномерно распределенной нагрузкой p = 3,2 тс/м; конструкция
приопорного участка балки по рис. 24; нагрузки малой суммарной длительности
отсутствуют; бетон марки М 200 (Rпр = 75 кгс/см2, Rр = 6,5 кгс/см2 при
mб1 = 0,85); продольная арматура
без анкеров класса А-III (Rа = 3400 кгс/см2), Fа = 9,82 см2 (2Æ25), F'а = 7,5 см2 (2Æ22); хомуты из арматуры класса А-I (Rа = 2100 кгс/см2), диаметром 6 мм и
шагом u = 15 см. Требуется проверить прочность
наклонного сечения по изгибающему моменту. Расчет. h0 = h - a' =
40 - 4 = 36 см. Поперечная сила на опоре
(опорная реакция) равна Q = pl/2 = 3,2·5,5/2 = 8,8 тс. Рис. 24. К примеру расчета 18 Проверим конструктивное
требование п. 5.50. Поскольку 0,6Rрbh0 = 0,6·6,5·20·36 = 2810 кгс
< Q = 8,8 тс, т.е. условие (47) не
выполняется, то длина заведения арматуры за грань опоры lа должна быть не менее 10d = 10·2,5 = 25 см. Из рис. 24
видно, что lа = lоп - 1 см = 28 - 1 = 27 см >
10d, т.е. требование п. 5.50
выполнено. Так как условие (47) не
выполняется и арматура не имеет анкеров, согласно п. 3.48 расчет по изгибающему
моменту необходим, если расчетное наклонное сечение может пересечь продольную
арматуру в зоне анкеровки. Определяем длину зоны
анкеровки, согласно п. 3.46, учитывая наличие хомутов (Æ6), охватывающих продольную арматуру (fх =
0,283 см2): μк = fх/(2au) =
0,283/(2·4·15) = 0,00236 < 0,06;
mан = 0,5 (как для стержней
периодического профиля). Отсюда
Определяем расположение
начала невыгоднейшего наклонного сечения, т.е. расположение нормального
сечения, в котором M = pll1/2 - pl12/2 = Mт. Поскольку μ = Fа/(bh0) = 9,82/(20·36) ≈ 0,0014 < 0,15, момент трещинообразования Mт определяем, согласно пп. 4.3 и 4.4,
принимая Nус = 0 и Fа =
F'а =
0: Mт = RрWт = Rр·0,292bh2 = 6,5·0,292·20·402
= 60700 кгс·см = 0,607 тс·м. Решая вышеприведенное
квадратное уравнение, находим расстояние l1 от равнодействующей опорной реакции до сечения, в
котором M =
Mт:
Так как l1 = 7 см < 9 см (см. рис. 24),
т.е. искомое нормальное сечение оказалось в пределах площадки опирания,
принимаем начало наклонного сечения по грани опоры. Отсюда l1 = 9 см; lх = lа = 27 см. Поскольку lх
< lан, расчет наклонного сечения по изгибающему моменту
необходим. Коэффициент условий работы продольной арматуры при этом равен mа3 = lх/lан = 27/69,9 = 0,386, а расчетное сопротивление арматуры равно Rа = 3400·0,386 = 1314 кгс/см2. Определяем длину проекции
невыгоднейшего наклонного сечения по формуле (73). Для этого вычисляем: qхw =
RаFх/u = 2100·0,57/15 = 79,7 кгс/см; Q1 = Q -
pl1 = 8,8 - 3,2·0,09 = 8,51 тс. Тогда
Внешний изгибающий момент в
нормальном сечении, проходящем через равнодействующую усилий сжатой зоны
наклонного сечения (т.е. в сечении, расположенном на расстоянии l1 + c = 0,09 + 0,762 = 0,852 м от опорной реакции), равен M =
Q(l1 + c) - p(l1 + c)2/2
= 8,8·0,852 - 3,2·0,8522/2 = 6,34 тс·м. Так как высота сжатой зоны
согласно п. 3.45, принимаем z = h0 - a' = 36 - 3,5 = 32,5 см. Проверяем прочность из
условия (74): RаFаz +
0,5qхwc2 = 1314·9,82·32,5 + 0,5·79,7·76,22 = 651000 кгс·см = 6,51 тс·м > M = 6,34 тс·м, т.е. прочность наклонного сечения по изгибающему
моменту обеспечена. Пример
19. Дано:
ригель многоэтажной рамы с эпюрами изгибающих моментов и поперечных сил от
равномерно распределенной нагрузки p =
22,8 тс/м по рис. 25; бетон марки М 300; продольная и поперечная
арматура класса А-III (Rа = 3400 кгс/см2);
поперечное сечение приопорного участка по рис. 25; хомуты диаметром 10 мм и
шагом 15 см (Fх = 2,36 см2). Требуется определить
расстояние от опоры до места обрыва первого стержня верхней арматуры у левой
опоры. Рис. 25. К примеру расчета 19 Расчет. Определяем предельный
изгибающий момент, растягивающий опорную арматуру без учета обрываемого
стержня, из условия (19), п. 3.16, поскольку Fа = 16,09 см2 > F'а, т.е. x
< 0: Mпр = RаFа(h0 - a') = 3400·16,09(74 - 5) = 37,7
тс·м. По эпюре моментов определяем
расстояние x от опоры до места
теоретического обрыва первого стержня из уравнения M =
Mоп - (Mоп - M'оп)x/l - plx/2 + px2/2
= Mпр, откуда
Поперечная сила в месте
теоретического обрыва Q =
53,2 тс (см. рис. 25). Определяем величину qхw: qхw =
RаFх/u = 3400·2,36/15 = 535 кгс/см. Рис. 26. К примеру расчета 20 По формуле (75)
вычисляем длину w, на которую надо завести
обрываемый стержень за точку теоретического обрыва: w = Q/(2qх) + 5d = 53200/(2·535) + 5·3,2 =
65,7 см > 20d = 20·3,2 = 64 см. Следовательно, из условия (75)
расстояние от опоры до места обрыва стержня может быть принято равным x + w= 39 + 65,7 = 104,7 см. Определяем необходимое
расстояние lан от места обрыва стержня до
вертикального сечения, в котором он используется полностью, по табл. 41 и п. 5.48: lан = 29d =
29·3,2 = 93 см < 104,7 см, следовательно, обрываем стержень на расстоянии 104,7
см от опоры. Пример
20. Дано:
примыкание сборной железобетонной второстепенной балки перекрытия к ригелю
осуществляется при помощи подрезки как показано на рис. 26; рабочая высота в
сечении консоли h01 = 37 см; в сечении балки h0 = 67 см; бетон марки М 300 (Rпр = 115 кгс/см2 и Rр = 8,5 кгс/см2 с
учетом mб1 = 0,85); хомуты и отогнутые
стержни из арматуры класса А-III (Rа = 3400 кгс/см2,
Rа.х = 2700 кгс/см2),
диаметрами соответственно 12 и 16 мм (Fх = Fх1 = 4,52 см2 Fо = 8,04 см2); шаг
хомутов u = 10 см, продольная рабочая
арматура класса А-III (Rа = 3400 кгс/см2),
площадью Fа = 6,16 см2 (4Æ14); поперечная сила на опоре Q =
64 тс. Требуется проверить прочность
наклонных сечений подрезки на действие поперечной силы и изгибающего момента. Расчет. Проверим прочность подрезки
по поперечной силе, принимая h0 = h01 = 37 см. Проверяем требование п. 3.30: 0,35Rпрbh0 = 0,35·115·73·37 = 108,7 тс
> Q = 64 тс. Так как 0,6Rрbh01 = 0,6·8,5·73·37 = 13,8 тс
< Q = 64 тс, согласно п. 3.31,
расчет по поперечной силе необходим. Определяем предельную
поперечную силу Qх.б, которую воспримут в
невыгоднейшем наклонном сечении совместно хомуты и бетон, по формуле (53). Для
этого по формуле (54) найдем усилие в хомутах на единицу длины
элемента: qх = Rа.хFх/u = 2700·4,52/10 = 1220 кгс/см;
Поскольку Qх.б = 91 тс > Q = 64 тс, даже без учета
отгибов прочность по поперечной силе обеспечена. Проверяем прочность
наклонного сечения, проходящего через входящий угол подрезки, на действие
изгибающего момента. Предварительно проверим
достаточность специальных хомутов и отгибов, установленных у конца подрезки, из
условия (77): Fх1 = 4,52 см2 (4Æ12); Fо = 8,04 см2 (4Æ16); α = 45°; RаFх1 + RаFоsinα = 3400·4,52 +
3400·8,04·0,707 = 34,7 тс > Q(1 - h01/h0) = 64(1 - 37/67) = 28,7 тс. Так как условие (77)
выполняется, прочность наклонного сечения проверяется из условия (78). Для этого вычисляем qхw qхw =
RаFх/u = 3400·4,52/10 = 1540 кгс/см. Изгибающий момент в сечении у
конца подрезки равен M = Qa0 = 64·0,13 = 8,3 тс·м; поскольку продольная растянутая арматура короткой
консоли заанкерена на опоре, учитываем эту арматуру с полным расчетным сопротивлением:
= 13,2 тс·м < 0,9h01(RаFа +
RаFоcosα) = 0,9·37(3400·6,16 +
3400·8,04·0,707) = 13,2 тс·м, т.е. прочность наклонного сечения по изгибающему
моменту обеспечена. Определим необходимую длину
заведения продольной растянутой арматуры за конец подрезки по формуле (76):
= 65 см > lан = 29d = 29·1,4 = 40,6 см (см. п. 5.48). Определяем длину l1, на которой устанавливаются
хомуты согласно п. 3.51: l1 = Q/qх + u = 64000/1220 + 10 = 62,4 см < w 0 = 65 см. Принимаем длину l1 = w0 = 65 см. Внецентренно-сжатые
элементы
Общие положения
3.53(1.22). При расчете по прочности железобетонных элементов на воздействие
продольной сжимающей силы N должен
приниматься во внимание случайный эксцентрицитет e0сл обусловленный не учтенными
в расчете факторами, в том числе неоднородностью свойств бетона по сечению
элемента. Эксцентрицитет e0сл в любом случае принимается
не менее следующих значений: 1/600 всей длины
элемента или длины его части (между точками закрепления элемента), учитываемой
в расчете; 1/30 высоты
сечения элемента; - 1 см. Для элементов статически
неопределимых конструкций (в том числе для колонн каркасных зданий) величина
эксцентрицитета продольной силы относительно центра тяжести приведенного
сечения e0 принимается равной
эксцентрицитету, полученному из статического расчета конструкции, но не менее e0сл. В элементах статически определимых
конструкций (например, фахверковые стойки, стойки ЛЭП) эксцентрицитет e0 находится как сумма
эксцентрицитетов - определяемого из статического расчета конструкции и
случайного. 3.54. Расчет внецентренно-сжатых элементов должен производиться с учетом
влияния прогиба элемента как в плоскости эксцентрицитета продольной силы (в
плоскости изгиба), так и в нормальной к ней плоскости. В последнем случае
принимается, что продольная сила приложена с эксцентрицитетом e0, равным
случайному эксцентрицитету e0сл (см. п. 3.51). Влияние прогиба элемента
учитывается согласно указаниям пп. 3.57 - 3.59. Расчет из плоскости изгиба
можно не производить, если гибкость элемента l0/r
(для прямоугольных сечений l0/h) в плоскости изгиба превышает гибкость в плоскости, нормальной
плоскости изгиба. При наличии расчетных
эксцентрицитетов в двух направлениях производится расчет на косое внецентренное
сжатие (см. пп. 3.75 - 3.77). 3.55. Для наиболее часто
встречающихся видов сжатых элементов (прямоугольного и двутаврового сечения с
симметрично расположенной арматурой, круглого и кольцевого сечения с арматурой,
равномерно распределенной по окружности) расчет по прочности нормальных сечений
производится согласно пп. 3.63 - 3.77. Для других видов сечений и
при произвольном расположении продольной арматуры расчет нормальных сечений
производится по формулам общего случая расчета согласно п. 3.78.
Если выполняется условие F'а
> 0,02F,
в расчетных
формулах пп. 3.63
- 3.78
следует учитывать уменьшение действительной площади бетона сжатой зоны на
величину F'а. 3.56. Проверка прочности
наклонных сечений внецентренно-сжатых элементов производится аналогично расчету
изгибаемых элементов в соответствии с указаниями пп. 3.29 - 3.52, за исключением условия (50) п. 3.33. Учет
влияния прогиба элемента
3.57. Влияние прогиба на величину эксцентрицитета продольного усилия следует
учитывать, как правило, путем расчета конструкций по деформированной схеме,
принимая во внимание неупругие деформации материалов и наличие трещин. Допускается производить
расчет конструкций по недеформированной схеме, учитывая влияние прогиба
элемента путем умножения эксцентрицитета e0 на коэффициент η, определяемый по формуле где Nкр - условная критическая сила,
определяемая по формулам: для элементов любой формы
сечения где I и Iа - моменты инерции
соответственно бетонного сечения и сечения всей арматуры относительно центра
тяжести бетонного сечения; для элементов прямоугольного
сечения kдл - коэффициент, учитывающий
влияние длительного действия нагрузки на прогиб элемента в предельном
состоянии, равный kдл = 1 + M1дл/M1; (82) M1 и M1дл - моменты внешних сил относительно оси, проходящей через центр
тяжести крайнего ряда арматуры, расположенного у растянутой (менее сжатой)
грани параллельно этой грани, соответственно от действия полной нагрузки и от
действия постоянной и длительной нагрузок: для элементов, рассчитываемых
согласно пп. 3.63,
3.64,
3.67
- 3.70,
допускается M1 и M1дл определять относительно оси,
проходящей через центр тяжести всей арматуры A; t - коэффициент, принимаемый
равным e0/h, но не менее величины tмин = 0,5 - 0,01l0/h -
0,001Rпр (83) (здесь Rпр, кгс/см2,
допускается принимать при mб1 = 1; значение h для круглых и кольцевых
сечений заменяется на D); l0 - принимается по указаниям
п. 3.59;
При расчете элементов
прямоугольного сечения с арматурой, симметрично расположенной по периметру
сечения (п. 3.65),
в значении (Fа + F'а) не учитывается 2/3
арматуры, расположенной у граней, параллельных плоскости изгиба (2Fа.п), а значение (h0 - a')/h в формуле (81)
принимается равным 1 - 2δ1. Эксцентрицитет e0, используемый в настоящем
пункте, допускается определять относительно центра тяжести бетонного сечения. При гибкости элемента l0/r < 14 (для прямоугольных сечений при l0/h
< 4) допускается принимать η = 1. При гибкости 14 < l0/r < 35 (4 < l0/h < 10) и при μ = (Fа + F'а)/F ≤ 0,025 допускается принимать: для прямоугольных сечений
для других форм сечения
При N ≥ Nкр следует увеличивать размеры
сечения. При расчетных
эксцентрицитетах в двух направлениях коэффициент η определяется отдельно
для каждого направления и умножается на соответствующий эксцентрицитет. 3.58. При расчете железобетонных элементов, имеющих несмещаемые опоры
(например, сжатые элементы раскосных ферм), а также если расчетные моменты в
сжатом элементе вызваны вынужденными деформациями от температурных воздействий,
смещений связевых диафрагм, удлинений затяжек арок и т.п. (например, колонны
связевых каркасов) значения коэффициента η принимаются: а) для сечений в средней
трети длины элемента - по формуле (79); б) для сечений в пределах
крайних третей длины элемента - путем линейной интерполяции, принимая в опорных
сечениях коэффициенты η равными единице. При расчете колонн
многоэтажных симметричных рам с жесткими узлами и при равном числе пролетов на
каждом этаже допускается окончательные моменты для сечений в пределах крайних
третей длины колонны принимать равными: M =
Mвηв + Mгηг, где Mв - момент от вертикальных
нагрузок на перекрытиях и покрытии и от указанных выше вынужденных деформаций; Mг -
момент от прочих нагрузок; ηв - коэффициент η, определяемый согласно подпункту
«б»; ηг - коэффициент η, определяемый по формуле (79); при определении коэффициентов
ηв и ηг учитываются все нагрузки. Здесь M, Mв и Mг - моменты внешних сил
относительно центра тяжести бетонного сечения. 3.59(3.25). Расчетные длины l0 внецентренно-сжатых железобетонных элементов рекомендуется определять
как для элементов рамной конструкции с учётом ее деформированного состояний при
наиболее невыгодном для данного элемента расположении нагрузки, принимая во
внимание неупругие деформации материалов и наличие трещин. Для элементов наиболее часто
встречающихся конструкций допускается принимать расчетные длины l0 равными: а) для колонн многоэтажных
зданий при числе пролетов не менее двух и соединениях ригелей и колонн,
рассчитываемых как жесткие, при конструкциях перекрытий: сборных - H; монолитных 0,7H, где H - высота этажа (расстояние между центрами узлов); б) для колонн одноэтажных
зданий с шарнирным стиранием несущих конструкций покрытий, жестких в своей
плоскости (способных передавать горизонтальные усилия), а также для эстакад -
по табл. 19; в) для элементов ферм и арок
- по табл. 20. Таблица 20(33)
Таблица 19(32)
Учет влияния косвенного армирования
3.60(3.22). Расчет элементов оплошного сечения с косвенным армированием в виде
сварных сеток, спиральной или кольцевой арматуры (рис. 27) следует производить
согласно указаниям пп. 3.63 - 3.70, 3.73 - 3.78 по сечению, ограниченному осями крайних стержней поперечной арматуры
(ядро сечения), подставляя в расчетные формулы вместо Rпр приведенную призменную прочность R*пр и вычисляя характеристику сжатой зоны бетона ξ0, с
учетом влияния косвенного армирования по формуле (90). Влияние прогиба элемента с
косвенным армированием на эксцентрицитет продольной силы учитывается согласно
указаниям п. 3.61. Рис. 27. Сжатые элементы с
косвенным армированием в виде а - сварных сеток; б - спиральной арматуры Значения R*пр
определяются по формулам: а) при армировании сварными
поперечными сетками R*пр = Rпр + kμскRса, (85) где k - коэффициент эффективности
косвенного армирования, принимаемый равным μск - коэффициент косвенного
армирования сетками, равный n1, fс1, l1 - соответственно число стержней, площадь поперечного сечения и
длина стержня сетки в одном направлении (считая в осях крайних стержней); n2, fс2, l2 - то же, в другом направлении; s -
расстояние между сетками; Fя - площадь ядра бетонного сечения, заключенного внутри
контура сеток (считая в осях крайних стержней); Rса - расчетное сопротивление арматуры сеток; б) при армировании спиральной
и кольцевой арматурой R*пр = Rпр + 2μспкRспа(1 - 7,5e0/dя), (89) где μспк -
коэффициент косвенного армирования спиралью (кольцами), равный
fсп - площадь поперечного сечения спиральной арматуры; dя - диаметр ядра бетонного сечения; s - шаг навивки спирали или расстояние между кольцами; Rспа - расчетное
сопротивление арматуры спирали (колец). Эксцентрицитет e0 в формуле (89)
можно определять без учета прогиба элемента. Значение ξ0 при косвенном армировании
определяется по формуле ξ0 = 0,85 - 0,0008Rпр + но принимается не более 0,9. В формуле (90): Rпр - в кгс/см2,
Косвенное армирование
учитывается в расчете при гибкости l0/rя ≤ 35 (для
прямоугольных сечений при l0/hя ≤ 10, где rя и hя - радиус инерции и высота
ядра сечения), а также при условии, что несущая способность элемента,
определенная согласно указаниям настоящего пункта (вводя в расчет Fя и R*пр), превышает его несущую
способность, определенную по полному сечению F и
величине расчетного сопротивления бетона Rпр (без учета косвенной
арматуры). Кроме того, косвенное
армирование должно удовлетворять конструктивным требованиям пп. 5.82 - 5.84. 3.61(3.22). При расчете элементов с косвенным армированием по недеформированной
схеме влияние прогиба элемента на эксцентрицитет продольной силы учитывается
согласно п. 3.57 - 3.59; при этом величина Nкр, полученная по формуле (80) или (81), умножается на коэффициент
kс = 0,25 + 0,05l0/hя,
а значение tмин вычисляется
по формуле tмин = 0,5 + 0,01l0/hя(1 - 0,1l0/hя) - 0,001Rпр, где hя - высота бетонного ядра сечения (для круглых сечений hя заменяется на dя).
Кроме того, при
вычислении Nкр размеры сечения принимаются
по ядру бетонного сечения. 3.62(3.23). При расчете внецентренно-сжатых элементов с косвенным армированием
наряду с расчетом по прочности согласно п. 3.60 должно соблюдаться условие,
обеспечивающее трещиностойкость защитного слоя: где Fп и Iп - соответственно площадь и момент инерции полного приведенного
сечения элемента; y - расстояние от центра тяжести
приведенного сечения до наиболее сжатого волокна. При определении Fп, Iп и y в
формуле (91)
коэффициент приведения арматуры к бетону принимается равным n = 0,65Rа/Rпр или по табл. 21. Таблица 21
Эксцентрицитет продольной
силы e0 в
формуле (91)
определяется с учетом прогиба элемента согласно п. 3.57 - 3.59 и 3.61. Расчет
элементов симметричного сечения при расположении продольной силы в плоскости
симметрии
Прямоугольные сечения с
симметричной арматурой
3.63(3.20). Проверка прочности прямоугольных сечений с симметричной арматурой,
сосредоточенной у наиболее сжатой и у растянутой (наименее сжатой) граней
элемента, производится следующим образом в зависимости от высоты сжатой зоны а) при x
≤ ξRh0 (рис. 28) из
условия Ne
≤ Rпрbx(h0 - 0,5x) + Rа.сF'а(h0 - a'); (93) б) при x
> ξRh0 также из условия (93),
принимая высоту сжатой зоны, равной x = ξh0, где значение ξ определяется по формулам: для элементов из бетона марки
М 400 и ниже для элементов из бетона
марки выше М 400 Рис. 28. Схема усилий в поперечном
прямоугольном сечении внецентренно-сжатого элемента 1 - сжатая зона
ξR, ξ0 и s - см. табл. 17 п. 3.15. Значение e вычисляется по формуле e = e0 + (h0
- a')/2. (96) При этом эксцентрицитет
продольной силы e0 относительно центра тяжести
сечения определяется с учетом прогиба элемента согласно пп. 3.57 - 3.59. Примечания: 1. Если высота сжатой зоны, определенная с учетом
половины сжатой арматуры, 2. Формулой (95) можно пользоваться также
при расчете элементов из бетона марки М 400 и ниже. 3.64.
Определение требуемого количества симметричной
арматуры производится следующим образом в зависимости от относительной величины
продольной силы а) при б) при где относительная высота сжатой зоны ξ
определяется по формуле (94) или (95) п. 3.63; при этом в формуле (94)
значение α допускается определять по формуле а в формуле (95) - тоже по формуле (99) с
заменой
Значение e вычисляется по формуле (96) п. 3.63.
Рис. 29. Графики несущей
способности внецентренно-сжатых элементов прямоугольного сечения с симметричной
арматурой сплошная линия при M1дл/M1 = 1 (см. п. 3.57); пунктирная при M1дл/M1 = 0,5;
Примечания:
1. Графиками допускается пользоваться при марках бетона от М 200 до М 600 и при
a = a' от 0,05h0 до 0,15h0. 2. При M1дл/M1 < 0,5 значения α определяются линейной экстраполяцией. Если значение a' не превышает 0,15h0, необходимое количество
арматуры можно определять с помощью графика рис. 29,а, используя формулу
где α определяется
по графику в зависимости от значений:
при этом значение момента M относительно
центра тяжести сечения определяется с учетом прогиба элемента согласно пп. 3.57 - 3.59. При статическом расчете по
недеформированной схеме и при использовании коэффициента η
> 1 подбор арматуры по вышеприведенным формулам и графику производится в
общем случае путем последовательных приближений. Для элементов из бетона марок
от М 200 до М 600 при λ = l0/h ≤ 25 и при a' не более 0,15h0 подбор арматуры можно
производить без последовательных приближений с помощью графиков на рис. 29, при
этом используются значения M без учета коэффициента η. Рис. 30. Схема, принимаемая
при расчете внецентренно-сжатого
элемента прямоугольного сечения с арматурой, расположенной по высоте сечения 3.65.
При наличии арматуры, расположенной по высоте
сечения, расчет внецентренно-сжатых элементов допускается производить по
формулам (102) и (103), рассматривая всю арматуру как равномерно распределенную по линиям
центров тяжести стержней (рис. 30). При этом площадь сечения
арматуры Fа.и, расположенной у одной из
граней, параллельных плоскости изгиба, принимается равной Fа.и = fп.и(pи + 1), (100) где fп.и - площадь одного промежуточного стержня этой арматуры; при разных
диаметрах промежуточных стержней принимается средняя площадь сечения
промежуточного стержня; pи -
число промежуточных стержней этой арматуры. Площадь сечения арматуры Fа.п, расположенной у одной из
граней, перпендикулярных к плоскости изгиба, равна Fа.п = Σfа/2 - Fа.и, (101) где Σfа -
площадь всей арматуры в сечении элемента. Проверка прочности сечения
производится в зависимости от относительной высоты сжатой зоны: а) при ξ ≤ ξR прочность сечения проверяется
из условия Ne0 ≤ Rпрbh2[0,5ξ(1 - ξ) + αи(ξ1 - δ1)(1 - ξ1 - δ1) - 0,05αиξ12 + αп(1 - 2δ1)], (102) где ξ1 = ξ/ξ0;
б) при ξ > ξR прочность сечения
проверяется из условия Ne0 ≤ Rпрbh2mгр(nц - n1)/(nц - nгр), (103) где mгр и nгр - относительные величины соответственно изгибающего момента и
продольной силы при высоте сжатой зоны ξRh, равные mгр = 0,5ξR(1 - ξR) + αи(ξ1R - δ1)(1 - ξ1R - δ1) - 0,05αиξ21R + αп(1 - 2δ1); nгр = ξR + αи(2ξ1R - 1); ξ1R = ξR/ξ0; ξR и ξ0 - см. п. 3.15
табл. 17. Эксцентрицитет продольной
силы e0 определяется
с учетом прогиба элемента согласно п. 3.57 - 3.59. Примечание.
При расположении арматуры в пределах крайних четвертей высоты h - 2a1 (см.
рис. 30)
расчет надо производить согласно указаниям пп. 3.63 и 3.64, рассматривая арматуру A и A' сосредоточенной по
линиям их центров тяжести. 3.66(прил.
2). Расчет сжатого элемента с
учетом его прогиба на действие продольной силы, приложенной с эксцентрицитетом,
принятым согласно п. 3.53, равным случайному эксцентрицитету e0сл, при l ≤ 20h допускается производить из
условия N ≤ mφ(RпрF + Rа.сΣfа), (104) где m -
коэффициент, принимаемый равным: при h
> 20 см - 1, а при h
≤ 20 см - 0,9; φ - коэффициент, определяемый по формуле φ = φб + 2(φж - φб)α, (105) но принимаемый не более φж; здесь φб и φж -
коэффициенты, принимаемые по табл. 22 и 23;
Σfа - см. п. 3.65. При α > 0,5 можно, не
пользуясь формулой (105), принимать φ = φж. Таблица 22 (1 прил. 2) Значения коэффициента φб
Таблица 23 (2 прил. 2) Значения коэффициента φж
Nдл - продольная сила от действия постоянных и длительных нагрузок; N - продольная сила от действия постоянных,
длительных и кратковременных нагрузок; 1-1 -
рассматриваемая плоскость; 2 - промежуточные стержни. Примечание. При промежуточных значениях l0/h и Nдл/N коэффициенты
φб и φж определяются по интерполяции. Прямоугольные сечения с несимметричной арматурой3.67. Проверка прочности прямоугольных сечений с несимметричной арматурой,
сосредоточенной у наиболее сжатой и у растянутой (наименее сжатой) граней
элемента, производится согласно п. 3.63, при этом формулы (92), (94) и (95) приобретают вид:
где
3.68. Площади сечения сжатой и
растянутой арматуры, соответствующие минимуму их суммы, определяются по
формулам: для элементов из бетона марок
М 400 и ниже: для элементов из бетона марок
выше М 400: где AR и ξR
- определяются по табл. 17 п. 3.15 и принимаются не более
соответственно 0,4 и 0,55. При отрицательном значении Fа, вычисленном по формуле (107)
или (109),
площадь арматуры A принимается минимальной из
конструктивных требований, но не менее величины При отрицательном значении Fа.мин, вычисленном по формуле (110),
площадь сечения арматуры A' определяется по формуле
а при положительном значении Fа.мин, - по формуле
Если принятая площадь
сечения сжатой арматуры F'а.ф значительно превышает ее значение, вычисленное по формулам (106) и
(108)
(например, при отрицательном значении F'а),
то площадь
сечения растянутой арматуры может быть уменьшена исходя из формулы
где ξ определяется по табл. 18 п. 3.19 в
зависимости от значения
Двутавровые сечения с
симметричной арматурой
3.69. Проверка прочности двутавровых сечений с симметричной арматурой,
сосредоточенной в полках (рис. 31), производится следующим
образом. Если соблюдается условие N ≤ Rпрb'пhп' (114) (т.е. граница сжатой зоны проходит в полке), то
расчет производится как для прямоугольного сечения шириной b'п в соответствии с указаниями
п. 3.63. Если условие (114) не
соблюдается (т.е. граница сжатой зоны проходит в ребре), расчет производится в
зависимости от высоты сжатой зоны а) при x ≤ ξRh0 прочность сечения
проверяется из условия Nе ≤ Rпрbх(h0 - x/2) + RпрFсв(h0 - hп'/2) + Rа.сF'а(h0 - a'); (115) б) при x > ξRh0 прочность сечения проверяется также из условия (115),
определяя высоту сжатой зоны по формуле Рис. 31. Схема усилий в
поперечном двутавровом сечении внецентренно-сжатого элемента где
s, ξR и ξ0 - см. табл. 17 п. 3.15; Fсв - площадь сжатых свесов
полки: Fсв = (b'п - b)h'п. Если значение x, определенное по формуле (116),
превышает h - h'п (т.е. граница сжатой зоны
проходит по менее сжатой полке), можно учесть повышение несущей способности
сечения за счет включения в работу менее сжатой полки. Расчет при этом, если b'п
= bп, производится по формулам (115) и (116) с
заменой b на bп; h'п на (h + h'п -
hп) и Fсв = -(bп - b)(h - hп -
h'п). Примечание.
При переменной высоте свесов полок значения hп и h'п принимаются равными средней высоте свесов. 3.70. Определение требуемого количества симметричной арматуры двутавровых
сечений производится следующим образом. При соблюдении условия (114)
подбор арматуры производится как для прямоугольного сечения шириной b'п
согласно указаниям п. 3.64. Если условие (114) не
соблюдается, подбор арматуры производится в зависимости от относительной высоты
сжатой зоны ξ = а) при ξ ≤ ξR
б) при ξ > ξR где относительная высота сжатой зоны ξ1 = x/h0 определяется из формулы (116),
при этом для бетона марки М 400 и ниже в формуле (120)
можно принять ξ2 = ξ. В формулах (117) -
(120):
Кольцевые сечения (рис. 32)
3.71(3.21). Проверка прочности кольцевых сечений при соотношении внутреннего и
наружного радиусов r1/r2 ≥ 0,5 с арматурой,
равномерно распределенной по окружности (при числе продольных стержней не менее
6), производится следующим образом в зависимости от относительной площади
сжатой зоны бетона Рис. 32. Схема, принимаемая
при расчете кольцевого сечения внецентренно-сжатого элемента 1 - сжатая зона а) при 0,15 ≤ αк ≤ 0,6 из условия Ne0 ≤ (RпрFrср + RаFа.кrа) б) при αк < 0,15 из условия Ne0 ≤ (RпрFrср + RаFа.кrа) где в) при αк > 0,6 из условия Ne0 ≤ (RпрFrср + RаFа.кrа) где Fа.к - площадь сечения всей продольной арматуры;
rа - радиус окружности, проходящей через центры тяжести стержней
продольной арматуры. Эксцентрицитет продольной
силы e0 определяется с учетом прогиба
элемента согласно п. 3.57 - 3.59. 3.72. Проверку прочности, а также определение необходимого количества
продольной арматуры для кольцевых сечений, указанных в п. 3.71, при rа ≈ rср допускается производить при
помощи графиков на рис. 33, используя формулы: Ne0 ≤ A0кRпрrсрF; (127)
где значения A0к и α определяются по
графику в зависимости от значений соответственно Рис. 33. Графики несущей
способности внецентренно-сжатых элементов кольцевого сечения
Круглые сечения (рис. 34)
3.73. Проверка прочности круглых сечений с арматурой, равномерно
распределенной по окружности (при числе продольных стержней не менее 6), при
марках бетона не более М 400 производится из условия Ne0 ≤ где r - радиус
поперечного сечения; αк -
относительная площадь сжатой зоны бетона, определяемая следующим образом. Рис. 34. Схема, принимаемая
при расчете круглого сечения внецентренно-сжатого элемента 1 - сжатая зона При выполнении условия N ≤ 0,77RпрF + 0,645RаFа.к (130) из решения уравнения
При невыполнении условия (130) -
из решения уравнения
k -
коэффициент, учитывающий работу растянутой арматуры и принимаемый равным: при выполнении условия (130) - k =
1,6(1 - 1,55αк)αк, но не более единицы, при
невыполнении условия (130) - k
= 0; Fа.к - площадь сечения всей продольной арматуры; rа - радиус окружности, проходящей через центры тяжести стержней
продольной арматуры. Эксцентрицитет продольной
силы e0 определяется с учетом
прогиба элемента согласно пп. 3.57 - 3.59. 3.74. Проверку прочности, а также
определение необходимого количества продольной арматуры для круглых сечений,
указанных в п. 3.73,
допускается производить при помощи графиков на рис. 35, используя формулы: Ne0 ≤ A0крRпрFr; (133)
где A0кр и α определяются по
графику в зависимости от значений соответственно: Рис. 35. Графики несущей
способности внецентренно-сжатых элементов круглого сечения
Расчет элементов, работающих на косое внецентренное сжатие
3.75. Расчет нормальных сечений элементов, работающих на косое внецентренное
сжатие, производится в общем случае согласно указаниям, приведенным в п. 3.78, определяя положение прямой,
ограничивающей сжатую зону, при помощи последовательных приближений. 3.76. Расчет элементов прямоугольного сечения с симметричной арматурой на
косое внецентренное сжатие допускается производить с помощью графиков,
представленных на рис. 36. Прочность сечения считается
обеспеченной, если точки с координатами Mх/Mх0 Mу/Mу0 на графике, отвечающем
параметру α, находятся внутри области, ограниченной кривой, отвечающей
параметру n1, и осями координат. Значения Mх и Mу представляют собой изгибающие
моменты от внешней нагрузки относительно центра тяжести сечения, действующие
соответственно в плоскостях симметрии x и y. Влияние прогиба элемента учитывается путем умножения моментов Mх и Mу на коэффициенты ηх и ηу, определяемые соответственно
для плоскостей x и y, согласно указаниям п. 3.57,
при действующей продольной силе N. Значения Mх0 и Mу0 представляют собой предельные
изгибающие моменты, которые могут восприниматься сечением в плоскостях
симметрии x и y с учетом действующей продольной силы N, приложенной в центре
тяжести сечения. Величины предельных моментов Mх0 и Mу0 представляют собой правые
части условий (102) и (103) п. 3.65.
При этом дискретно расположенные стержни арматуры заменяются распределенным
армированием Fах
= fпх(pх + 1) + (2f0 - fпх
- fпу)B/(1 + B); (135) Fау = Σfа - Fа.х, (136) где Fах, Fау - площади арматуры, расположенной у граней, нормальных
осям симметрии x и y (рис. 37); fпх, fпу - площадь каждого из промежуточных стержней,
расположенных у граней, нормальных осям симметрии x и y; pх -
число промежуточных стержней fпх, расположенных по одной
стороне сечения; f0 -
площадь углового стержня;
hх и hу - высота сечения соответственно при внецентренном
сжатии в плоскостях x и y; Σfа - площадь сечения всей продольной арматуры.
Рис. 36. Графики несущей
способности элементов прямоугольного сечения с симметричной арматурой,
работающих на косое внецентренное сжатие
Рис. 37. Обозначения,
принятые при расчете на косое внецентренное сжатие прямоугольных сечений с
симметрично расположенной арматурой Параметры α и n1 определяются из формул
3.77. Расчет элементов симметричного двутаврового сечения при bп/b = 3 ÷ 5 и hп/h = 0,15 ÷ 0,25 с
симметричной арматурой, расположенной в полках сечения, на косое внецентренное
сжатие допускается производить с помощью графиков несущей способности,
представленных на рис. 38. Расчет производится
аналогично расчету, приведенному в п. 3.76 для элементов
прямоугольного сечения. Предельные моменты Mх0, которые могут восприниматься
сечением в плоскости оси симметрии x, проходящей в ребре, представляют собой правую часть условия (115) п.
3.69,
уменьшенную на N(h0 - a')/2,
а предельные моменты Mу0 во взаимно перпендикулярной
плоскости симметрии y допускается
определять как для прямоугольного сечения, составленного из двух полок,
согласно п. 3.65. Общий случай расчета нормальных сечений
внецентренно-сжатого элемента
(при
любых сечениях, внешних усилиях и любом
армировании) 3.78(3.28). Расчет сечений внецентренно-сжатого элемента в общем случае (рис. 39) должен производиться из
условия N где Sб - статический момент площади сжатой зоны бетона относительно
указанной оси; Sаi - статический момент площади сечения i-го стержня продольной
арматуры относительно указанной оси; σаi - напряжение в i-м стержне продольной
арматуры.
Рис. 38. Графики несущей
способности элементов симметричного двутаврового сечения, работающих на косое
внецентренное сжатие
Высота сжатой зоны x и напряжения σаi, кгс/см2
определяются из совместного решения уравнений: RпрFб - Σσаifаi - N = 0; (138) fаi - площадь сечения i-го стержня продольной арматуры; ξi - относительная
высота сжатой зоны бетона, равная ξi
= x/h0i, где h0i - расстояние от оси, проходящей через центр тяжести сечения
рассматриваемого i-го стержня арматуры и параллельной прямой, ограничивающей сжатую
зону, до наиболее удаленной точки сжатой зоны сечения (рис. 39); ξ0 -
характеристика сжатой зоны бетона, определяемая по формуле (19) п. 3.15 или
(90)
п. 3.60; σε - см. п. 3.15. Напряжения σаi
вводятся в расчетные формулы со своими знаками, полученными при расчете по
формуле (139),
при этом напряжения со знаком плюс означают растягивающие напряжения и принимаются
не более Rаi,
а напряжения со знаком минус означают сжимающие напряжения и принимаются по
абсолютной величине не более Rа.с. Рис. 39. Схема усилий и эпюра
напряжений в сечении, нормальном к продольной оси железобетонного элемента, в
общем случае расчета по прочности 1-1 - плоскость,
параллельная плоскости действия изгибающего момента, или плоскость, проходящая
через точки приложения продольной силы и равнодействующих внутренних сжимающих
и растягивающих усилий; А - точка приложения равнодействующих
усилий в сжатой арматуре и в бетоне сжатой зоны; Б - точка приложения равнодействующей
усилий в растянутой арматуре Для определения положения
границы сжатой зоны при косом внецентренном сжатии кроме использования формул (138) и
(139)
требуется соблюдение дополнительного условия, чтобы точки приложения внешней
продольной силы, равнодействующей сжимающих усилий в бетоне и арматуре и
равнодействующей усилий в растянутой арматуре лежали на одной прямой (рис. 39). Если в сечении можно выявить
характерную ось (например, оси симметрии или ось ребра Г-образного сечения), то
при косом внецентренном сжатии вместо соблюдения вышеуказанного дополнительного
условия рекомендуется вести расчет из двух условий: из условия (137),
определяя значения При этом положение прямой,
ограничивающей сжатую зону, подбирают последовательными приближениями из
уравнений (138)
и (139),
принимая угол наклона этой прямой γ
постоянным и равным углу наклона нейтральной оси, определенному как для
упругого материала. Прочность сечения будет
обеспечена лишь при соблюдении обоих условий. Если оба условия не соблюдаются,
прочность не обеспечена и следует увеличить армирование, размеры сечения или
повысить марку бетона. Если одно условие соблюдается, а другое не соблюдается,
следует снова определить очертание сжатой зоны при другом угле γ и провести аналогичный расчет. Примеры
расчета
Внецентренно-сжатые
элементы Прямоугольные
сечения с симметричной арматурой Пример
21. Дано:
колонна рамного каркаса с размерами сечения b = 40 см; h = 50 см; a = a' = 4
см; бетон марки М 300; арматура класса А-III (Rа = Rа.с
= 3400 кгс/см2; Eа = 2·106 кгс/см2)
площадью сечения Fа = F'а =
12,32 см2
(2Æ28); продольные силы и
изгибающие моменты: от постоянных и длительных нагрузок Nдл = 65 тс, Mдл = 14 тс·м; от ветровой нагрузки Nк = 5 тс, Mк =
7,3 тс·м; расчетная длина колонны l0 = 6 м. Требуется проверить прочность
сечения колонны. Расчет. h0 = 50 - 4 = 46 см. Поскольку имеют место усилия от
нагрузки малой суммарной длительности действия (ветровой), согласно п. 3.1,
установим значения вводимого в расчет расчетного сопротивления бетона Rпр. Усилия от всех нагрузок
равны: N = 65 + 5 = 70 тс; M =
14 + 7,3 = 21,3 тс·м. Определим моменты внешних сил
относительно растянутой арматуры от постоянных, длительных и кратковременных
нагрузок, подсчитанных соответственно с учетом и без учета нагрузки малой
суммарной длительности (ветровой): MII = M1 = M + N(h0 - a')/2 = 21,3 + 70(0,46 - 0,04)/2 = 36 тс·м; MI = M1дл = Mдл + Nдл(h0 - a')/2 = 14 + 65(0,46 - 0,04)/2 = 27,65 тс·м. Так как 0,77MII = 0,77·36 = 27,7 тс·м > MI = 27,65 тс·м, то производим расчет только по случаю
«б» (см. п. 3.1),
т.е. на действие всех нагрузок, принимая Rпр = 145 кгс/см2 (при mб1 = 1,1). Так как l0/h = 600/50 = 12 > 10, то расчет ведем с учетом прогиба колонны,
согласно п. 3.57,
вычисляя Nкр по формуле (81). Для этого определим: kдл = 1 + M1дл/M1 = 1 + 27,65/36 = 1,77;
e0 = M/N = 2130/70 = 30,4 см > e0сл =
h/30 (см. п. 3.53), следовательно, случайный эксцентрицитет не учитываем. Так как e0/h = 30,4/50 = 0,608 > tмин = 0,5 - 0,01λ -
0,001Rпр = 0,5 - 0,01·12 -
0,001·145 = 0,235, то принимаем t = e0/h = 0,608.
Коэффициент η
определяем по формуле (79):
Значение e равно e = e0η +
(h0 - a')/2
= 30,4·1,12 + 0,5(46 - 4) = 55 см. Определяем высоту сжатой зоны
x по формуле (92): x =
N/(Rпрb) = 70000/(145·40) = 12,07
см; ξR = 0,572 (см. табл. 17). Так как x = 12,07 см < ξRh0 = 0,572·46 = 26,3 см, то
прочность сечения проверяем из условия (93). Rпрbx(h0 - 0,5x) + Rа.сF'а(h0 - a') = 145·40·12,07(46 -
0,5·12,07) + 3400·12,32(46 - 4) = 45,7 тс·м > Ne = 70·0,55 = 38,5 тс·м, т.е. прочность сечения обеспечена. Пример
22. Дано:
колонна связевого каркаса с размерами сечения b = 40 см; h = 50 см и длиной 6 м; a = a' = 4
см; бетон марки М 300 (Eб = 2,6·105 кгс/см2);
арматура класса А-III (Rа = Rа.с = 3400 кгс/см2, Eа = 2·106 кгс/см2)
площадью сечения Fа = F'а = 12,32 см2 (2Æ28); расчетные продольная сила и изгибающий момент в опорном сечении от
постоянных и длительных нагрузок N =
200 тс, M = 18 тс·м, прочие нагрузки
не учитываются. Требуется проверить прочность
опорного сечения. Расчет. h0 = 50 - 4 = 46 см. Поскольку нагрузки малой суммарной
длительности действия отсутствуют, согласно п. 3.1, принимаем Rпр = 115 кгс/см2
(т.е. при mб1 = 0,85). Согласно п. 3.58,
для опорного сечения колонны связевого каркаса принимаем η =
1. Определяем величину
случайного эксцентрицитета согласно п. 3.53: e0сл = h/30
= 50/30 = 1,7 см > l/600
= 600/600 = 1 см; e0 = M/N = 1800/200 = 9 см > e0сл =
1,7 см. Следовательно, случайный
эксцентрицитет не учитываем. Значение e равно e = e0 + (h0 - a')/2
= 9 + (46 - 4)/2 = 30 см. Определяем высоту сжатой зоны
x по формуле (92): x =
N/(Rпрb) = 200000/(115·40) = 43,5
см. Из табл. 17
находим ξR
= 0,625. Так как x =
43,5 см > ξRh0 =
0,625·46 = 28,8
см, то значение x вычисляем
согласно указаниям п. 3.63 «б»:
откуда x = ξh0·= 0,781·46 = 35,9 см. Проверяем прочность сечения
из условия (93): Rпрbx(h0 - 0,5x) + Rа.сF'а(h0 - a') = 115·40·35,9(46 -
0,5·35,9) + 3400·12,32(46 - 4) = 6390000 кгс·см = 63,9 тс·м > Ne = 200·0,3 = 60 тс·м, т.е. прочность сечения обеспечена. Пример 23. Дано: размеры сечения элемента b = 40 см; h = 50 см; a = a' = 4 см; бетон марки М 300 (Eб = 2,6·105 кгс/см2);
арматура симметричная класса А-III (Rа = Rа.с = 3400 кгс/см2, Eа = 2·10б кгс/см2); продольные силы и изгибающие
моменты: от длительных и постоянных нагрузок Nдл = 60 тс, Mдл = 17 тс·м; от ветровых
нагрузок Nк = 20 тс, Mк =
11 тс·м; расчетная длина l0 = 8 м. Требуется определить площадь
сечения арматуры. Расчет. h0 = 50 - 4 = 46 см. Поскольку имеет место усилие от
ветровой нагрузки, проверим условие (1) п. 3.1. Для этого вычислим: MI = M1дл =
Mдл + Nдл(h0 - a')/2 = 17 + 60(0,46 - 0,04)/2
= 29,6 тс·м; M = Mдл + Mк = 17 + 11 = 28 тс·м; N = Nдл + Nк = 60 + 20 = 80 тс; MII = M1 = M + N(h0 - a')/2 = 28 + 80(0,46 - 0,04)/2 = 44,8 тс·м; Так как 0,77MII = 0,77·44,8 = 34,5 тс·м > MI = 29,6 тс·м, то расчет производим только по случаю
«б», т.е. на действие всех нагрузок, принимая Rпр = 145 кгс/см2
(при mб1 =
1,1). Так как l0/h = 8/0,5 = 16 > 10, расчет ведем с учетом прогиба элемента, согласно
п. 3.57,
вычисляя Nкр по формуле (81). Для этого определим: kдл = 1 + M1дл/M1 = 1 + 29,6/44,8 = 1,66; e0 = M/N = 2800/80 = 35 см > e0сл =
h/30 (см. п. 3.53). Так как e0/h = 35/50 = 0,7 > tмин = 0,5 - 0,01l0/h - 0,001Rпр,
принимаем t = e0/h = 0,7. В первом приближении
принимаем μ = 0,01, n = Eа/Eб = 20·105/2,6·105 = 7,7. Тогда
= 325·104(0,0477 +
0,0543) = 332 тс. Коэффициент η
равен
Значение e с учетом прогиба элемента равно: e = e0η + (h0
- a')/2 = 35·1,32 + 0,5(46 - 4) =
67,1 см. Необходимое армирование
определяем согласно п. 3.64. Вычисляем значение:
δ = a'/h0 =
4/46 = 0,087. Из табл. 17
находим ξR
= 0,572. Так как
откуда μ = (Fа +
F'а)/(bh) =
2·15,67/(40·50) = 0,0157 > 0,01. Поскольку полученное
армирование существенно превышает армирование, принятое при определении Nкр (μ = 0,01), значение Fа = 15,67 см2
определено с «запасом» и его можно несколько уменьшить, уточнив значение μ. Принимаем μ =
(0,01 + 0,0157)/2 = 0,0128 и снова аналогично вычисляем значение Fа =
F'а:
e =
35·1,265 + 21 = 65,3 см;
Окончательно принимаем Fа =
F'а = 14,73 см2 (3Æ25). Пример
24. Дано:
колонна многоэтажного рамного симметричного каркаса с размерами сечения b = 40 см; h = 50 см; a = a' = 4
см; бетон марки М 300 (Eб = 2,6·105 кгс/см2);
арматура симметричная класса А-III (Rа = Rа.с = 3400 кгс/см2, Eа = 2·106 кгс/см2);
продольные силы и изгибающие моменты в опорном сечении колонны: от постоянных и
длительных нагрузок на перекрытиях Nдл = 220 тс, Mдл = 25,9 тс·м; от ветровых
нагрузок Nк = 0, Mк = 5,34 тс·м; кратковременные
нагрузки на перекрытиях отсутствуют; расчетная длина колонны l0 = 6 м. Требуется определить площадь
сечения арматуры. Расчет. h0 = h - a = 50 - 4 = 46 см. Поскольку
имеет место усилие от ветровой нагрузки, проверим условие (1) п. 3.1. Для
этого вычислим: MI = M1дл =
Mдл + Nдл(h0 - a')/2 = 25,9 + 220(0,46 -
0,04)/2 = 72,1 тс·м; M = Mдл + Mк = 25,9 + 5,34 = 32,24 тс·м; N = Nдл = 220 тс; MII = M1 = M + N(h0 - a')/2 = 32,24 + 220(0,46 - 0,04)/2 =
78,44 тс·м. Так как 0,77MII = 0,77·78,44 = 60,4 тс·м < MI = 72,1 тс·м, условие (1) не выполняется и расчет
производим дважды: по случаю «а» - на действие длительных и постоянных нагрузок
при Rпр = 115 кгс/см2
(т.е. при mб1 = 0,85) и по случаю «б» - на
действие всех нагрузок при Rпр = 145 кгс/см2
(т.е. при mб1 = 1,1). Расчет по случаю «а». Так как l0/h = 600/50 = 12 > 4, согласно п. 3.57, следует учитывать прогиб
колонны. Однако, согласно п. 3.58, для колонн многоэтажных симметричных рам со
всеми жесткими узлами коэффициент ηв, вводимый на момент Mв от нагрузок на перекрытиях,
принимается равным единице, а момент Mг =
Mк от ветровых нагрузок в данном
расчете не учитывается. Поэтому расчетный момент равен M = Mвηв = 25,9
тс·м. Расчетная продольная сила
равна N = Nдл = 220 тс, отсюда e0 = M/N = 2590/220 = 11,8 см > e0сл = h/30 = 50/30 = 1,67 см. Оставляем e0 = 11,8 см. По формуле (96)
определяем значение e = e0 + (h0
- a')/2 = 11,8 + (46 - 4)/2 = 32,8 см. Необходимое армирование
определяем согласно п. 3.64. Вычисляем значения:
δ = a'/h0 =
4/46 = 0,087. Из табл. 17
находим ξR = 0,625. Так как
Отсюда
Расчет по случаю «б». Согласно п. 3.57
определим коэффициент η, задаваясь армированием,
полученным из расчета по случаю «а», т.е. μ = 2Fа/(bh) = 2·17,8/(40·50) = 0,0178; kдл = 1 + M1дл/M1 = 1 + 72,1/78,44 = 1,92; e0 = M/N = 3224/220 = 14,65 см. Так как e0/h = 14,65/50 = 0,293 > tмин = 0,5 - 0,01l0/h - 0,001Rпр = 0,5 -
0,01·12 - 0,001·145 = 0,235, принимаем t = e0/h = 0,293.
По формуле (81)
определим Nкр:
Отсюда коэффициент η
равен
Согласно п. 3.58,
коэффициент η = ηг = 1,31 умножается на момент от ветровых
нагрузок Mк = Mг, а коэффициент ηв
= 1, поэтому момент с учетом прогиба колонны равен M = Mвηв + Mгηг = 25,9 +
5,34·1,31 = 32,9 тс·м. Необходимое армирование
определяем согласно п. 3.64 аналогично расчету по случаю «а», принимая Rпр = 145 кгс/см2: e = e0 + (h0
- a')/2 = 3290/220 + (46 - 4)/2 = 36 см;
Из табл. 17
находим ξR = 0,572. Так как
отсюда
Окончательно принимаем Fа = 18,47 см2 (3Æ28) > 17,80 см2. Пример
25. По
данным примера 23
надо определить требуемую площадь арматуры, используя график на рис. 29. Расчет. В соответствии с примером 23, имеем
N = 80 тс; M = 28 тс·м; λ = l0/h = 16; M1дл/M1 = 29,6/44,8 = 0,66. Определяем значения
По графику на рис. 29,в
при По графику рис. 29,г
при Значение α,
соответствующее λ = 16, находим линейной интерполяцией: α = 0,176 + (0,22 - 0,176)(16
- 15)/(20 - 15) = 0,185. Отсюда площадь сечения
арматуры равна
Принимаем Fа =
F'а = 14,73 см2 (3Æ25). Пример
26. Дано:
размеры сечения элемента b =
40 см; h = 60 см; бетон марки М 300 (Rпр = 145 кгс/см2
с учетом mб1 =
1,1; Eб = 2,6·105 кгс/см2); арматура
класса А-III (Rа = Rа.с = 6400 кгс/см2, Eа = 2·106 кгс/см2)
расположена в сечении, как показано на рис. 40; продольные силы и
изгибающие моменты: от всех нагрузок N = 50 тс, M =
50 тс·м; от постоянных и длительных нагрузок Nдл = 35 тс, Mдл = 35 тс·м; расчетная длина l0 = 10 м. Рис. 40. К примеру расчета 26 Требуется проверить прочность
сечения. Расчет. Расчет ведем согласно п. 3.65. Принимая fп.и = 4,91 см2 (1Æ25); pи = 2 и Σfа = 68,9 см2 (8Æ28 + 4Æ25), находим площади арматуры
Fа.и и Fа.п: Fа.и = fп.и(pи + 1) = 4,91(2 + 1) = 14,73 см2; Fа.п = Σfа/2
- Fа.и = 68,9/2 - 14,73 = 19,72 см2. Из рис. 40 имеем
a1 = 4,5 см. Тогда δ1 = a1/h = 4,5/60 = 0,075. Так как l0/h = 10/0,6 = 16,7 > 10, расчет ведем с учетом прогиба элемента,
согласно п. 3.57,
вычисляя значение Nкр по формуле (81). Для
этого определим:
e0 = M/N = 5000/50 = 100 см. Так как e0/h = 100/60 = 1,67 > tмин = 0,5 - 0,01l0/h - 0,001Rпр,
принимаем t = e0/h = 1,67. Значение
Коэффициент η равен
Определяем величины:
Из табл. 17
находим ξ0 = 0,734 и ξR = 0,572. Так как
прочность сечения проверяем из условия (102): ξ1 = ξ/ξ0 = 0,25/0,734 = 0,34; Rпрbh2[0,5ξ(1 - ξ) + αи(ξ1 - δ1)(1 - ξ1 - δ1) - 0,05αиξ12 + αп(1 - 2δ1)] = 145·40·602
[0,5·0,25(1 - 0,25) + 0,34(0,34 - 0,075)(1 - 0,34 - 0,075) - 0,05·0,34·0,342
+ 0,193(1 - 2·0,075)] = 64,4 тс·м > Ne0η =
50·1·1,11 = 55,5
тс·м, т.е. прочность сечения обеспечена. Пример
27. Дано:
размеры сечения колонны b =
60 см; h = 150 см; бетон марки М 400 (Rпр = 190 кгс/см2 с
учетом mб1 =
1,1, Eб = 3·105 кгс/см2);
арматура класса А-III (Rа = 3400 кгс/см2, Eа = 2·106 кгс/см2) расположена в
сечении, как показано на рис. 41; продольные силы и изгибающие моменты,
определенные из расчета рамы по деформированной схеме: от всех нагрузок N = 1200 тс, M = 500 тс·м; от постоянных и
длительных нагрузок Nдл = 850 тс, Mдл = 280 тс·м; расчетная длина
в плоскости изгиба l0 = 18 м, из плоскости изгиба l0 = 12 м; фактическая длина
колонны l = 12 м. Требуется проверить прочность
сечения. Рис. 41. К примеру расчета 27 Расчет
в плоскости изгиба Расчет ведем согласно п. 3.65. Принимая fп.и = 6,158 см2 (1Æ28); pи = 5 и Σfа = 174,17 см2 (14Æ32 + 10Æ28), находим площади арматуры
Fа.п и Fа.и: Fа.и = fп.и(pи + 1) = 6,158(5 + 1) = 36,95 см2; Fа.п = Σfа/2
- Fа.и = 174,17/2 - 36,95 = 50,13 см2. Центр тяжести арматуры,
расположенной у растянутой грани (7Æ32), отстоит от этой грани
на расстоянии a1 = (5·5 + 2(5 + 10))/(5 + 2) = 7,9 см. Тогда δ1 = a1/h = 7,9/150 = 0,053. Определяем величины:
Из табл. 17
находим ξ0 = 0,698 и ξR = 0,532. Так как
прочность сечения проверяем из условия (103).
Для этого вычисляем: ξ1R
= ξR/ξ0 = 0,532/0,698 = 0,762; nгр = ξR + αи(2ξ1R - 1) = 0,532 + 0,164(2·0,762
- 1) = 0,618; mгр = 0,5ξR(1 - ξR) + αи(ξ1R - δ1)(1 - ξ1R - δ1) - 0,05αиξ21R + αп(1 - 2δ1) = 0,5·0,532(1 - 0,532) +
0,164(0,762 - 0,053)(1 - 0,762 - 0,053) - 0,05·0,164·0,7622 + 0,1(1
- 2·0,053) = 0,230;
Rпрbh2mгр(nц - n1)/(nц - nгр) = 190·60·1502·0,230(1,346
- 0,702)/(1,346 - 0,618) = 523 тс·м > M = 500
тс·м, т.е. прочность сечения в плоскости изгиба обеспечена. Расчет из плоскости
изгиба Так как расчетная длина из
плоскости изгиба l0 = 12 м и отношение l0/b = 12/0,6 = 20 значительно превышает отношение l0/h = 18/1,5 = 12, соответствующее расчету колонны в плоскости изгиба,
согласно п. 3.65
следует рассчитать колонну из плоскости изгиба, принимая эксцентрицитет e0 равным случайному
эксцентрицитету e0сл. При этом за высоту сечения
принимаем его размер из плоскости изгиба, т.е. h = 60 см. Поскольку фактическая длина
колонны l = 12 м = 20h = 20·0,6 = 12 м, производим
расчет согласно п. 3.66. Площадь сечения промежуточных
стержней, расположенных по коротким сторонам, равна Fа.пр = 48,26 см2 (6Æ32). Поскольку Σfа/3 = 174,14/3 = 58 см2
> Fа.пр = 48,76 см2, в
расчете используем табл. 23 (А). Из табл. 23 и 22 при Nдл/N = 850/1200 = 0,708 и l0/h = 20 находим φж = 0,77 и φб
= 0,674. Значение α равно
По формуле (105)
определяем коэффициент φ: φ = φб + 2(φж
- φб)α = 0,674 + 2(0,77 - 0,674)0,346 = 0,74 < φж
= 0,77. Поскольку h = 60 см > 20 см,
принимаем m = 1. Проверяем условие (104): mφ(RпрF + RаΣfа)= 1·0,74(190·60·150 + 3400·174,17) = 1700 тс > N = 1200 тс, т.е. прочность сечения из плоскости изгиба
обеспечена. Пример
28. Дано:
колонна с размерами сечения 40 × 40 см; расчетная длина, равная
фактической, l = l0 = 6 м; бетон марки М 300 (Rпр = 115 кгс/см2 при
mб1 = 0,85); продольная арматура
класса А-III (Rа.с = 3400 кгс/см2);
центрально приложенные продольные силы: от постоянных и длительных нагрузок Nдл = 180 тс, от кратковременной
нагрузки Nк = 20 тс. Требуется определить площадь
сечения продольной арматуры. Расчет. Согласно п. 3.53
расчет производим с учетом случайного эксцентрицитета e0сл. Поскольку l = 6 м < 20h = 20·0,4 = 8 м, расчет
производим согласно п. 3.66. N = Nдл + Nк = 180 + 20 = 200 тс. Nдл/N = 180/200 = 0,9; l0/h = 6/0,4 = 15 и предполагая отсутствие промежуточных стержней,
находим φж = 0,858 и φб = 0,8. Поскольку h = 40 см > 20 см, m = 1. Принимая в первом приближении φ = φж, из условия (104)
находим значение RаΣfа: RаΣfа = N/(mφ) - RпрF = 200000/(1·0,858) -
115·1600 = 233 - 184 = 49 тс. Отсюда
Поскольку α < 0,5, уточняем значение φ, вычисляя его по формуле (105): φ = φб + 2(φж - φб)α = 0,8 + 2(0,858 - 0,8)0,266
= 0,831. Аналогично определяем: RаΣfа = 200000/0,831 - 115·1600 =
56,5 тс. Полученное значение RаΣfа близко к принятому в первом
приближении, поэтому суммарную площадь сечения арматуры принимаем равной: Σfа = 56500/3400 = 16,6 см2. Окончательно принимаем Σfа = 19,64 см2 (4Æ25). Прямоугольные
сечения с несимметричной арматурой Пример
29. Дано:
размеры сечения элемента b =
40 см; h = 50 см; a = a' = 4
см; бетон марки М 300 (Rпр
= 145 кгс/см2 с учетом mб1 = 1,1; Eб = 2,6·105 кгс/см2);
арматура класса А-III (Rа
= Rа.с = 3400 кгс/см2)
площадью сечения Fа = 24,63 см2 (4Æ28) и F'а = 12,32 см2 (2Æ28); продольные силы и изгибающие моменты: от постоянных и длительных
нагрузок;Nдл = 60 тс, Mдл = 16,5 тс·м; от
кратковременной нагрузки Nк =
10 тс, Mк = 19 тс·м; расчетная длина l0 = 8 м. Требуется проверить прочность
сечения. Расчет. h0 = 50 - 4 = 46 см; M = Mдл + Mк = 16,5 + 19 = 35,5 тс·м; N = Nдл + Nк = 60 + 10 = 70 тс. Так как l0/h = 8/0,5 = 16 > 10, расчет ведем с учетом прогиба элемента, согласно
п. 3.53,
вычисляя величину Nкр по формуле (81). Для
этого вычисляем:
e0 = M/N = 3550000/70000 = 50,7 см. Так как e0/h = 50,7/50 = 1,01 > tмин = 0,5 - 0,01l0/h - 0,001Rпр,
принимаем t = e0/h = 1,01. Тогда
Коэффициент η
определяем по формуле (79):
e = e0η + (h0 - a')/2 = 50,7·1,18 + (46 - 4)/2 = 80,8 см. Прочность сечения проверяем
согласно указаниям пп. 3.63 и 3.67. Вычисляем высоту сжатой зоны x по формуле (92а):
ξR
= 0,572 (см. табл. 17). Так как x = 19,3 см < ξRh0 = 0,572·46 = 26,3 см,
прочность сечения проверяется из условия (93): Rпрbx(h0 -
0,5x) + Rа.сF'а(h0 - a') = 145·40·19,3(46 -
0,5·19,3) + 3400·12,32(46 - 4) = 58,3 тс·м > Ne = 70·0,808 = 56,5 тс·м, т.е. прочность сечения обеспечена. Пример
30. Дано:
размеры сечения элемента b =
40 см; h = 50 см; a = a' = 4
см; бетон марки М 300 (Rпр
= 115 кгс/см2 с учетом mб1 = 0,85; Eб = 2,6·105 кгс/см2);
арматура класса А-III (Rа = Rа.с = 3400 кгс/см2);
продольная сила N = 80 тс, ее эксцентрицитет
относительно центра тяжести бетонного сечения, определенный из статического
расчета по недеформированной схеме, e0 =
50 см; расчетная
длина l0 = 4,8 см. Требуется определить площади
сечения арматуры A и A'. Расчет. h0 = 50 - 4 = 46 см. Так как 4 < l0/h = 4,8/0,5 = 9,6 < 10, расчет ведем с учетом прогиба элемента,
согласно п. 3.53,
принимая значение Nкр равным Nкр = 0,15EбF/(l0/h)2
= 0,15·2,6·105·40·50/9,62 = 846 тс. Коэффициент η вычисляем
по формуле (79):
Значение e, с учетом прогиба элемента, равно: e = e0η + (h0
- a')/2 = 50·1,104 + (46 - 4)/2 =
76,2 см. Требуемую площадь сечения
арматуры A и A' определяем по формулам (106) и (107):
Принимаем: F'а =
16,09 см2
(2Æ32); Fа = 28,4 см2 (2Æ36 + 1Æ32). Двутавровые
сечения Пример 31. Дано: размеры сечения и расположение арматуры - по рис. 42; бетон марки М 400 (Eб = 3·105 кгс/см2, Rпр =
190 кгс/см2 с учетом mб1 = 1,1); арматура класса А-III (Rа = Rа.с = 3400 кгс/см2)
площадью поперечного сечения Fа = F'а = 56,3 см2 (7Æ32); продольные силы и
изгибающие моменты: от постоянных и длительных нагрузок Nдл = 200 тс, Mдл = 246 тс·м, от всех нагрузок
N = 250 тс, M = 370 тс·м, расчетные длины элемента: в плоскости изгиба - l0 = 16,2 м, из плоскости изгиба l0 = 10,8 м; фактическая длина
элемента l = 10,8 м. Требуется проверить прочность
сечения. Рис. 42. К примерам расчета 31, 32
и 37 Расчет в
плоскости изгиба Принимаем расчетную толщину
полки h'п равной средней высоте свесов h'п = hп = 20 + 3/2 = 21,5 см. Вычисляем площадь и момент
инерции бетонного сечения: F = 20·150 + 2·40·21,5 = 4720 см2;
Радиус инерции сечения равен
Так как l0/r = 1620/52 = 31,1 < 35, но больше 14, расчет ведем с учетом прогиба
элемента, согласно п. 3.57, принимая значение Nкр равным
Коэффициент η определяем
по формуле (79):
Центр тяжести площади
арматуры Fа и F'а отстоят от ближайшей грани на
расстоянии a = a' = (5·5 + 2·15)/(5 + 2) = 7,9 см. откуда h0 = h - a = 150 -
7,9 = 142,1 см. Значение e с учетом прогиба элемента равно e = e0η + (h0
- a')/2 = (37000/250)1,093 + (142,1 -
7,9)/2 = 228,9 см. Проверяем условие (114): Rпрb'пh'п = 190·60·21,5 = 245,1 тс
< N = 250 тс, т.е. расчет ведем как для двутаврового сечения. Площадь сжатых свесов полки
равна Fсв =
(b'п -
b)h'п = (60 - 20)21,5 = 860 см2. Определяем высоту сжатой
зоны:
Из табл. 17
находим ξR
= 0,532. Так как x = 22,8 см < ξR/h0 = 0,532·142,1 = 75,6 см, прочность сечения проверяем
из условия (115): Rпрbх(h0 - x/2)
+ RпрFсв(h0 - hп'/2) + Rа.сF'а(h0 - a') = 190·20·22,8(142,1
- 22,8/2) + 190·860(142,1 - 21,5/2) + 3400·56,3(142,1 - 7,9) = 584,7 тс·м
> Ne = 250·2,29 = 572,5 тс·м, т.е. прочность сечения в плоскости изгиба обеспечена. Расчет из
плоскости изгиба Определяем радиус инерции из
плоскости изгиба.
Так как гибкость из плоскости
изгиба l0/r = 1070/13,4 = 80 значительно превышает гибкость в плоскости изгиба l0/r = 31,1, согласно п. 3.54, проверяем прочность сечения из плоскости изгиба,
принимая эксцентрицитет e0 равным случайному
эксцентрицитету e0сл. Высота сечения при этом
равна h = 60 см. Поскольку
фактическая длина колонны l =
10,8 м < 20h = 20·0,6 = 12 м, расчет
можно производить, согласно п. 3.66, как для прямоугольного сечения, не учитывая
«в запас» сечение ребра, т.е. принимая b = 2·21,5 = 43 см. Площадь сечения промежуточных
стержней, расположенных вдоль обеих полок, равна Fа.пр = 48,26 см2 (6Æ32), а площадь сечения всех стержней Σfа = 112,6 см2. Поскольку Σfа/3 = 112,6/3 = 37,5 см2 < Fа.пр = 48,26 см2, в расчете используем табл. 23 (Б).
Из табл. 23
при Nдл/N = 200/250 = 0,8 и l0/h = 10,8/0,6 = 18 находим φж = 0,724. Значение α
равно
Следовательно, φ = φж = 0,724. Поскольку h = 60 см > 20 см,
принимаем m = 1. Проверяем условие (104): mφ(RпрF + Rа.сΣfа) = 1·0,724(190·43·60 +
3400·112,6) = 632 тс > N = 250
тс, т.е. прочность сечения из плоскости изгиба
обеспечена. Пример
32. Дано:
размеры сечения и расположение арматуры - по рис. 42; бетон марки М 400 (Rпр = 190 кгс/см2 с
учетом mб1 = 1,1; Eб = 3·105 кгс/см2);
арматура симметричная класса А-III (Rа = Rа.с = 3400 кгс/см2);
продольная сила N = 600 тс, изгибающий момент M = 310 тс·м; расчетная длина
элемента в плоскости изгиба l0 = 16,2 м, из плоскости
изгиба l0 = 10,8 м. Требуется определить площадь
сечения арматуры. Расчет в плоскости
изгиба Из примера 31 имеем:
h'п = 21,5 см; h0 = 142,1 см; a' =
7,9 см; Nкр = 2924 тс. По формуле (79)
определяем коэффициент η
Значение e, с учетом прогиба элемента, равно e = e0η +
(h0 - a')/2
= (M/N)η + (h0 - a')/2
= (31000/600)1,26 + (142,1 - 7,9)/2 = 132,1 см. Проверяем условие (114): Rпрb'пh'п = 190·60·21,5 = 245,1 тс
< N = 600 тс, т.е. расчет ведем как для двутаврового сечения. Площадь сжатых свесов полки
равна Fсв =
(b'п -
b)h'п = (60 - 20)21,5 = 860 см2. Определяем значения
δ = a'/h0 =
7,9/142,1 = 0,055;
Из табл. 17
находим ξR = 0,532. Так как ξ =
Из табл. 17
находим s = 3,22 и ξ0 = 0,698.
Отсюда
Принимаем Fа = 56,3 см2 (7Æ32). Расчет из плоскости изгиба
производим аналогично примеру 31. Кольцевые сечения Пример
33. Дано:
внутренний радиус сечения r1 = 15 см; наружный радиус r2
= 25 см; бетон марки М 300 (Rпр = 145 кгс/см2 при mб1 = 1,1); продольная арматура класса А-III (Rа = Rа.с = 3400 кгс/см2)
площадью сечения Fа.к = 14,7 см2 (13Æ12); продольная сила от полной нагрузки N = 120 тс, ее эксцентрицитет относительно центра тяжести сечения, с
учетом прогиба элемента, равен e0 =
12 см. Требуется проверить прочность
сечения. Расчет. Вычисляем площадь кольцевого
сечения: F = π(r22 - r12) = 3,14(252 - 152)
= 1256 см2. Относительная площадь сжатой
зоны бетона равна
rа = rср = (r1 + r2)/2 = (15 + 25)/2 = 20 см. Так как 0,15 < αк = 0,536 < 0,6, прочность
сечения проверяем из условия (122): Ne0 = 120·0,12 = 14,4 тс·м
< (RпрFrср + RаFа.кrа) т.е. прочность сечения обеспечена. Круглые
сечения Пример 34. Дано: диаметр сечения D = 40 см; a = 3,5 см; расчетная длина l0 = 4 м; бетон марки М 300 (Rпр = 115 кгс/см2 при mб1 = 0,85; Eб = 2,6·105 кгс/см2); продольная арматура класса А-III (Rа = Rа.с = 3400 кгс/см2) площадью сечения Fа.к = 31,4 см2 (10Æ20); продольные силы и
изгибающие моменты: от постоянных и длительных нагрузок Nдл = 40 тс, Mдл = 10 тс·м; от всех нагрузок N = 60 тс, M = 14 тс·м. Требуется проверить прочность
сечения. Расчет. Вычисляем площадь круглого
сечения: F = πD2/4 = 3,14·402/4
= 1256 см2. Радиус инерции сечения rи = D/4 = 40/4 = 10 см. Гибкость элемента l/rи = 400/10 = 40 > 14, следовательно, расчет производим с учетом влияния
прогиба элемента, согласно п. 3.57, а значение Nкр определяем по формуле (80). Для этого вычисляем: rа = D/2 - a = 40/2 - 3,5 = 16,5 см;
e0 = M/N = 1400/60 = 23,3 см. Так как e0/D = 23,3/40 = 0,583 > tмин = 0,5 - 0,01l0/D - 0,001Rпр, принимаем t = e0/D = 0,583. Моменты инерции бетонного сечения и всей арматуры
соответственно равны: I = πD4/64 = 3,14·404/64 = 125600 см4; Iа = Fа.кrа2/2 = 31,4·16,52/2 = 4274 см4; n = Eа/Eб = 2·106/2,6·105 = 7,69. Тогда
Коэффициент η определяем по формуле (79):
Прочность сечения проверим с
помощью графика на рис. 35. По значениям n1 = N/(RпрF) = 60000/(115·1256) =
0,415;
на графике находим A0кр = 0,55. Поскольку A0крRпрFr = 0,55·115·1256·20 = 15,9
тс·м > Ne0η = 60·0,233·1,124 = 15,7 тс·м, то прочность сечения обеспечена. Пример
35. По
данным примера 34
подобрать необходимое количество продольной арматуры, пользуясь графиком на
рис. 35. Расчет. Из примера 34 имеем: rи = 10 см; F =
1256 см2. Поскольку l0/rи = 400/10 = 40 > 35, арматуру подбираем с учетом
влияния прогиба элемента, вычисляя значение Nкр по формуле (80). В первом приближении
принимаем Fа.к = 0,01F = 12,56 см2, откуда Iа = Fа.кrа2/2 = 12,56·16,52/2 =
1710 см4 (rа = D/2 - a = 20 - 3,5 = 16,5 см). Из примера 34 имеем:
kдл = 1,695; t = 0,583; l = 125600 см4. Тогда
Значение коэффициента η
равно
По значениям
и a/D = 3,5/40 ≈ 0,1 на
графике рис. 35
находим α = 0,9. Откуда Fа.к = αRпрF/Rа = 0,9·115·1256/3400 = 38,23 см2. Поскольку полученное
армирование существенно превышает принятое в первом приближении (Fа.к = 12,56 см2),
значение Fа.к = 38,23 см2 определено с запасом и его
можно несколько уменьшить, уточнив значение Nкр. Принимаем Fа.к = (12,56 + 38,23)/2 = 25,4
см2 и снова проведем аналогичный расчет: Iа = 25,4·16,52/2 = 3457 см4; Nкр = 10,4(19350 + 7,69·3457) =
478 тс;
По значениям A0кр = 0,589·1,144/1,217 = 0,554;
n1 = 0,415 и a/D = 0,1 на графике рис. 35
находим α = 0,81; Fа.к = 0,81·115·1256/3400 = 34,4
см2. Принимаем Fа.к = 34,6 см2 (11Æ20). Расчет элементов,
работающих на косое внецентренное сжатие Пример
36. Дано: размеры
прямоугольного сечения колонны b =
40 см; h =
60 см; бетон марки М 300 (Rпр
= 145 кгс/см2 при учете mб1 = 1,1); продольная арматура
класса А-III (Rа = Rа.с = 3400 кгс/см2)
расположена в сечении согласно рис. 43; в сечении одновременно
действуют продольная сила N =
260 тс и изгибающие моменты в плоскости, параллельной размеру h, - Mх = 24 тс·м и в плоскости,
параллельной размеру b, -
Mу = 18,25 тс·м; моменты Mх и Mу даны с учетом прогиба
колонны. Требуется проверить прочность
сечения. Расчет. Проверку прочности
производим согласно п. 3.76. Ось симметрии, параллельную
размеру h, обозначим x, а другую ось симметрии - y. Определим предельные моменты Mх0 и Mу0. Для этого вычисляем
распределенное армирование Fах и Fау. Из рис. 43
имеем: fпх = 0; pх = 0; f0 = 8,043 см2 (Æ32); fпу = 3,142 см2 (Æ20); Рис. 43. К примеру расчета 36 и 38 I - граница сжатой зоны в первом приближении; II - окончательная
граница сжатой зоны
Fах = fпх(pх + 1) + (2f0
- fпх - fпу)B/(1 + B) = (2·8,043 - 3,142)0,877/(1 + 0,877) = 6,05 см2; Σfа = 38,45 см2 (4Æ32 + 2Æ20); Fау = Σfа/2 - Fах = 38,45/2 - 6,05 = 13,18 см2. При определении, согласно п. 3.65,
момента Mх0, действующего в плоскости оси x, принимаем: Fа.и = Fау = 13,18 см2; Fа.п = Fах = 6,05 см2; h = 60 см; b = 40 см; δ1 = a1/h = 5/60 = 0,083; Rпрbh = 145·40·60 = 348000 кгс;
Из табл. 17
находим ξ0 = 0,734 ξR = 0,572. Так как
значение Mх0 определяем по формуле (102),
вычислив ξ1 = ξ/ξ0 = 0,573/0,734 = 0,781; Mх0 = Rпрbh2[0,5ξ(1 - ξ) + αи(ξ1 - δ1)(1 - ξ1 - δ1) - 0,05αиξ12 + αп(1 - 2δ1)] = 348000·60[0,5·0,573(1 -
0,573) + 0,309(0,781 - 0,083)(1 - 0,781 - 0,083) - 0,05·0,309·0,7812
+ 0,06(1 - 2·0,083)] = 40,1 тс·м. При определении момента Mу0, действующего в плоскости оси y, принимаем: Fа.и = Fах = 6,05 см2; Fа.п = Fау = 13,18 см2; h = 40 см; b = 60 см; δ1 = a1/h = 5/40 = 0,125;
Так как значение Mу0 определяем по формуле (103),
вычислив:
ξ1R = ξR/ξ0
= 0,572/0,734 = 0,78; mгр = 0,5ξR(1 - ξR) + αи(ξ1R - δ1)(1 - ξ1R - δ1)
- 0,05αиξ21R + αп(1 - 2δ1) = 0,5·0,572(1 - 0,572)
+ 0,158(0,78 - 0,125)(1 - 0,78 - 0,125) - 0,05·0,158·0,782 + 0,129(1
- 2·0,125) = 0,224; nгр = ξR + αи(2ξ1R - 1) = 0,572 + 0,158(2·0,78 - 1) = 0,66;
Поскольку Пример
37. Дано:
сечение колонны, характеристики материалов и значение продольной силы от всех
нагрузок по примеру 31; в сечении одновременно действуют изгибающие
моменты в плоскости, параллельной размеру h, - Mх = 333 тс·м и в плоскости,
параллельной размеру b, -
Mу = 39,6 тс·м; моменты Mх и Mу даны с учетом прогиба
колонны. Требуется проверить прочность
сечения. Расчет. Проверку прочности
производим согласно п. 3.77. Определим предельный момент Mх0, действующий в плоскости оси
симметрии x, проходящей
в ребре. Согласно примеру 31, правая часть условия (115) п. 3.69
равна 584,7 тс·м. Тогда Mх0 = 584,7 - N(h0 - a')/2 = 584,7 - 250(1,421 -
0,079)/2 = 417 тс·м. Предельный момент Mу0, действующий в плоскости оси симметрии y, нормальной ребру, определяем как для прямоугольного сечения,
составленного из двух полок, согласно п. 3.65. Тогда, согласно рис. 42,
имеем: h = 60 см; b = 2·21,5 = 43 см. Определим распределенное
армирование Fа.и и Fа.м; fп.и = 8,043 см2 (Æ32); pи = 3; Σfа = 112,6 см2 (14Æ32); Fа.и =
fп.и(pи + 1) = 8,043(3 + 1) = 32,2
см2; Fа.п =
Σfа/2 - Fа.и = 112,6/2 - 32,2 = 24,1 см2. Из табл. 17
находим ξ0 = 0,698 и ξR= 0,532. Определяем величины: Rпрbh = 190·43·60 = 490200 кгс; δ1 = a1/h
= 0,083;
Значение Mу0 определяем по формуле (102): ξ1 = ξ/ξ0 = 0,412/0,698 = 0,59; Mу0 = Rпрbh2[0,5ξ(1 - ξ) + αи(ξ1 - δ1)(1 - ξ1 - δ1) - 0,05αиξ12 + αп(1 - 2δ1)] = 190·43·602[0,5·0,412·(1
- 0,412) + 0,536(0,59 - 0,083)(1 - 0,59 - 0,083) - 0,05·0,536·0,592
+ 0,167(1 - 2·0,083)] = 100,0 тс·м. Проверяем прочность сечения,
принимая b = 20 см, h = 150 см. Поскольку Пример
38. Дано:
размеры прямоугольного сечения колонны b = 40 см; h = 60 см; бетон марки М 300 (Rпр = 145 кгс/см2,
при учете mб1 = 1,1); продольная арматура
класса А-III (Rа =
3400 кгс/см2)
- по рис. 43,
в сечении одновременно действуют продольная сила N = 260 тс и изгибающие моменты в плоскости, параллельной размеру h, - Mх =
25 тс·м и в плоскости, параллельной
размеру b, - Mу = 20 тс·м; изгибающие моменты Mх и Mу даны с учетом прогиба
колонны. Требуется проверить прочность
сечения, пользуясь формулами общего случая расчета п. 3.78. Расчет. Все стержни обозначим
номерами, как показано на рис. 43. Через центр тяжести наиболее растянутого
стержня (№ 5) проводим ось x
параллельно размеру h =
60 см и ось y параллельно размеру b. Угол γ между осью y и прямой, ограничивающей сжатую зону, принимаем как при расчете
упругого тела на косое внецентренное сжатие, т.е.
Задаваясь значением x1 - размером сжатой зоны по
наиболее сжатой стороне сечения h, можно определить для каждого
стержня отношение ξi
= x/h0i
по формуле ξi = x1/(aуitgγ +
aхi), где aхi
и aуi -
расстояния от i-го стержня до наиболее
сжатой стороны сечения в направлении соответственно осей x и y. По значениям ξi определяем напряжение σаi, принимая σε
= 4000, ξ0 = 0,734 (см. табл. 17):
При этом если σаi > Rа = 3400 кгс/см2,
что равносильно условию ξi < ξR = 0,572 (см. табл. 17), принимаем σаi = Rа = 3400 кгс/см2.
Если σаi
< -Rа.с = -3400 кгс/см2,
принимаем σаi
= -3400 кгс/см2. Последнее условие после подстановки в него
выражения для σаi
приобретает вид: ξi >
0,734/(1 - 3400/12000)
= 1,023. Затем определяем сумму усилий
во всех стержнях Σfаiσаi. Задаваясь в
первом приближении значением x1 = h = 60 см, производим
указанные вычисления, результаты которых приводим в таблице.
Так как x1/tgγ =
60/1,8 = 33,3 см < b = 40 см,
форма сжатой зоны треугольная, ее площадь равна
Проверим равенство (138). RпрFб -
Σfаiσаi = 145·1000 + 42670 = 187670
кгс < N = 260000 кгс, т.е. сжатая зона занижена. Увеличиваем значение x1 до 70 см и аналогично определяем Σfаiσаi (см. табл.). При x1 > h и x1/tgγ = 70/1,8 = 38,9 см < b = 40 см форма сжатой зоны трапециевидная и площадь ее равна
Поскольку RпрFб -
Σfаiσаi = 145·1337 + 70680 = 264580
кгс ≈ N = 260000
кгс, равенство (138) приблизительно
соблюдается. Определим моменты внутренних
сил относительно осей y и
x. Для этого определим
статические моменты сжатой зоны относительно этих осей:
Тогда: Mхпр = RпрSбх - Σfаiσаi(aх5 - aхi) = 145·43370
- [-27350(55 - 5)2 - 940(55 - 30) - 10690(55 - 30)] = 9310000 кгс·см; Mупр = RпрSбу - Σfаiσаi(aу5 - aуi) = 145·29030
- [-27350(35 - 5)2 - 10690(35 - 5)] = 6172000 кгс·см. Моменты внешних сил
относительно осей y и x равны: Mх1 = Mх + N(h/2 - 0,05) = 25 + 260(0,6/2 - 0,05) = 90 тс·м; Mу1 = Mу +
N(b/2 - 0,05) = 20 + 260(0,4/2 -
0,05) = 59 тс·м. Поскольку Mхпр > Mх1, а Mупр > Mу1,
прочность сечения обеспечена. Центрально- и
внецентренно-растянутые элементы
Центрально-растянутые элементы
3.79(3.26). При расчете сечений
центрально-растянутых железобетонных элементов должно соблюдаться условие N ≤ RаFа, (140) где Fа - площадь сечения всей продольной арматуры. Внецентренно-растянутые элементы
Расчет прямоугольных сечений, нормальных к продольной оси элемента, при
расположении продольной силы в плоскости оси симметрии
3.80(3.27). Расчет прямоугольных сечений внецентренно-растянутых элементов с
арматурой, сосредоточенной у наиболее растянутой и у сжатой (наименее
растянутой) граней, должен производиться в зависимости от положения продольной
силы N: а) если продольная сила N приложена между равнодействующими усилий в арматуре A и A' (рис. 44,а), т.е. при e' ≤ h0 - a', -
из условий Ne' ≤ RаFа(h'0 - a') (141) и Ne ≤ RаF'а(h0 - а'); (142) Рис. 44. Схема усилий и эпюра
напряжений в сечении, нормальном к продольной оси внецентренно-растянутого
железобетонного элемента при расчете его по прочности а - продольная сила N приложена
между равнодействующими усилий в арматуре A и A'; б - то же, за пределами расстояния между
равнодействующими усилий в арматуре A и A' б) если продольная сила N приложена за пределами расстояния
между равнодействующими усилий в арматуре A и A'
(рис. 44,б),
т.е. при e' > h0 - a', - из условия Ne
≤ Rпрbx(h0 - 0,5x) + Rа.сF'а(h0 - a'), (143) при этом высота сжатой зоны x определяется по формуле Если полученная из расчета по
формуле (144)
величина x > ξRh0, в условие (143)
подставляется значение x = ξRh0, где ξR определяется
по табл. 17
п. 3.15. Если x < 0, то прочность сечения
проверяется из условия (141). При симметричном армировании
прочность независимо от значения e' проверяется из условия (141). Примечание.
Если при e' >
h0 - a' высота
сжатой зоны, определенная без учета сжатой арматуры 3.81. Определение требуемого количества продольной арматуры производится
следующим образом: а) при e' ≤ h0 - a' площадь сечения арматуры A и A' определяется соответственно
по формулам и
б) при e' > h0 - a' площадь сечения растянутой
арматуры определяется по формуле где ξ -
определяется по табл. 18 п. 3.19 в зависимости от значения
При этом должно
удовлетворяться условие A0 ≤ AR (см. табл. 17 п. 3.15). В
противном случае следует увеличить сечение сжатой арматуры F'а, повысить марку бетона или
увеличить размеры сечения. Если A0 < 0 площадь сечения
растянутой арматуры определяется по формуле (145). Подбор симметричного
армирования независимо от значения e' производится по формуле (145). Примечание. При e' >
h0 - a' необходимое количество арматуры, определенное
по формуле (145),
можно несколько снизить, если значение ξ, определенное по табл. 18 без учета сжатой арматуры, т.е. по значению где υ -
определяется по табл. 18 в зависимости от
Общий случай расчета
нормальных сечений внецентренно-растянутого элемента (при любых сечениях,
внешних усилиях и любом армировании)
3.82(3.28). Расчет сечений внецентренно-растянутого элемента в общем случае (рис. 39) должен производиться из
условия N где Sб - статический момент площади сжатой зоны бетона
относительно указанной оси; Sаi - статический момент площади сечения i-го стержня продольной
арматуры относительно указанной оси; σаi - напряжение в i-м
стержне продольной арматуры. Высота сжатой зоны x и напряжения σаi определяются из совместного
решения уравнений (138) и (139) п. 3.78 с
заменой перед N знака
минус на знак плюс. При косом внецентренном
растяжении для определения положения границы сжатой зоны кроме использования
формул (138)
и (139)
требуется соблюдение дополнительного условия, чтобы точки приложения внешней
продольной силы, равнодействующей сжимающих усилий в бетоне и арматуре и
равнодействующей усилий в растянутой арматуре, лежали на одной прямой (рис. 39). Расчет сечений, наклонных к продольной оси
элемента
3.83(3.33). Расчет наклонных сечений
внецентренно-растянутых элементов на действие поперечной силы производится, как
и для изгибаемых элементов, согласно пп. 3.30 - 3.44; при этом значения Rр во всех этих пунктах
умножаются на коэффициент kN, равный но принимаемый не менее 0,2. Расчет наклонных сечений
внецентренно-растянутых элементов на действие изгибающего момента производится,
как и для изгибаемых элементов, согласно пп. 3.45 - 3.50. При этом высота сжатой зоны в наклонном
сечении определяется с учетом растягивающей силы N по формуле (144) п. 3.80 или
согласно п. 3.82.
В случае выполнения условия e'
< h0 - a' расчетный момент в наклонном
сечении допускается определять как момент всех внешних сил, расположенных по
одну сторону от рассматриваемого наклонного сечения, относительно оси,
проходящей через центр тяжести арматуры A'. Примеры
расчета
Внецентренно-растянутые
элементы Пример
39. Дано:
растянутая ветвь у двухветвевой колонны с размерами поперечного сечения b = 50 см; h = 20 см; a = a' = 4
см; продольная арматура класса А-III (Rа = Rа.с = 3400 кгс/см2)
площадью сечения Fа = F'а = 9,82 см2 (2Æ25); бетон марки М 300 (Rпр = 145 кгс/см2 при
mб1 = 1,1); продольная растягивающая
сила N = 4,4 тс; максимальный
изгибающий момент M =
4,3 тс·м. Требуется проверить прочность
нормального сечения. Расчет. h0 = 20 - 4 = 16 см; e0 = M/N = 4,3/4,4 = 0,977 м; e' = e0 + h/2 - a'= 0,977 + 0,2/2 - 0,04 = 1,037 м; e = e0 - h/2 + a = 0,977 - 0,2/2 +
0,04 = 0,917 м. Поскольку арматура
симметричная, прочность проверяем из условия (141) RаFа(h0 - a') = 3400·9,82(16 - 4) =
401000 кгс·см < Ne' = 4,4·1,037 = 4,56 тс·м,
т.е. условие (141)
не удовлетворяется. Так как e' = 1,037 м > h0 - a' =
12 см, а высота сжатой зоны x,
определенная без учета сжатой арматуры:
согласно примечанию к п. 3.80 проверим прочность из
условия (143),
принимая x = 4 см и F'а = 0: Rпрbx(h0 - 0,5x) =
145·50·4(16 - 0,5·4) = 406000 кгс·см = 4,06 тс·м > Ne = 4,4·0,917 = 4,04 тс·м, т.е. прочность нормального сечения обеспечена. Пример
40. Дано:
размеры сечения b = 100 см; h = 20 см; a = 3,5 см; бетон марки М 200
(Rпр = 75 кгс/см2 при mб = 0,85); продольная арматура
класса А-III (Rа = Rа.с = 3400 кгс/см2). Площадь сечения арматуры A' - Fа = 10,05 см2;
растягивающая сила N =
16 тс; изгибающий момент M =
11,6 тс·м. Требуется определить площадь
сечения арматуры A. Расчет. h0 = h - a = 20 - 3,5 = 16,5 см; e0 = M/N = 11,6/16 = 0,725 м; e = e0 - h/2 + a= 0,725 - 0,2/2 +
0,035 = 0,66 м; e' = e0 + h/2 - a' = 0,725 + 0,2/2 - 0,035 = 0,79 м. Так как e' =
79 см > h0 - a' = 16,5 - 3,5 = 13 см,
определим необходимую площадь сечения растянутой арматуры согласно п. 3.81
«б». Вычисляем значение
Так как 0 < A0 < AR = 0,443 (см. табл. 17),
значение Fа определяем по формуле (147).
Для этого по табл. 18 при A0 = 0,3 находим ξ =
0,367.
Принимаем Fа = 30,79 см (5Æ28). Пример
41. Дано:
размеры сечения b = 100 см; h = 20 см; a = a' = 4
см; бетон марки М 200 (Rпр = 75 кгс/см2 при mб1 = 0,85); продольная арматура
класса А-III (Rа = Rа.с = 3400 кгс/см2);
растягивающая сила N =
53,2 тс; изгибающий момент M =
7,4 тс·м. Требуется определить площадь
сечения симметричной продольной арматуры. Расчет. h0 = h - a = 20 - 4 = 16 см; e0 = M/N = 7,4/53,2 = 0,139 м; e = e0 - h/2 + a = 0,139 - 0,2/2 +
0,04 = 0,079 м; e' = e0 + h/2 - a'= 0,139 + 0,2/2 - 0,04 = 0,199 м. Поскольку арматура
симметричная, площадь сечения арматуры определяем по формуле (145):
Так как e' =
19,9 см > h0 - a' =
12 см, согласно примечанию к п. 3.81, значение Fа можно уточнить. Определяем значение ξ
без учета сжатой арматуры. Для этого вычисляем значение A0
Из табл. 18 при A0 = 0,219 находим ξ =
0,25 и υ = 0,875; так как ξ
= 0,25 < 2a'/h0 = 2·4/16 = 0,5, определяем значение Fа по формуле (149):
Принимаем Fа = 24,54 см2 (5Æ25). Пример
42. Дано:
растянутая ветвь двухветвевой колонны с размерами сечения b = 50 см; h = 20 см; a = a' = 4
см; бетон марки М 300 (Rр = 11 кгс/см2 при mб1 = 1,1); хомуты,
расположенные по граням ветви, из арматуры класса А-III (Rа.х = 2700
кгс/см2); продольная растягивающая сила N = 4,4 тс, поперечная сила Q =
14,3 тс, расстояние между перемычками двухветвевой колонны 60 см. Требуется определить диаметр
и шаг хомутов. Расчет. h0 = 20 - 4 = 16 см. По формуле (151)
определим коэффициент kN
Тогда учитываемое в расчете
расчетное сопротивление бетона растяжению будет равно: Rр = 11·0,9 = 9,9 кгс/см2. Проверяем условие (47) п. 3.31: 0,6Rрbh0 = 0,6·9,9·50,16 = 4750 кгс
< Q = 14,3 тс, следовательно, хомуты подбираем из расчета по
прочности. Необходимую интенсивность хомутов определяем по формуле (56):
По формуле (55)
определяем значение c0:
т.е. длина проекции невыгоднейшего наклонного сечения
не выходит за пределы расстояния между перемычками. Максимально допустимый шаг
хомутов, согласно п. 3.33, равен
Кроме того, шаг хомутов,
согласно п. 5.58,
не должен превышать 2h =
2·20 = 40 см. Принимаем шаг хомутов u = 10 см < uмакс. Из формулы (54)
определяем значение Fх
принимаем два хомута диаметром по 8 мм (Fх = 1,01 см2). Элементы, работающие
на кручение с изгибом
Элементы
прямоугольного сечения
3.84(3.42). При расчете элементов на
кручение с изгибом должно
соблюдаться условие Mк ≤ 0,1Rпрb2h, (152) где b и h - соответственно меньший и
больший размеры граней элемента. При этом значение Rпр для бетонов проектных марок
выше М 400 принимается как для бетона марки М 400. 3.85(3.38). Для участков элемента, в которых Mк > 0,5Qb (где b - размер грани, перпендикулярной к плоскости действия изгибающего
момента), следует производить расчет пространственных сечений согласно пп. 3.86 - 3.90. Для участков элемента, в
которых Mк ≤ 0,5Qb, следует производить расчет
сечений, наклонных к продольной оси элемента, на действие поперечной силы и
крутящего момента из условия Q ≤ Qх.б - 3Mк/b, (153) где Q и Mк - принимаются
наибольшими на рассматриваемом участке элемента; Qх.б - определяется по формуле (53) п. 3.35. При этом расчет наклонных и
нормальных сечений на действие изгибающего момента производится без учета
кручения. Если удовлетворяется условие Mк ≤0,25Qb, (154) то при наличии отогнутых стержней в правую часть
условия (153) добавляется величина
ΣRа.хFоsinα
(см. п. 3.32). Общий случай расчета пространственного
сечения
3.86(3.43). При расчете пространственного сечения (рис. 45) по прочности проверяется
достаточность продольной и поперечной арматуры, установленной у грани элемента,
противоположной сжатой зоне пространственного сечения. Рассматриваются три
возможные расчетные схемы расположения сжатой зоны пространственного сечения: 1-я схема - у сжатой от изгиба грани элемента (рис. 46,а); 2-я схема - у грани элемента,
параллельной плоскости действия изгибающего момента (рис. 46,б); 3-я схема - у растянутой от изгиба грани элемента (рис.
46,в). Рис. 45. Схема усилий в
пространственном сечении железобетонного элемента Рис. 46. Расчетные схемы
расположения сжатой зоны пространственного сечения а -
у сжатой от изгиба грани элемента; б - у грани элемента, параллельной плоскости действия изгибающего
момента; в - у растянутой от изгиба грани элемента; 1 - плоскость
действия изгибающего момента Для любой из этих схем расчет
пространственного сечения производится из условия Высота сжатой зоны x определяется по формуле При этом если x < 2a', в условии (155)
принимается x = 2a'. Если x > ξRh0 (где ξR - см. п. 3.15),
должна быть проверена прочность нормального сечения согласно п. 3.16. В формулах (155) и
(156),
а также в остальных формулах настоящего пункта: Fа и F'а - площадь сечения продольной арматуры, расположенной
при данной расчетной схеме соответственно в растянутой и в сжатой зонах; b и h - размеры граней элемента,
соответственно параллельных и перпендикулярных линии, ограничивающей сжатую
зону;
β = c/b; (158) c - длина проекции линии, ограничивающей сжатую зону,
на продольную ось элемента; невыгоднейшее значение c в общем
случае определяется последовательными приближениями и принимается не более 2h +
b и не более длины участка
элемента, на котором учитываемые в расчете усилия (M, Mк, Q) не меняют знаки. Для некоторых частных случаев значение c определяется согласно пп. 3.89 и 3.90. В формуле (155), а
также (160)
и (161)
величины χ и k, характеризующие соотношения
между действующими усилиями Mк, M и Q,
принимаются: при расчете по 1-й схеме χ = M/Mк и k =
1; при расчете по 2-й схеме χ = 0 и k = 1 + Qh/(2Mк); при расчете по 3-й схеме χ = -M/Mк и k =
1. Крутящий момент Mк, изгибающий момент M и поперечная сила Q принимаются
в поперечном сечении, проходящем через центр тяжести сжатой зоны
пространственного сечения (рис. 47). Значение коэффициента γ, характеризующего соотношение
между поперечной и продольной арматурой, определяется по формуле где fх - площадь сечения одного стержня хомута, расположенного у грани,
являющейся для рассматриваемой расчетной схемы растянутой; u -
расстояние между указанными выше хомутами. При этом значение γ принимается не менее и не более Рис. 47. Определение
действующих в пространственном сечении изгибающего и крутящего моментов, а
также поперечной силы при расчете на прочность железобетонного элемента,
работающего на кручение с изгибом а - при 1-й и 3-й схемах; б - при 2-й схеме; 1 - сжатая
зона пространственного сечения Если значение γ, подсчитанное по формуле (159),
получается менее γмин, то величина RаFа, вводимая в формулу (155),
умножается на отношение γ/γмин.
Допускается в этом случае значение x не
корректировать. Расчет по 3-й схеме не
производится, если удовлетворяется условие M > Mк/(2 Упрощенные способы расчета
пространственного сечения
3.87. Необходимую из расчета по 2-й схеме интенсивность поперечной арматуры fх/u, расположенной у грани, параллельной плоскости изгиба (шириной h, см. рис. 48), допускается определять по
формуле где значение γ принимается равным но не менее A/ Здесь
Mк и Q - максимальные значения крутящего момента и поперечной силы на
рассматриваемом участке; Fа2 - площадь сечения всех продольных стержней, расположенных у грани
элемента шириной h (параллельной плоскости
изгиба); a2 - см. рис. 48. Рис. 48. Обозначения,
принятые при упрощенном способе расчета на кручение с изгибом элементов
прямоугольного сечения согласно п. 3.87 1 - плоскость действия изгибающего момента При этом должно
удовлетворяться условие Если это условие не
выполняется, то следует увеличить арматуру Fа2 или размер b. Если усилия Mк и Q линейно уменьшаются от опоры к пролету, значение γ в формуле (164) рекомендуется определять
с учетом разгружающего влияния внешней нагрузки по формуле и принимать не менее
где
mк, p - уменьшение усилий Mк и Q на
единице длины элемента. В этом случае условие (165)
заменяется условием 3.88. Для элементов, в которых изгибающий момент уменьшается от опоры к пролету
(опорные зоны неразрезных балок, консоли), проверку прочности по продольной и
поперечной арматуре, расположенной у растянутой от изгиба грани элемента
шириной b (1-я расчетная схема), допускается производить из условий: M0 ≤ k1RаFа(h0 - 0,5x); (168) Mк ≤ k2Rа.хfх где Fа, fх, b, h0, x - значения, соответствующие 1-й
расчетной схеме согласно рис. 46,а;
значение x определяется по формуле (156) п.
3.86; M0 и Mк - изгибающий и крутящий моменты в опорном сечении; k1 и k2 - коэффициенты, определяемые по табл. 24 и 25 в
зависимости от значений χ =
M0/Mк и λ = Qb/(2Mк) (Q - поперечная сила в опорном сечении). Таблица 24
Таблица 25
При этом интенсивность поперечного
армирования fх/u по грани шириной b должна быть не менее
интенсивности поперечного армирования по грани шириной h, подобранной в соответствия с п. 3.87. При значениях λ > 0,9 проверка прочности
из условий (168)
и (169)
может не производиться. 3.89. Проверку прочности по 1-й расчетной схеме, согласно п. 3.86, рекомендуется производить в
следующих случаях: а) если в пролетном
поперечном сечении с максимальным изгибающим моментом имеет место крутящий
момент; в этом случае рассчитывается пространственное сечение с серединой его
проекции в этом поперечном сечении, а также ряд других пространственных сечений
с большими крутящими моментами, если изгибающие моменты в середине этих сечений
близки к максимальному; б) если имеют место участки с
крутящими моментами, превышающими опорные крутящие моменты; в этом случае рассчитывается
пространственное
сечение с серединой его проекции в поперечном сечении с максимальным крутящим
моментом. В обоих случаях значение
β = c/b принимается равным β =
-χ + но не более 1/δ. При этом пространственное
сечение с длиной проекции c = βb не должно выходить за
пределы длины элемента. 3.90. Проверку прочности по 3-й расчетной схеме рекомендуется производить
следующим образом: а) Для неразрезных балок
рассматривается пространственное сечение с серединой его проекции в нулевой
точке эпюры M и проверяется армирование у
наименее армированной грани, нормальной плоскости изгиба. В этом случае прочность
проверяется из условий: если γ ≤ 0,5 Mк ≤ RаFа(h0 - a')2γ если γ > 0,5 Mк ≤ RаFа(h0 - a')2 где
Mк принимается по сечению в
нулевой точке эпюры M. Длина проекции
пространственного сечения, проверяемого из условий (171) или (172),
равна
где γ принимается не менее 0,5. Если расположение нулевой
точки эпюры M может изменяться при
различных комбинациях нагрузок, то в расчете из условий (171) и
(172)
учитывают такое расположение нулевой точки, при котором расстояние ее от опоры a равно или больше c/2, а усилие Mк имеет максимальное значение.
Если нулевая точка не может отстоять от
опоры дальше чем на расстоянии c/2, расчет по 3-й расчетной схеме следует вести общим методом, согласно
п. 3.86,
принимая β = 2a/b. б) Для шарнирно-опертых балок
рассматривается пространственное сечение, начинающееся у опоры. В этом случае прочность
проверяется из условия Mк
≤ Rа.хfх при λ
≥ 0,35
при λ
< 0,35
Усилия Q и Mк принимаются по опорному
сечению. Значения fх принимаются по сжатой от
изгиба грани. Элементы таврового,
двутаврового и других сечений, имеющих входящие углы
3.91. Поперечное сечение элемента следует разбивать на ряд прямоугольников
(см. рис. 49), при этом если высота свесов полок или ширина ребра переменны, следует
принимать средние высоту свесов или ширину ребра. Рис. 49. Разбивка на
прямоугольники сечений, имеющих входящие углы, при расчете на кручение с
изгибом Рис. 50. Схемы расположения
сжатой зоны в пространственном сечении железобетонного элемента двутаврового
сечения, работающего на кручение с изгибом а -
1-я схема; б - 3-я
схема; в - 2-я схема; с - центр тяжести продольной
растянутой арматуры Рис. 51. Схемы расположения
сжатой зоны в пространственном сечении железобетонного элемента таврового
сечения, работающего на кручение с изгибом а -
1-я схема; б - 3-я
схема; в - 2-я схема; с -
центр тяжести продольной растянутой арматуры Рис. 52. Схемы расположения
сжатой зоны в пространственном сечении железобетонного элемента Г-образного
сечения, работающего на кручение с изгибом а -
1-я схема; б - 3-я
схема; в и г - 2-я схема; с - центр тяжести продольной
растянутой арматуры Размеры поперечного сечения
должны удовлетворять условию Mк ≤ 0,1RпрΣbi2hi, (174) где hi, bi - соответственно больший и меньший размеры
каждого из составляющих сечение прямоугольников. Кроме того, должно
соблюдаться требование п. 3.30. Если в пределах высоты
сечения имеются полки (выступы), нижние и верхние грани которых не являются
продолжением соответствующих граней элемента, то расчет ведется без учета этих
полок как для элемента прямоугольного сечения согласно пп. 3.85 - 3.90. 3.92. Расчет тавровых, двутавровых, Г-образных и т.п. сечений проводится для
схем расположения сжатой зоны пространственного сечения, указанных на рис. 50 - 52. При этом проверяется
продольная и поперечная арматура, расположенная в растянутой зоне. Для любой из этих схем расчет
пространственного сечения производится из условия где Fа, h0, b, bр, x - значения, соответствующие
рассматриваемой расчетной схеме рис. 50 - 52 и определяемые как для плоского
сечения изгибаемого элемента; при расчете по 2-й схеме (рис. 50,в, 51,в, 52,в,
г) не учитываются сжатые свесы
полки, выступающие за грань полки меньшей ширины, либо за грань стенки (при
отсутствии другой сжатой полки); k, χ - см. п. 3.86; fх, u - площадь поперечных стержней, расположенных в одном
поперечном сечении в растянутой зоне (при данной расчетной схеме), и шаг этих
стержней; c -
длина проекции линии, ограничивающей сжатую зону пространственного сечения, на
продольную ось элемента, принимаемая равной для 1-й и 3-й схем (рис. 50,а, б, 51,а, б, 52,а,
б): c = 2h + b + 2bр - 2b0, (176) а для 2-й схемы (рис. 50,в, 51,в, 52,в,
г) с = 2h + 2bсв + b, (177) при этом длина c не должна выходить за пределы элемента, а также
участка его длины с однозначными эпюрами внешних усилий, учитываемыми в формуле
(175); h0х - расстояние от наиболее сжатой (при данной расчетной схеме) грани
до равнодействующей усилий в поперечных стержнях растянутой зоны. Расчет по 3-й расчетной схеме
не производится, если удовлетворяется условие M
> Mк Следует учитывать также
указание п. 3.85. Учитываемое в расчете
значение RаFа принимается не более величины
где значение γмин принимается равным при 1-й расчетной схеме -
при 2-й расчетной схеме -
γмин = 0,3; при 3-й расчетной схеме -
γмин = 0,2. При этом значения fх, Fа, b, bр должны соответствовать расчетным
схемам на рис. 50
- 52. Элементы кольцевого
сечения с продольной арматурой, равномерно распределенной по
окружности
3.93. Размеры поперечного
кольцевого сечения элемента должны удовлетворять условию Mк ≤ 0,08Rпрπ(r13 - r23), (179) где r1, r2 - соответственно наружный и внутренний радиусы
кольцевого сечения. Расчет пространственного
сечения (рис. 53)
производится из условия где β = c/b; b, c - длина проекции линии, ограничивающей сжатую зону,
соответственно на поперечное сечение элемента и на его продольную ось (рис. 53);
значение b принимается равным:
а значение c определяется согласно п. 3.94; χ -
принимается согласно п. 3.86 как для 1-го расчетного сечения; αк - относительная площадь
сжатой зоны бетона, определяемая по формуле (121) либо при αк
< 0,15 по формуле (124) п. 3.71; Fа.к - площадь сечения всей продольной арматуры; A и B - коэффициенты, определяемые
по формулам: при αк > 0,15 A = (1 - 1,7αк)( при αк ≤ 0,15 A = 0,75
Коэффициент B может определяться по графику рис. 54;
fх, u -
площадь сечения поперечного стержня и шаг этих стержней. Значение γ
принимается не менее γмин = 0,5/(1 + χ) и
не более γмакс = 1,5/(1 + χ). Рис. 53. Пространственное
сечение железобетонного элемента кольцевого поперечного сечения, работающего на
кручение с изгибом 1 - плоскость действия изгибающего момента Рис. 54. График коэффициента В для расчета на кручение с изгибом
элементов кольцевого поперечного сечения Если γ < γмин, в расчетных формулах
следует величину RаFа.к умножать на отношение γ/γмин. 3.94. Проверка условия (180) производится для пространственных сечений, в которых длина проекции c = βb не выходит за пределы участка,
на котором учитываемые в расчете усилия не меняют знаки и, кроме того, значение
c принимается не более cмакс = 2πr1(1 - αк). Для элементов с постоянным
сечением по длине рекомендуется проверять несколько пространственных сечений,
начинающихся от нормального сечения с наибольшим значением Mк, а при постоянных значениях Mк - от сечения с максимальными
значениями M. Для элементов с переменным
сечением по длине рекомендуется проверять несколько пространственных сечений,
расположенных в разных местах по длине и при значениях β, равных β = -χ + при этом длина проекции c = βb не должна выходить за
пределы длины элемента, а размеры поперечного сечения принимаются
соответствующими середине пространственного сечения. Примеры
расчета
Элементы, работающие на
кручение с изгибом Пример
43. Дано:
ригель перекрытия торцевой рамы многоэтажного промздания с поперечным сечением
приопорного участка по рис. 55,а, эпюры крутящих и изгибающих моментов
и эпюра поперечных сил по рис. 55,б; крутящие моменты получены при
действии вертикальных постоянных и длительных нагрузок; изгибающие моменты и поперечные силы
получены при действии вертикальных и ветровых нагрузок; бетон марки М 300;
продольная и поперечная арматура класса А-III (Rа = Rа.с
= 3400 кгс/см2, Rа.х = 2700 кгс/см2). Требуется подобрать шаг и
диаметр поперечных стержней и проверить прочность ригеля на совместное действие
кручения и изгиба. Рис. 55. К примеру расчета 43 Расчет. Поскольку сечение имеет
входящие углы, проверим условие (174) п. 3.91, разбив сечение на два
прямоугольника с размерами 80 × 32 и 15,5 × 25 см и приняв Rпр = 115 кгс/см2
(т.е. при mб1 = 0,85): 0,1RпрΣbi2hi = 0,1·115(322·80
+ 15,52·25) = 10,1 тс·м > Mк.макс = 8,56 тс·м, т.е. условие (174) удовлетворяется. Расчет прочности ведем как
для прямоугольного сечения с размерами b = 30 см и h =
80 см, так как нижняя грань ригеля и выступающая полка образуют угол. Так как 0,5Qb = 0,5·47,2·0,3 = 7,08 тс·м
< Mк = 8,56 тс·м, то
согласно п. 3.85
производим расчет пространственных сечений. Интенсивность вертикальных
хомутов fх/u определяем согласно п. 3.87. Предварительно определим
коэффициенты δ1, A, γ:
где Fа2 = 20,36 + 1,54 + 3,8 + 6,16
= 31,86 см2 (2Æ36 + Æ14 + Æ22 + Æ28). Так как усилия Mк и Q линейно уменьшаются от опоры
к пролету, значение γ определяем по формуле (166), предварительно вычислив
коэффициент k. Уменьшение усилий Mк и Q на единице длины элемента
равно (см. рис. 55,б): mк =
8,56/2,45=3,49 тс; p = 47,2/3 =
15,75 тс/м;
Тогда
Принимаем γ =
0,287. Проверяем условие (167):
т.е. условие (167) удовлетворяется. Необходимую интенсивность
хомутов определяем по формуле (163):
Принимая шаг вертикальных
хомутов u = 10 см, находим их диаметр dх. fх = 0,144·10 = 1,44 см2. Принимаем dх = 14 мм (fх =1,54 см2). Проверим достаточность продольной
и поперечной арматуры, установленной у верхней растянутой грани приопорного
участка ригеля, согласно указаниям п. 3.88 (1-я расчетная схема). Шаг
и диаметр хомутов, расположенных у этой грани, принимаем такими же, как для
вертикальных хомутов, т.е. u =
10 см, fх = 1,54 см2. Из рис. 55,а
находим Fа = 43,8 см2 (4Æ36 + 2Æ14) и F'а = 19,92 см2 (2Æ22 + 2Æ28); a' = 5 см. По формуле (156)
определяем высоту сжатой зоны x,
принимая Rпр = 145 кгс/см2
(т.е. при mб1 = 1,1, поскольку учитывается
ветровая нагрузка):
χ = M0/Mк = 50/8,56 = 5,8; λ = Qb/(2Mк) = 47,2·0,3/(2·8,56) = 0,827
< 0,9 и b/h = 30/80 = 0,375 находим k1 = 0,974 и k2 = 1,325. Проверяем условия (168) и
(169),
принимая h0 = 80 - 9 = 71 см: k1RаFа(h0 - 0,5x) =
0,974·3400·43,8(71 - 0,5·18,66) = 8940000 кгс·см = 89,4 тс·м > M0 = 50 тс·м; k2Rа.хfх т.е. прочность по 1-й расчетной схеме обеспечена. Проверим прочность
пространственного сечения по 3-й расчетной схеме, согласно п. 3.90
«а», принимая середину проекции пространственного сечения в нулевой точке эпюры
M. Поскольку менее армирована
нижняя грань ригеля, принимаем Fа = 19,92 см2 (2Æ22 + 2Æ28). Шаг и диаметр хомутов,
расположенных у нижней грани, принимаем такими же, как и для вертикальных хомутов,
т.е. u = 10 см и fх = 1,54 см2. Вычислим значения γ, δ и c:
Из рис. 55,б
видно, что левая нулевая точка эпюры M
отстоит от опоры дальше чем на c/2 =
106,7/2 = 53,3 см. При других комбинациях нагрузок нулевая точка может быть
существенно приближена к опоре и учитываемое в расчете значение Mк может возрасти, поэтому
принимаем невыгоднейшее расположение нулевой точки на расстоянии c/2 = 53,3 см от опоры. Значение Mк на этом расстоянии равно Mк = 8,56(2,45 - 0,533)/2,45 = 6,7 тс·м. Поскольку γ
< 0,5, проверяем условие (171). Из рис. 55
принимаем h0 = 80 - 5 = 75 см; a' = 9
см; RаFа(h0 - a')2γ т.е. прочность по 3-й расчетной схеме обеспечена. Пример
44. Дано:
балка перекрытия с поперечным сечением по рис. 56,а; эпюры крутящих и
изгибающих моментов и эпюра расчетных поперечных сил по рис. 56,б;
бетон марки М 300 (Rпр =
115 кгс/см2 при mб1 = 0,85); продольная и
поперечная арматура класса А-III (Rа = Rа.с = 3400 кгс/см2, Rа.х = 2700 кгс/см2).
Требуется проверить прочность балки на совместное действие кручения и изгиба. Рис. 56. К примеру расчета 44 Расчет. Разбиваем поперечное сечение
на два прямоугольника и проверяем условие (174): 0,1RпрΣbi2hi = 0,1·115(202·40
+ 352·40) = 7,48 тс·м > Mк = 4 тс·м. Проверяем требование п. 3.30: 0,35Rпрbh0 = 0,35·115·20·75 = 60400 кгс
> Q = 28 тс. Расчет проводим согласно п. 3.92 по
1-й схеме. Принимаем h = 80 см; h0 = h0х = 75 см; b0 = b = 20 см; bр = 35 см; Fа = 24,13 см2 (3Æ32); F'а = 3,08 см2 (2Æ14); fх = 1,54 см2 (Æ14); u = 10 см. Определяем длину проекции c по формуле (176): c = 2h + b+ 2bр - 2b0 = 2·80 + 20+ 2·35 - 2·20 = 210 см. Так как c = 210 см превышает длину с
однозначной эпюрой Mк, принимаем c = 154 см. Значения M и Mк в сечении на расстоянии c/2 от опоры равны M = 21,5 тс·м, Mк = 4 тс·м и, следовательно, χ = M/Mк = 21,5/4 = 5,375; k = 1. Определим значение γмин:
Так как
то продольное армирование учитываем полностью. Высоту сжатой зоны определяем
как для прямоугольного сечения:
при этом x =
31,1 см < ξR/h0 = 0,625·75 = 46,9 см. Проверяем прочность из
условия (175):
т.е. прочность при 1-й схеме обеспечена. Расчет по 3-й схеме. Принимаем h = 80 см; h0 = h0х = 75 см; b0 = bр = 20 см; b = 35 см; Fа = 3,08 см2; F'а = 24,13 см2; fх = 1,54 см; u = 10 см; с = 2h + b + 2bр - 2b0 = 2·80 + 35 + 2·20 - 2·20 = 195 см >154 см. Принимаем аналогично с
расчетом по 1-й схеме c =
154 см; Mк = 4 тс·м; M = 21,5 тс·м. Проверяем условие (178):
т.е. расчет по 3-й схеме не производится. Расчет по 2-й схеме. Принимаем h = 20 см; h0 = h0х = 20 - 5 = 15 см; b = 80 см; bсв = 15 см; Fа = F'а = 10,71 см2 (1Æ32 + 1Æ12 + 1Æ14); fх = 1,54 см2 (Æ14); u = 10 см; c = 2h + 2bсв + b = 2·20 + 2·15 + 80 = 150 см
< 154 см; Mк = 4 тс·м; Q = 28 тс; γмин = 0,3. Так как
то продольную арматуру учитываем в расчете полностью. Высоту сжатой зоны определим
без учета сжатой арматуры, поскольку значение a' = 5 см составляет
значительную долю от величины h0 = 15 см:
Проверяем прочность из
условия (175),
учитывая, что b = bр:
т.е. прочность по 2-й схеме обеспечена. Расчет
железобетонных элементов на местное действие нагрузок
Расчет на местное
сжатие
3.95(3.44). При расчете на местное сжатие (смятие) элементов без косвенного
армирования должно удовлетворяться условие N ≤ μсмRсмFсм, (182) где N - продольная сжимающая сила от местной
нагрузки; Fсм - площадь смятия; μсм - коэффициент, принимаемый равным: при равномерном распределении
местной нагрузки на площади смятия - 1; при неравномерном
распределении местной нагрузки на площади смятия (под концами балок, прогонов,
перемычек) - 0,75; Rсм - расчетное сопротивление
бетона смятию, определяемое по формуле Rсм = γбRпр; (183) здесь при схеме приложения нагрузки
по рис. 57,а, в, г, е, и -
2,5; при схеме приложения нагрузки
по рис. 57,б,
д, ж - 1; Rпр - принимается как для бетонных конструкций (см. поз. 2 табл. 7); Fр - расчетная площадь, определяемая по указаниям п. 3.96. Если условие (182) не
удовлетворяется, то рекомендуется применять косвенное армирование в виде
сварных сеток и рассчитывать элемент в соответствии с п. 3.97. Рис. 57. Определение
расчетной площади Fр при расчете на местное сжатие 1 - расчетная площадь, учитываемая только при наличии косвенной арматуры 3.96(3.45). В расчетную площадь Fр включается
участок, симметричный по отношению к площади смятия (рис. 57). При этом должны
выполняться следующие правила: а) при местной нагрузке по
всей ширине элемента t в расчетную площадь включается участок длиной не более t в каждую сторону от границы местной нагрузки (рис. 57,а); б) при местной краевой
нагрузке по всей ширине элемента расчетная площадь Fр равна площади смятия Fсм (рис. 57,б); в) при местной нагрузке в
местах опирания концов прогонов и балок в расчетную площадь включается участок
шириной, равной глубине заделки прогона или балки, и длиной не более расстояния
между серединами примыкающих к балке пролетов (рис. 57,в); если расстояние
между балками превышает двойную ширину элемента, длина расчетной площади
определяется как сумма ширины балки и удвоенной ширины элемента (рис. 57,г); г) при местной краевой
нагрузке на угол элемента (рис. 57,д)
расчетная площадь Fр равна площади смятия Fсм; д) при местной нагрузке,
приложенной на части длины и ширины элемента, расчетная площадь принимается
согласно рис. 57,е. При наличии нескольких нагрузок
указанного типа расчетные площади ограничиваются линиями, проходящими через
середину расстояний между точками приложения двух соседних нагрузок; е) при местной краевой нагрузке,
расположенной в пределах выступа стены (пилястры) или простенка таврового
сечения, расчетная площадь равна площади смятия Fсм (рис. 57,ж); ж) при определении расчетной
площади для сечений сложной формы не должны учитываться участки, связь которых
с загруженным участком не обеспечена с необходимой надежностью (например,
участки 2 и 3 на рис. 57,и). Примечание.
При местной нагрузке от балок, прогонов, перемычек и других элементов,
работающих на изгиб, учитываемая в расчете глубина опоры при определении Fсм и
Fр принимается не более 20 см. 3.97(3.46). При расчете на местное сжатие железобетонных элементов с косвенным
армированием в виде сварных поперечных сеток должно удовлетворяться условие N ≤ R*смFсм, (184) где Fсм - площадь смятия; R*см -
приведенная прочность бетона на смятие, определяемая по формуле R*см = Rпрγб + kμксRасγк. (185) В формуле (185):
но не более 3,5; γк = 4,5 - 3,5Fсм/Fя; (187) Fр -
расчетная площадь, определяемая в соответствии с требованиями п. 3.96
(для схем приложения местной нагрузки по рис. 57,б, д, ж в нее включается площадь, ограниченная
пунктирной линией); Fя -
площадь бетона, заключенного внутри контура сеток косвенного армирования; для
схем приложения местной нагрузки по рис. 57,а, в, г, е, и должно
удовлетворяться условие Fсм < Fя ≤ Fр, а для схем по рис. 57,б, д, ж Fя должно быть не менее Fр, при этом в формулу (187)
подставляется Fя = Fр; Rаc, k, μкc - обозначения те же, что и в п. 3.60. Рис. 58. Схема пирамиды
продавливания при угле наклона ее боковых граней к горизонтали а -
равном 45°; б - большем
45° Рис. 59. Схема пирамиды
продавливания во внецентренно-нагруженном фундаменте Расчет на продавливание
3.98(3.47). Расчет на продавливание
плитных конструкций (без поперечной арматуры) от действия сил, равномерно
распределенных на ограниченной площади, должен производиться из условия P ≤ Rрbсрh0, (188) где P - продавливающая сила; bср - среднее арифметическое величин периметров верхнего и нижнего
основания пирамиды, образующейся при продавливании в пределах рабочей высоты
сечения h0. При определении величин bср и P предполагается, что продавливание происходит по
боковой поверхности пирамиды, меньшим основанием которой служит площадь
действия продавливающей силы, а боковые грани наклонены под углом 45° к
горизонтали (рис. 58). Величина продавливающей силы P принимается равной величине продольной силы N, действующей на пирамиду продавливания, за вычетом нагрузок, приложенных
к большему основанию пирамиды продавливания (считая до плоскости расположения
растянутой арматуры) и сопротивляющихся продавливанию. Если схема опирания такова,
что продавливание может происходить только по поверхности пирамиды с углом
наклона боковых граней больше 45° (например, в свайных ростверках, рис. 58,б),
правая часть условия (188) умножается на величину h0/c, но не более 2,5, где c - длина горизонтальной
проекции боковой грани пирамиды продавливания. При установке в пределах
пирамиды продавливания поперечной арматуры расчет должен производиться из
условий: P
≤ 1,4Rрbсрh0; (189) P ≤ Rа.хFх.п, (190) где Fх.п - площадь
поперечной арматуры, пересекающей боковые грани пирамиды продавливания. Поперечное армирование и
размеры плит независимо от результатов расчета должны удовлетворять
конструктивным требованиям пп. 5.4 и 5.79. Кроме расчета на
продавливание должен производиться расчет на действие поперечных сил. В случае продавливания
безбалочных перекрытий при наличии стальных воротников должны учитываться
специальные указания. 3.99. Для центрально-нагруженных
прямоугольных, а также внецентренно-нагруженных квадратных и прямоугольных
фундаментов расчет на продавливание производится из условия (188)
отдельно для каждой грани пирамиды продавливания. При этом средний периметр
пирамиды продавливания bср заменяется средним размером ее грани bср =
(b0 +
bн)/2
(см. рис. 59), а
величина силы P принимается равной Fpгр, где F - часть площади основания
фундамента, ограниченная нижним основанием рассматриваемой грани пирамиды
продавливания и продолжением соответствующих ребер (многоугольник AВСДЕG, см. рис. 59); pгр - наибольшее краевое
давление на грунт при расчете в плоскости эксцентрицитета, а при расчете в
перпендикулярной плоскости pгр - среднее давление на грунт в
пределах расчетной площади F (многоугольника BCFH). Значение pгр определяется без учета веса
фундамента и грунта на его уступах. Для ступенчатых фундаментов
должна производиться проверка на продавливание от каждой вышележащей ступени
(рис. 63). Если рабочая высота
фундамента (или его ступени) превышает 0,6 вылета соответствующей консоли lк (см. рис. 59),
следует также провести расчет этой консоли на действие поперечной силы из
условия (64)
п. 3.42. При соединении колонны с
фундаментом стаканного типа расчет фундамента на продавливание производится с
учетом указаний специального руководства. Расчет на отрыв
3.100(3.48). Расчет на отрыв растянутой зоны элемента от действия нагрузки,
подвешенной к элементу или приложенной в пределах высоты его сечения (рис. 60), должен производиться из
условия Pот ≤ RаFх.д, (191) где Pот - отрывающее усилие; Fх.д -
площадь дополнительной, сверх требуемой по расчету наклонного сечения,
поперечной арматуры (подвески, хомуты и т.п.), расположенной на длине зоны
отрыва s. Длина зоны отрыва s при нагрузке, распределенной
по ширине b1, принимается
равной s = 2h1 + b1, (192) где h1 - расстояние
от уровня передачи нагрузки (при примыкающих друг к другу элементах - от центра
тяжести сжатой зоны элемента, вызывающего отрыв) до центра тяжести сечения
арматуры A. Если при отсутствии кручения
поперечная арматура в виде хомутов поставлена сверх требуемой по расчету
наклонного сечения, то площадь дополнительных хомутов на длине зоны отрыва s принимается равной
где ΣFх - площадь всех хомутов на длине зоны отрыва s; Q1 и Q2 - поперечные силы в месте приложения силы Pот (т.е. Q1 - Q2 = Pот). 3.101. Входящие углы в растянутой
зоне элементов, армируемые пересекающимися продольными стержнями (рис. 61),
должны иметь поперечную арматуру, достаточную для восприятия: а) равнодействующей усилий в
продольных растянутых стержнях, не заведенных в сжатую зону, равной P1 = 2RаFа1cos(γ/2); (194) б) 35 % равнодействующей
усилий во всех продольных растянутых стержнях P2 = 0,7RаFаcos(γ/2) (195) Рис. 60. Схема определения
длины зоны отрыва 1 - центр тяжести сжатой зоны сечения примыкающего элемента Рис. 61. Армирование
входящего, угла расположенного в растянутой зоне железобетонного элемента Необходимая по расчету из
этих условий поперечная арматура должна быть расположена на длине s = htg(4γ/8). (196) Сумма проекций усилий в
поперечных стержнях (хомутах), располагаемых по этой длине, на биссектрису угла
γ должна составлять не менее
суммы P1 +
P2, т.е. ΣRаFхcosα > P1 + P2. (197) В формулах (194) -
(197)
приняты обозначения: Fа - площадь сечения всех
продольных растянутых стержней; Fа1 -
площадь сечения продольных растянутых стержней, не заанкеренных в сжатой зоне; γ -
входящий угол в растянутой зоне элемента; ΣFх - площадь сечения поперечной арматуры в пределах
длины s; α - угол наклона поперечных
стержней к биссектрисе угла γ. Примеры расчета
Расчет на местное сжатие
(смятие) Пример
45. Дано: на
железобетонный фундамент опирается стальная стойка, центрально-нагруженная
усилием N = 100 тс, как показано на
рис. 62; бетон фундамента марки М 150 (Rпр = 60 кгс/см2 при mб1 = 0,85). Требуется проверить прочность
бетона под стойкой на местное сжатие (смятие). Расчет. Расчет производим в
соответствии с указаниями пп. 3.95 и 3.96. Расчетную площадь Fр определяем по п. 3.96,д. Рис. 62. К примеру расчета 45 Согласие рис. 62,
имеем c1 = 20 см; c2 = 20 см < b = 80 см; A = 20·2 + 30 = 70 см; B = 20·2 + 20 = 60 см; Fр = A·B = 70·60 = 4200 см2. Площадь смятия равна Fсм = 30·20 = 600 см2. Коэффициент γб равен
Определяем расчетное
сопротивление бетона смятию по формуле (183), принимая Rпр по табл. 7 как для
бетонной конструкции - Rпр
= 50 кгс/см2; Rсм
= γбRпр =
1,9·50 = 95 кгс/см2. Проверяем условие (182),
принимая μсм = 1 как при равномерном распределении нагрузки.
Тогда μсмRсмFсм = 95·600 = 57000 кгс = 57 тс
< N = 100 тс, т.е. прочность бетона на местное сжатие не обеспечена
и необходимо применить косвенное армирование. Принимаем косвенное
армирование в виде сеток из обыкновенной арматурой проволоки класса В-I диаметром 3 мм, с ячейкой 100 × 100 мм и шагом
по высоте s = 100 мм (Rас = 3150 кгс/см2). Проверяем прочность согласно
указаниям п. 3.97. Так как γб =
1,9 < 3,5, то в расчет вводим γб = 1,9. Коэффициент косвенного
армирования сетками μкс определяем по формуле (88). Из рис. 62
имеем: n1 = 5; l1 = 30 см; n2 = 4; l2 = 40 см; fс1 = fс2 = 0,071 (Æ3); Fя= l1·l2 = 30·40 = 1200 см2
> Fсм = 600 см2. Тогда
По формулам (87) и (86)
определяем αс и k:
Коэффициент γк равен γк = 4,5 - 3,5Fсм/Fя = 4,5 - 3,5·600/1200 = 2,75. Приведенная прочность бетона R*см определяется
по формуле (185): R*см = Rпрγб
+ kμксRасγк = 60·1,9 +
3,56·0,00183·3150·2,75 = 1,70,4 кгс/см2. Проверяем условие (184): R*смFсм = 170,4·600 = 102,2 тс > N = 100 тс, т.е. прочность бетона обеспечена. Расчет на продавливание Пример
46. Дано:
внецентренно-нагруженный прямоугольный фундамент с размерами по рис. 63;
бетон марки М 150 (Rр = 5,4 кгс/см2 при
учете mб1 = 0,85); нормальная сила,
приложенная к верхнему обрезу фундамента N
= 220 тс; момент относительно оси проходящей через центр тяжести подошвы
фундамента параллельно меньшей его стороне, M = 11 тс·м. Рис. 63. К примеру расчета 46 Требуется проверить прочность
фундамента на продавливание. Расчет. Проверяем грань пирамиды
продавливания, параллельную меньшей стороне подошвы фундамента и начинающуюся
от грани подколонника (рис. 63). Площадь подошвы фундамента и
ее момент сопротивления равны: Fф = 1,8·3 = 5,4 м2;
Wф = 1,8·32/6 = 2,7
м3. Определяем наибольшее краевое
давление на грунт по формуле Pгр = N/Fф + M/Wф = 220/5,4 + 11/2,7 = 4,48 кгс/см2. Рабочая высота фундамента h0 = 60 - 5 = 55 см. Верхняя сторона грани
пирамиды продавливания равна размеру подколонника, т.е. b0 = 90 см. Нижняя сторона грани пирамиды
продавливания на уровне рабочей арматуры равна всей ширине подошвы, т.е. bн = 180 см, поскольку: b0 + 2h0 = 90 + 2·55 = 200 см > bн = 180 см; bср = (b0 + bн)/2 = (90 + 180)/2 = 135 см. Определяем площадь F прямоугольника AВСД
(рис. 63),
с которой собирается нагрузка, действующая на рассматриваемую грань: F = 180·50 = 9000 см2. Проверяем условие (188): Rрbсрh0 = 5,4·135·55 = 40,1 тс @ P = pгрF = 4,48·9000 = 40,3 тс, т.е. прочность рассматриваемой грани обеспечена. Поскольку рабочая высота h0 = 55 см < 0,6lк = 0,6·105 = 63 см (см. рис. 63),
расчет на действие поперечной силы не производим. Проверяем грань пирамиды
продавливания, начинающуюся от грани верхнего уступа. Рабочая высота нижнего
уступа равна h0 = 30 - 5 = 25 см. Верхняя и нижняя стороны
грани пирамиды продавливания равны ширине подошвы фундамента, т.е. bср = 180 см. Определяем площадь F прямоугольника ABEG (рис. 63), с
которой собирается нагрузка, действующая на рассматриваемую грань: F = (45 - 25)180 = 3600 см2. Проверяем условие (188): Rрbсрh0 = 5,4·1800·25 = 24300 кгс
> Fpгр = 3600·4,48 = 16100 кгс, т.е. прочность рассматриваемой грани обеспечена. Поскольку рабочая высота
нижнего уступа h0 = 25 см < 0,6lк1 = 0,6·45 = 27 см (см. рис. 63),
расчет нижнего уступа на действие поперечной силы не производим. Из рис. 63
видно, что грань пирамиды продавливания, параллельная большей стороне
фундамента, не пересекает подошву фундамента, поэтому прочность на
продавливание по этой грани заведомо обеспечена. Расчет
коротких консолей
3.102(3.37). Короткие консоли (lк ≤ 0,9 h0, рис. 64),
поддерживающие балки, фермы и т.п., следует рассчитывать на действие поперечной
силы из условия в котором правая часть неравенства принимается не
более 2,5Rрbh0. Рис. 64. Расчетная схема для
короткой консоли при расчете ее по прочности на действие поперечной силы В условии (198): Qк - поперечная
сила, действующая на консоль в пределах ее вылета; k4 - коэффициент, принимаемый равным: при кранах весьма тяжелого
режима работы - 0,5, при кранах тяжелого режима работы - 0,75, при кранах
среднего и легкого режима работы - 1, при статической нагрузке - 1; a - расстояние от точки приложения силы Qк до опорного сечения консоли
(рис. 64); b и h0 - принимаются в
опорном сечении. Для коротких консолей,
входящих в жесткий узел рамной конструкции, в правую часть условия (198)
вводится коэффициент, равный 1,25. Расчет согласно указаниям
настоящего пункта распространяется на короткие консоли с углом наклона α
сжатой грани консоли к горизонтали не более 45 °С и с высотой сечения hк у свободного края не менее 1/3
высоты опорного сечения h (рис. 64). Напряжение смятия в местах
передачи нагрузки на консоль не должно превышать Rпр. При определении значения a для консолей, на которые шарнирно опираются сборные
балки, идущие вдоль вылета, при отсутствии специальных выступающих закладных
деталей, фиксирующих площадку опирания, принимается, что балка опирается на
площадку длиной lоп =
Qк/(bбRпр) (где bб - ширина площадки опирания
балки на консоль), расположенную у свободного конца консоли (рис. 65). При
этом нагрузка на консоль принимается распределенной равномерно на длине
площадки опирания. Нагрузка на короткую консоль, входящую в жесткий узел рамной
конструкции, принимается равномерно распределенной по фактической площадке
опирания ригеля. Рис. 65. Расчетная схема для
короткой консоли при отсутствии фиксированной площадки опирания а - при lоп < lк; б - lоп < lк Во всех случаях, если вылет
консоли lк меньше длины площадки
опирания (рис. 65,б),
в условии (198)
учитывается нагрузка на консоль, находящаяся только в пределах вылета консоли. 3.103. В коротких консолях,
примыкающих к колоннам или к другим элементам большей высоты, выступающим за
сжатую грань консолей не менее чем на половину высоты консоли в месте
примыкания ее к колонне или к другому элементу, сечение продольной арматуры
подбирается по изгибающему моменту, действующему по грани примыкания консоли к
элементу, увеличенному на 25 %. В остальных случаях, а также если консоль
является продолжением свободно лежащей на опоре балки или плиты, сечение
продольной арматуры подбирается по моменту, действующему по оси опоры и
увеличенному на 25 %. При опирании сборных балок,
идущих вдоль вылета консоли, при отсутствии специальных выступающих закладных
деталей, фиксирующих площадку опирания, изгибающий момент определяется по
формуле При этом если lк > lоп = Продольная арматура
соответствующего сечения должна быть доведена до конца консоли. В консолях, для которых коэффициент
k4 в условии (198)
составляет более 0,5 и расстояние l3 от центра груза до конца
арматуры (см. рис. 64) не превышает: при бетоне проектной марки ниже
М 300 - 15d: при бетоне проектной марки М
300 и выше - 10d, продольная арматура должна
быть снабжена анкерами в виде шайб или уголков. Конструкция анкеров должна
удовлетворять требованиям п. 5.49 «б». Кроме того, армирование
консолей должно удовлетворять требованиям п. 5.81. Примечание. Постановка анкеров не обязательна в консолях, на которые опираются
сборные балки, идущие вдоль вылета консолей, если стыки этих балок надежно
замоноличены, арматура в них поставлена как в раме с жесткими узлами, а нижняя
арматура балок приварена к арматуре консолей через закладные детали. Примеры расчета
Короткие консоли Пример
47. Дано: на
короткую консоль колонны опирается свободно лежащая сборная балка (рис. 66) с
шириной понизу bб = 130 см, идущая вдоль
вылета консоли; ширина консоли (колонны) b = 40 см; вылет консоли lк = 35 см; угол наклона сжатой
грани консоли к горизонтали α = 45°; марка бетона колонны М 200 (Rпр = 75 кгс/см2, Rр = 6,5 кгс/см2
при mб1 = 0,85); продольная и
наклонная арматура консоли класса А-III (Rа = 3400 кгс/см2);
нагрузка на консоль от балки равна Qк = 50 тс. Рис. 66. К примеру расчета 47 Требуется определить
минимальные размеры консоли и площадь сечения продольной и наклонной арматуры
консоли. Расчет. Определяем расчетную длину
площадки опирания балки на консоль.
Расчетная длина площадки опирания
меньше вылета консоли lоп = 22,22 см < lк = 35 см и не превышает
фактической длины площадки опирания (35 - 5) см (т.е. напряжения смятия не
превышают Rпр). Минимальную рабочую высоту
консоли определяем из условия (198) в опорном сечении a = lк - lоп/2 = 35 - 22,2/2 = 23,9 см; k4 = 1 (как для статической
нагрузки);
Принимаем h0 = 77 см, а h = 80 см. Тогда высота
свободного края консоли равна hк = h - lкtgα =
80 - 35tg45° = 45 см > h/3 = 80/3 = 26,7 см. Оставляем hк = 45 см. Определяем момент в сечении
примыкания консоли к колонне по формуле (199):
Принимая в расчете большое
количество сжатой арматуры, площадь растянутой арматуры определяем из формулы (19):
Принимаем 3Æ16 (Fа = 6,03 см2). Так как h = 80 см > 2,5a = 2,5·23,9 = 59,8 см, согласно п. 5.81, консоль армируется
отогнутыми стержнями и наклонными хомутами, суммарную площадь которых
определяем по формуле fо = 0,002bh0 = 0,002·40·77 = 6,16 см2. Принимаем fо = 6,16 см2 (4Æ14). Расчет закладных деталей и соединений элементов
Расчет закладных деталей
3.104(3.49). Расчет анкеров, приваренных втавр к плоским элементам стальных
закладных деталей, на действие изгибающих моментов, нормальных и сдвигающих сил
(рис. 67) должен производиться по формуле где Fан - суммарная площадь поперечного сечения анкеров
наиболее напряженного ряда; Nан - наибольшее растягивающее усилие в одном ряду анкеров, равное Qан - сдвигающее усилие, приходящееся на один ряд анкеров, равное здесь N'ан - наибольшее
сжимающее усилие в одном ряду анкеров, определяемое по формуле M, N и Q - соответственно момент, нормальная и
сдвигающая силы, действующие на закладную деталь; величина момента определяется
относительно оси, расположенной в плоскости наружной грани пластины и
проходящей через центр тяжести всех анкеров; nан - число рядов анкеров (при определении сдвигающего усилия Qан учитывается не более четырех
рядов); z - расстояние между крайними
рядами анкеров; k1 - коэффициент, определяемый по формуле но принимаемый не менее 0,15; коэффициент ω
принимается равным: ω = 0,3Nан/Qан при N'ан ≥ 0; ω = 0,6N/Q при N'ан < 0; k - коэффициент, определяемый для анкерных стержней
диаметром 8 - 25 мм и тяжелого бетона марок М 150 - М 600 по формуле но принимаемый не более 0,7; для бетона марки
выше М 600 коэффициент k принимается как для марки М
600. Рис. 67. Схема усилий, действующих
на закладную деталь В формуле (205): Rпр, Rа - в кгс/см2; fан - площадь анкерного стержня наиболее напряженного ряда, см2. Коэффициент k можно также определять по табл. 26. Площадь сечения анкеров
остальных рядов должна приниматься равной площади сечения анкеров наиболее
напряженного ряда. В формулах (201) и
(203)
нормальная сила N считается
положительной, если она направлена от закладной детали, и отрицательной, если
она направлена к ней. Если нормальные усилия Nан и N'ан, а также сдвигающее усилие Qан при вычислении по формулам (201) -
(203)
получают отрицательные значения, то в формулах (200), (202) и (204)
они принимаются равными нулю. Кроме того, если Nан получает отрицательное
значение, то в формуле (202) принимается N'ан =
N. При расположении закладной
детали на верхней (при бетонировании) поверхности изделия коэффициент k уменьшается на 20 %, а значение N'ан принимается равным нулю. 3.105(3.50). Расчет анкеров, приваренных к пластине внахлестку, на действие
сдвигающей силы должен производиться по формуле Fан = Q/Rа, (206) Сопротивление анкеров,
приваренных внахлестку, действию сдвигающей силы учитывается при Q > N (где N - растягивающая сила) и угле отгиба
этих анкеров от 15 до 30°. При этом должны устанавливаться анкеры, приваренные
втавр и рассчитываемые по формуле (200) при k1 =
1 и при значении
Qан равном 0,1 от сдвигающего
усилия, определенного по формуле (202). Приваренные к пластине упоры
из полосовой стали или арматурных коротышей (см. п. 5.113) могут воспринимать не
более 30 % сдвигающей силы при напряжениях в бетоне под упорами, равных Rпр. При этом значение Q в формулах (202) и (206)
соответственно снижается. Таблица 26
3.106(3.51). Конструкция закладных деталей с приваренными к ним элементами,
передающими нагрузку на закладные детали, должна обладать достаточной
жесткостью для обеспечения равномерного распределения усилий между растянутыми
анкерами и равномерной передачи сжимающих усилий на бетон. Стальные элементы
закладных деталей и их сварные соединения рассчитываются согласно главе СНиП по
проектированию стальных конструкций. Толщина пластин закладных
деталей δп при анкерах, приваренных втавр, должна удовлетворять
условию где d - диаметр анкеров; Rср - расчетное сопротивление стали на срез, принимаемое согласно главе
СНиП по проектированию стальных конструкций (для стали класса С38/23 Rср = 1300 кгс/см2). 3.107. Если выполняется условие N'ан ≤ 0, (208) где N'ан - см. п. 3.104,
т.е. если все анкеры закладной детали растянуты, следует производить расчет на
выкалывание бетона следующим образом: а) при анкерах с усилением на
концах (см. п. 5.116) расчет производится из условия где П - площадь проекции на плоскость,
нормальную к анкерам, поверхности выкалывания, идущей от краев анкерных пластин
или высаженных головок всех анкеров под углом 45° к осям анкеров; при
эксцентрицитете силы N относительно
центра тяжести анкеров e0 = M/N размер площади П в направлении этого эксцентрицитета
уменьшается на 2e0 при соответствующем смещении
наклонной грани поверхности выкалывания (рис. 68); площади анкерных пластин
или высаженных головок, расположенных на поверхности выкалывания, не
учитываются; a1 и a2 -
размеры площади П; e1 и e2 -
эксцентрицитеты силы N относительно
центра тяжести площади П в
направлении соответственно размеров a1 и a2; б) при анкерах без усиления
на концах расчет производится из условия где Пh - то же, что и П при
поверхности выкалывания, идущей от анкеров на расстоянии h по длине анкера от пластины
закладной детали (рис. 69); ah1 и ah2 -
размеры площади Пh; eh1 и eh2 - эксцентрицитеты силы N относительно центра тяжести площади Пh в направлении соответственно размеров ah1 и ah2; Σfаi - площадь сечения всех анкеров, пересекающих поверхность
выкалывания; lхi - расстояние от конца i-го анкера до поверхности
выкалывания; lан - длина зоны анкеровки (см. п. 5.115); условие (210) проверяется при различных
значениях h, меньших длины анкеров. Если число рядов анкеров в
направлении эксцентрицитета e0 превышает два, то в условиях
(209)
и (210)
силу N можно уменьшить
на (1 - 2/nан)M/z (где nан, M и z - см. п. 3.104). Если N'ан ≥ 0, расчет на
выкалывание производится при длине анкеров, меньшей lан, и при наличии усиления на их концах из условия Nан ≤ 0,5П1Rр, (211) где Nан - см. п. 3.104; П1 - то же, что и П
при поверхности выкалывания, начинающейся от краев анкерных пластин или
высаженных головок анкеров наиболее растянутого ряда (рис. 70). Рис. 68. Схема выкалывания
бетона анкерами закладной детали с усилениями на концах при N'ан < 0 1 - точка приложения нормальной силы N; 2 - поверхность выкалывания; 3 - проекция
поверхности выкалывания на плоскость, нормальную к анкерам Рис. 69. Схема выкалывания
бетона анкерами закладной детали без усилений на концах при N'ан < 0 1 - точка приложения нормальной силы N; 2 - поверхность выкалывания; 3 - проекция
поверхности выкалывания на плоскость, нормальную к анкерам При этом для колонн расчет на
выкалывание можно не производить, если концы анкеров заведены за продольную
арматуру, расположенную у противоположной от закладной детали грани колонны, а
усиления анкеров в виде пластин или поперечных коротышей зацепляются за стержни
этой арматуры диаметром: не менее 20 мм при симметричном зацеплении и не менее
25 мм при несимметричном зацеплении (рис. 71). В этом случае участок
колонны между крайними рядами анкеров проверяется, согласно п. 3.32, на
действие поперечной силы, равной Q = Nан ± Qк, где Qк - поперечная сила на участке
колонны, прилежащем к наиболее растянутому ряду анкеров закладной детали;
значение Qк определяется с учетом
действующих на закладную деталь усилий. 3.108. Если сдвигающая сила Q действует на закладную деталь
в направлении к краю элемента (рис. 72), то при отсутствии анкеров,
приваренных внахлестку, следует производить расчет на откалывание бетона из
условия Q ≤ 0,5Rрbh1, (212) где h1 -
расстояние от центра тяжести анкеров закладной детали до края элемента в
направлении сдвигающей силы Q; b - ширина откалывающейся части
элемента, принимаемая не более 2h1. Если условие (212) не
выполняется, то к закладной детали приваривают внахлестку анкеры или по грани
элемента с закладной деталью устанавливают, согласно п. 3.100,
дополнительные хомуты, воспринимающие сдвигающую силу Q. 3.109. При наличии на концах анкеров закладной детали усилений в виде анкерных
пластинок или высаженных головок бетон под этими усилениями должен быть
проверен на смятие из условия Nсм ≤ γбRпрFсм, (213) где γб - коэффициент, определяемый
согласно п. 3.95
и принимаемый не более: 2,5 - при бетоне марок М 400 и ниже, 2 - при бетоне
марок выше М 400; Рис. 70. Схема выкалывания
бетона растянутыми анкерами закладной детали при N'ан ≥ 0 1 -
проекция поверхности выкалывания на плоскость, нормальную к анкерам; 2
- анкерная пластина Рис. 71. Конструкция
закладной детали, при которой не требуется расчет на выкалывание 1 - поперечные коротыши, приваренные контактной
сваркой к анкерам (2); 3 - анкерные пластинки; а - закладная деталь с коротышами,
симметрично зацепленными за продольную арматуру колонны; б - эпюра Q участка колонны с закладной деталью; в - анкеры закладной детали с анкерными пластинами, несимметрично
зацепленными за продольную арматуру колонны Рис. 72. Схема, принимаемая
при расчете на откалывание бетона анкерами закладной детали Fсм - площадь анкерной пластины или сечения высаженной головки за
вычетом площади сечения анкера; Nсм - сила смятия, определяемая следующим образом: а) для анкеров, приваренных
втавр, длиной lа не менее 15d, если вдоль анкера возможно образование трещин от растяжения бетона, Nсм = Nан/nа, (214) если образование таких трещин невозможно, б) для анкеров, приваренных
втавр, длиной lа менее 15d значение Nсм, определенное по формулам (214) и
(215),
увеличивается на
в) для анкеров, приваренных
внахлестку Nсм = Q/nот. В формулах настоящего пункта: Nан, nан и Qан - см. п. 3.104; nа - число анкеров наиболее напряженного ряда; lан - длина зоны анкеровки, определяемая согласно п. 5.48; nот - число анкеров, приваренных внахлестку. Примеры расчета
Расчет закладных
деталей Пример
48. Дано: к
закладной детали колонны приварен столик для опирания обвязочных балок; размеры
закладной детали, а также расположение и величины нагрузок от обвязочных балок
- по рис. 73;
анкеры из арматуры класса А-III (Rа = 3400 кгс/см2); бетон колонны марки М
200 (Rпр = 75 кгс/см2,
Rр = 6,5 кгс/см2 при
mб1 = 0,85). Требуется запроектировать
анкеры закладной детали и определить толщину пластины. Расчет. Принимаем расположение
анкеров, приваренных втавр, как показано на рис. 73. Суммарную площадь
поперечного сечения анкеров наиболее напряженного верхнего ряда определяем по
формуле (200). Для этого вычисляем момент
внешних сил M =
Ql = 15·0,15 = 2,25 тс·м (см. рис. 73). Принимая z = 30 см N = 0, определим наибольшее
растягивающее усилие в рассматриваемых анкерах по формуле (201): Nан = M/z = 2,25/0,3 = 7,5 тс. Сдвигающая сила Q = 15 тс, число рядов анкеров
nан = 3. Рис. 73. К примеру расчета 48 Сдвигающее усилие Qан, приходящееся на один ряд
анкеров, вычисляем по формуле (202), принимая Nан =
N'ан = 7,5 тс: Qан = (Q - 0,3N'ан)/nан = (15 - 0,3·7,5)/3 = 4,25 тс. Коэффициент k1 определяем по формуле (204). Так как N'ан > 0, ω = 0,3Nан/Qан = 0,3·7,5/4,25 = 0,529. Отсюда
Задаваясь диаметром анкеров
16 мм, по табл. 26 при марке бетона М 200 и анкерах из арматуры
класса А-III находим k = 0,41. Тогда
Принимаем по два анкера в
каждом ряду диаметром 18 мм (Fан = 5,09 см2). Проверим значение Fан при коэффициенте k, соответствующем принятому диаметру 18 мм, т.е. при k = 0,39:
Из условий размещения анкеров
в колонне длину анкеров принимаем равной 30 см, что меньше минимально
допустимой длины анкеров, равной lан = 35d = 35·1,8 = 63 см (см. табл. 48). Следовательно, согласно п.
5.116,
концы анкеров усиливаем высаженными головками диаметром dгол = 3d и проверяем
бетон на смятие под высаженной головкой и на выкалывание. При этом длина анкера
30 см >10d = 10·1,8 = 18 см, т.е.
допустима для анкеров с усилением на конце. Расчет на смятие ведем
согласно п. 3.109. Площадь смятия Fсм под высаженной головкой
одного анкера равна
Поскольку lа = 30 см > 15d = 15·1,8 = 27 см, а в
колонне со стороны закладной детали возможны растягивающие напряжения, значение
Nсм принимаем по формуле (214) Nсм = Nан/nа = 7,5/2 = 3,75 тс. Проверяем условие (213),
принимая γб = 2,5: γбRпрFсм = 2,5·75·20,3 = 3800 кгс =
3,8 тс > Nсм = 3,75 тс, т.е. прочность на смятие обеспечена. Расчет на выкалывание ведем
согласно п. 3.107. Поскольку N'ан > 0 и концы анкеров с усилением не заведены за
продольную арматуру колонны, расположенную у противоположной от закладной
детали грани, расчет ведем из условия (211). Вычисляем значение П1, принимая расположение анкеров по рис. 73. П1 = (5,4 + 2·30)40 -
2·3,14·5,42/4 = 2570 см2; 0,5П1Rр = 0,5·2570·6,5 = 8350 кгс = 8,35 тс > Nан = 7,5 тс, т.е. прочность на выкалывание обеспечена. Принятые расстояния между
анкерами в направлении поперек и вдоль сдвигающей силы, соответственно равные
28 см >4d = 4·1,8 = 7,2 см и 15 см
> 6d = 6·1,8 = 10,8 см,
удовлетворяют требованиям п. 5.114. Расстояние от оси анкера до грани
колонны, равное 6 см > 3d =
3·1,8 = 5,4 см, также удовлетворяет требованию п. 5.114. Определяем необходимую
толщину пластины закладной детали по формуле (207), принимая Rср = 1300 кгс/см2: δп = 0,25dRа/Rср = 0,25·1,8·3400/1300 = 1,18 см. Из условия сварки анкеров под
слоем флюса на автоматах (см. табл. 49) толщина пластины должна
быть не менее 0,65d =
0,65·1,8 = 1,17 см. Принимаем толщину пластины δп = 12 мм. Пример
49. Дано: к
закладной детали колонны приварены элементы стальных связей, работающие на
растяжение (узел примыкания элементов и усилия в них - по рис. 74);
анкеры закладной детали из арматуры класса А-III (Rа = 3400 кгс/см2);
бетон марки М 400 (Rр = 13
кгс/см2). Требуется запроектировать
анкеры закладной детали, определить толщину закладной детали и проверить
выкалывание бетона. Расчет. Принимаем расположение
анкеров как показано на рис. 74. Рис. 74. К примеру расчета 49 Усилие в раскосе раскладываем
на нормальную силу, приложенную к закладной детали с эксцентрицитетом e0 = 5 см, и сдвигающую силу Q: N = 28cos43°45' + 15,9 = 36,29 тс; Q = 28sin 43°45' = 19,35 тс. При z = 42 см и M = Ne0 = 36,29·0,05 = 1,8 тс·м определяем наибольшее
растягивающее усилие в одном ряду анкеров по формуле (201):
Наибольшее сжимающее усилие в
одном ряду анкеров вычисляем по формуле (203):
Сдвигающее усилие Qан, приходящееся на один ряд
анкеров, определяем по формуле (202), принимая N'ан = 0: Qан =
Q/nан =
19,35/4 = 4,84 тс. Так как N'ан
< 0, то ω = 0,6N/Q = 0,6·36,29/19,35 = 1,12. Отсюда
Задаваясь диаметром анкеров
12 мм, по табл. 26 при марке бетона М 400 и анкерах из арматуры
класса А-III находим k = 0,57. Тогда
Принимаем три анкера в каждом
ряду диаметром 16 мм (Fан = 6,09 см2). Проверим необходимое значение
Fан при коэффициенте k, соответствующем принятому
диаметру 16 мм, т.е. при k =
0,52:
Окончательно принимаем три
анкера Æ18 мм (Fа = 7,63 см2).
Необходимая толщина пластины из условия прочности (207) равна δп = 0,25dRа/Rср = 0,25·18·3400/1300 = 11,8 мм. Из условия сварки в отверстия
с раззенковкой (см. табл. 49) δп = 0,75d = 0,75·18 = 13,5 мм.
Принимаем δп = 14 мм. Принятые расстояния между
осями анкеров вдоль и поперек сдвигающей силы, соответственно равные 14 см
>6dр = 6·1,8 = 12,8 см и 9 см
> 4d = 4·1,8 = 7,2 см,
удовлетворяют требованиям рис. 128. Концы анкеров привариваем к
аналогичной закладной детали, расположенной на противоположной грани колонны. Проверяем бетон на
выкалывание согласно п. 3.107. Поскольку N'ан < 0 и концы анкеров имеют усиления, проверяем
условие (209). Определяем площадь проекции
поверхности выкалывания П (см.
рис. 74)
за вычетом части площади закладной детали Fз.д,
расположенной на
поверхности выкалывания: Fз.д = (50 - 2·5)26 = 1040 см2; a1 = 40 + 2·38,6 = 117,2
см; a2 = 60 см; П = a1a2 - Fз.д = 117,2·60 - 1040 = 6000 см2. Поскольку сила N приложена в центре тяжести площади П, e1 = e2 = 0. 0,5ПRр
= 0,5·6000·13 = 39000 кгс = 39 тс > N = 36,29 тс, т.е. прочность бетона на выкалывание обеспечена. Расчет стыков сборных колонн
3.110. Стыки колонн, выполняемые путем ванной сварки выпусков продольной
арматуры, расположенных в специальных подрезках, при последующем
замоноличивании этих подрезок (см. п. 5.94), рассчитываются для двух
стадий работы: а) до замоноличивания стыка -
на нагрузки, действующие на данном этапе возведения здания; при определении
усилий такие стыки условно принимаются шарнирными; б) после замоноличивания
стыка - на нагрузки, действующие на данном этапе возведения здания и при
эксплуатации; при определении усилий такие стыки принимаются жесткими. 3.111.
Расчет незамоноличенных стыков колонн,
указанных в п. 3.110 (рис. 75), производится на местное сжатие бетона колонны центрирующей прокладкой
из условия (184) с добавлением в его правую часть усилия, воспринимаемого арматурными
выпусками и равного Nвып = 0,5φRа.сFа, (217) где φ - коэффициент
продольного изгиба для выпусков, определяемый в соответствии с главой СНиП по
проектированию стальных конструкций при расчетной длине l0. равной фактической длине
сварных выпусков; Fа - площадь сечения всех выпусков. При этом значение R*см умножается на коэффициент
μсм = 0,75, учитывающий неравномерность распределения нагрузки
под центрирующей прокладкой, а за расчетную площадь Fр принимается площадь ядра
сечения торца колонны Fя с размерами, не превышающими
соответствующих утроенных размеров площади смятия Fсм. За площадь Fсм принимается площадь
центрирующей прокладки или, если центрирующая прокладка приваривается на
монтаже к распределительному листу (рис. 75), то за Fсм принимается площадь этого
листа; при этом его учитываемые в расчете размеры не должны превышать
соответствующих размеров площади Fя, а толщина листа должна быть
не менее 1/3 максимального расстояния от края листа до
центрирующей прокладки. Рис. 75. Незамоноличенный
стык колонны 1 - центрирующая прокладка; 2 - распределительный лист; 3
- ванная сварка арматурных выпусков; 4 - сетки косвенного армирования торца
колонны Рис. 76. Расчетное сечение
замоноличенного стыка колонны с косвенным армированием как в бетоне колонны, так
и в бетоне замоноличивания 1 - бетон колонны; 2 - бетон
замоноличивания; 3 - сетки косвенного армирования 3.112.
Расчет замоноличенных стыков колонн, указанных
в п. 3.110, производится как для сечения колонны на участке с подрезками, согласно
пп. 3.59 - 3.78, с учетом следующих указаний: а) при наличии косвенного
армирования сетками как в бетоне колонны, так и в бетоне замоноличивания расчет
ведется согласно пп. 3.60 и 3.62, при этом рассматривается
цельное сечение, ограниченное стержнями сеток, расположенными у граней
замоноличенного участка колонны (рис. 76); б) при наличии косвенного
армирования только в бетоне колонны расчет производится либо с учетом этого
косвенного армирования, но без учета бетона замоноличивания, либо с учетом
бетона замоноличивания, но без учета косвенного армирования колонны; прочность
стыка считается обеспеченной при выполнении условия прочности хотя бы по одному
из этих расчетов; в) расчетные сопротивления
бетона колонн и бетона замоноличивания (Rпр или R*пр) умножаются на коэффициенты
условий работы, соответственно равные mбк = 0,9 и mбз = 0,8; г) при расчете с учетом
замоноличивания значение ξ0 определяется по формуле (19) или
(90)
по марке бетона замоноличивания, если он располагается по всей ширине наиболее
сжатой грани, и по наибольшей марке бетона, если по сжатой грани располагается
частично бетон замоноличивания и частично бетон колонны; в формуле (90)
всегда учитывается минимальное значение μкс. При расчете стыка с учетом
бетона замоноличивания площадь сечения замоноличивания Fз рекомендуется приводить к
площади сечения колонны путем умножения ее на отношение расчетных сопротивлений
бетона замоноличивания и бетона колонны при неизменных высотах сечения
замоноличивания. Для симметрично-армированных
колонн прямоугольного сечения расчет замоноличенного стыка можно производить по
формулам пп. 3.69
и 3.70,
принимая за h'п = hп высоту сечений подрезок, а
за b'п = bп - ширину сечения,
приведенного к бетону колонны, по наиболее сжатой стороне сечения. Коэффициент η, учитывающий прогиб колонны
(см. п. 3.57),
определяется по геометрическим характеристикам сечения колонны вне зоны стыка. 3.113. Стыки колонн, осуществляемые
насухо без замоноличивания (сферические стыки колонн, стыки с приторцованными
поверхностями и т.п.), рассчитываются с учетом косвенного армирования согласно
пп. 3.60
и 3.62,
и коэффициента условий работы 0,65, вводимого на расчетное сопротивление бетона
R*пр. Примеры расчета
Пример
50. Дано:
стык колонны приведен на рис. 77; бетон колонны марки М 400 (Rкпр = 150 кгс/см2 при
mб1 = 0,85); бетон
замоноличивания марки М 300 (Rзпр = 115 кгс/см2 при
mб1 = 0,85); арматурные выпуски
класса А-III (Rа = Rа.с = 3400 кгс/см2)
площадью сечения Fа = F'а = 40,7 см2 (4Æ36); сетки косвенного армирования из стержней класса А-III диаметром 8 мм расположены с шагом s1 = 7 см как в бетоне колонны,
так и в бетоне замоноличивания; продольная сила в стадии эксплуатации N = 390 тс, ее эксцентрицитет в
перпендикулярном к подрезкам направлении с учетом прогиба колонны e0 = 5,5 см. Требуется проверить прочность
стыка в стадии эксплуатации и определить предельную продольную силу в стыке в
стадии возведения здания. Расчет в
стадии эксплуатации В соответствии с п. 3.112
«а» принимаем размеры сечения по осям крайних стержней сеток, т.е. b = h = 36 см;
h0 = 33 см (см. рис. 77). Определим расчетные
сопротивления бетона колонны и замоноличивания с учетом сеток косвенного
армирования согласно п. 3.60. Для бетона колонн: Fкя =
36·20 = 720 см2
(см. рис. 77); n1 =
5; l1 = 17; n2 = 3; l2 =
36; fс1 = fс2 = 0,503 см2 (Æ8);
Отсюда значение R*кпр, с учетом коэффициента условий
работы mкб = 0,9 (см. п. 3.112
«в»), равно: R*кпр = mкб(Rпр + kμскRса) = 0,9(150 +
1,84·0,0193·3400) = 243 кгс/см2. Рис. 77. К примеру расчета 50 1 - арматурные выпуски; 2 - распределительный лист; 3
- центрирующая прокладка Для бетона замоноличивания в
одной из подрезок: Fзя = 36·8 = 288 см2 (см. рис. 77); fс1 = fс2 = 0,503 см2 (Æ8); l1 = 6,5 см; l2 = 36 см;
Значение R*зпр с учетом коэффициента
условия работы mзб
= 0,8 равно R*зпр = mзб(Rпр + kμскRса) = 0,8(115 +
1,29·0,026·3400) = 183,4 кгс/см2. Определим значение ξ0
по формуле (90)
по марке бетона замоноличивания, поскольку подрезка располагается по всей
ширине наиболее сжатой грани колонны; при этом принимаем минимальное значение μск = 0,0193:
принимаем ξ0 = 0,85 - 0,0008Rпр + Принимаем ξ0
= 0,9. Приводим сечение стыка к
бетону колонны, при этом ширина подрезки становится равной b'п = bR*зпр/R*кпр
= 3·183,4/243 = 27,2 см. а высота подрезки h'п = 8 см (см. рис. 77). Прочность стыка проверяем
согласно п. 3.69. Для этого по формуле (18)
определим значение ξR,
принимая σε = 5000 кгс/см2:
Fсв = (b'п - b)h'п = (27,2 - 36)8 = -70,4 см2. Высота сжатой зоны равна
Так как x = 46,5 см > ξRh0 = 0,8·33 = 26,4 см, высоту
сжатой зоны определяем по формуле (116). Для этого вычисляем:
Значение e равно e =
e0 +
(h0 -
a')/2 = 5,5 + (33 - 3)/2 = 20,5 см. Прочность стыка проверяем по
условию (115): R*кпрbх(h0 - x/2)
+ R*кпрFсв(h0 - hп'/2)
+ Rа.сF'а(h0 - a') = 243·36·29,9(33 - 29,9/2) -
243·70,4(33 - 8/2) + 3400·40,7(33 - 3) = 83,74 тс·м > 390·0,205 = 80 тс·м, т.е. прочность стыка в стадии эксплуатации
обеспечена. Проверяем условие (91),
обеспечивающее трещиностойкость защитного слоя замоноличенного участка колонны.
Для этого вычисляем площадь и момент инерции полного сечения, приведенного к
бетону колонны. Из таблицы (21)
коэффициент приведения n = 13 для марки бетона М 400
и арматуры класса А-III: bприв = bколRзпр/Rкпр = 40·115/150 = 30,67 см; Fп = 30,67·10·2 + 40·20 +
40,70·13·2 = 2472 см2,
y = h/2 = 40/2 = 20 см.
т.е. трещиностойкость обеспечена. Расчет незамоноличенного
стыка в стадии возведения Определяем расчетное
сопротивление бетона смятию с учетом косвенного армирования согласно пп. 3.97 и 3.111. Площадь ядра сечения торца
колонны, ограниченная контуром сеток, равна Fя = 17·36 = 612 см2. За площадь смятия принимаем
площадь распределительного листа, поскольку его толщина 2 см превышает 1/3
расстояния от края листа до центрирующей прокладки (5/3 =
1,7 см). При этом ширину площади смятия принимаем равной ширине площади Fя - 17 см. Fсм = 20·17 = 340 см2. Поскольку 36 см < 3·20 см,
принимаем Fр = Fя = 612 см2.
Отсюда:
γк = 4,5 - 3,5Fсм/Fр = 4,5 -
3,5·340/612 = 2,56;
Поскольку расчет ведем на
нагрузки в стадии возведения, принимаем Rпр
= 190 кгс/см2 (т.е. при mб1 =
1,1):
Значение R*см определяем по формуле (185),
учитывая коэффициент μ = 0,75: R*см = μ(Rпрγб + kμксRасγк) =
0,75(190·1,22 + 1,92·0,0226·3400·2,56) = 457 кгс/см2. По формуле (217)
определяем усилие в арматурных выпусках. Радиус инерции арматурного
стержня Æ36 равен r = d/4 = 3,6/4 = 0,9 см. Длина сваренных выпусков l = l0 = 40 см. Согласно табл. 53 главы СНиП по проектированию стальных конструкций
(II-В.3-72) λ = l0/r = 40/0,9
= 44,4 для стали класса С52/40 (с R = 3400 кгс/см2
как для класса А-III) находим φ =
0,85. Отсюда Nвып = 0,5φRа.сFа = 0,5·0,85·3400·81,4 =
117,62 тс. Предельная продольная сила,
воспринимаемая незамоноличенным стыком, равна N = R*смFсм + Nвып = 457·340 + 117620 = 273 тс. Расчет бетонных шпонок
3.114. Размеры бетонных шпонок, передающих сдвигающие усилия между сборным
элементом и дополнительно уложенным бетоном или раствором (рис. 78), должны определяться по
формулам: где Qсд - сдвигающая сила, передающаяся через шпонки; δш, hш, lш - глубина,
высота и длина шпонки; nш - число шпонок, вводимое в расчет и принимаемое не более трех. При наличии сжимающей силы N высоту шпонок допускается определять
по формуле и принимать уменьшенной против высоты, определяемой
условием (219)
не более, чем в 2 раза. При соединении шпонками
элементов настила длина шпонки, вводимая в расчет, должна составлять не более
половины пролета элемента; при этом величина Qсд принимается равной сумме сдвигающих усилий по всей
длине элемента. По условиям (218) -
(220)
следует проверять как шпонки сборного элемента, так и шпонки из дополнительно
уложенного бетона, принимая расчетные сопротивления бетона шпонок Rпр и Rр как для бетонных конструкций. Примечание.
При расчете на выдергивание растянутой ветви двухветвевой колонны из стакана
фундамента допускается учитывать работу 5 шпонок. Рис. 78. Обозначения, принятые при
расчете шпонок, передаю щих сдвигающие усилия от сборного элемента монолитному
бетону 1 - сборный элемент; 2 - монолитный бетон 4. РАСЧЕТ ЭЛЕМЕНТОВ
ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ВТОРОЙ ГРУППЫ
РАСЧЕТ
ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО ОБРАЗОВАНИЮ ТРЕЩИН
4.1(4.1). Железобетонные элементы рассчитываются по образованию трещин: нормальных к продольной оси
элемента; наклонных к продольной оси
элемента. Расчет по образованию трещин
производится*: * Для
элементов, указанных в поз. 1 табл. 1 с проволочной арматурой
классов В-I
и Вр-I,
расчет должен обеспечивать от образования трещин при действии полной нагрузки с
коэффициентом перегрузки n > 1. для выявления необходимости
проверки по раскрытию трещин; для выяснения случая расчета
по деформациям. В железобетонном элементе или
на его участках трещины отсутствуют, если усилия, вызванные действием полной
нагрузки или ее части (когда нагрузки вызывают усилия разных знаков), вводимые в расчет с коэффициентом
перегрузки n = 1, меньше усилия, которое воспринимает сечение при
образовании трещин. Полная нагрузка включает постоянные, длительные и
кратковременные нагрузки. Допускается принимать без
расчета, что изгибаемые элементы прямоугольного и таврового со сжатыми полками
сечений имеют на наиболее напряженных участках трещины, нормальные к продольной
оси, если требуемый по расчету коэффициент армирования μ больше 0,005. 4.2(4.2). Для изгибаемых, растянутых и
внецентренно-сжатых железобетонных элементов усилия, воспринимаемые сечениями,
нормальными к продольной оси, при образовании трещин определяются исходя из
следующих положений: сечения после деформации
остаются плоскими; наибольшее относительное
удлинение крайнего растянутого волокна бетона равно
напряжения в бетоне сжатой
зоны (если она имеется) определяются с учетом упругих, а для
внецентренно-сжатых элементов - также с учетом неупругих деформаций бетона; напряжения в бетоне
растянутой зоны распределены равномерно и равны по величине RрII; напряжения в арматуре равны
алгебраической сумме напряжений, вызванных усадкой бетона, и напряжения,
отвечающего приращению деформаций окружающего бетона. 4.3(4.5). Расчет по образованию трещин, нормальных к продольной оси элемента, производится
из условия Mяв ≤ Mт, (221) где Mяв - момент внешних сил, расположенных по одну
сторону от рассматриваемого сечения, относительно оси, параллельной нулевой
линии и проходящей через ядровую точку, наиболее удаленную от растянутой зоны,
трещинообразование которой проверяется; Mт - момент, воспринимаемый сечением, нормальным к продольной оси
элемента, при образовании трещин и определяемый по формуле Mт = RрIIWт ± Mяус. (222) Здесь Mяус - момент усилия Nус, вызванного усадкой бетона,
относительно той же оси, что и для определения Mяв; знак момента определяется
направлением вращения («плюс» - когда направления противоположны, «минус» -
когда направления моментов Mяус и Mяв
совпадают). Для свободно опертых балок и
плит момент Mт определяется
по формуле Mт =
RрIIWт - Nус(eон + rу). (223) Усилие Nус рассматривается как внешняя
растягивающая сила; его величина и эксцентрицитет относительно центра тяжести
приведенного сечения определяются по формулам: Nус = σус(Fа + F'а); (224)
где yа, y'а - расстояние от центра тяжести приведенного сечения
до центров тяжести сечений соответственно арматуры A и A'; σус - напряжение
в арматуре, вызванное усадкой бетона, равное 400 кгс/см2 для бетона
М 400 и ниже при естественном твердении и 350 кгс/см2 для бетона тех
же марок при тепловой обработке; для других марок бетона σус принимается согласно СНиП
II-21-75, табл. 4,
поз. 8. Если коэффициент армирования μ
меньше 0,01 допускается величины Wт и rу определять как для бетонного
сечения, принимая Nус = 0 и Fа =
F'а = 0. Величина Mяв
определяется по формулам: для изгибаемых элементов
(рис. 79,а)
Mяв =
M; для внецентренно-сжатых
элементов (рис. 79,б) - Mяв
= N(e0 - rу); (225) для центрально- и
внецентренно-растянутых элементов (рис. 79,в) - Mяв
= N(e0 + rу). (226) В формулах (222), (223), (225) и
(226): rу - расстояние от центра тяжести приведенного сечения до ядровой
точки, наиболее удаленной от растянутой зоны, трещинообразование которой
проверяется. Величина rу определяется: для изгибаемых элементов по
формуле rу = W0/Fп, (227) для внецентренно-сжатых
элементов по формуле rу = 0,8W0/Fп, (228) для центрально- и
внецентренно-растянутых элементов по формуле
Wт - момент сопротивления приведенного сечения для
крайнего растянутого волокна с учетом неупругих деформаций растянутого бетона,
определяемый согласно указаниям п. 4.4. Примечание.
Приведенное сечение включает сечение бетона, а также сечение всей продольной
арматуры, умноженное на отношение соответствующих модулей упругости арматуры и
бетона. Рис. 79. Схема усилий и эпюры
напряжений в поперечном сечении элемента при расчете его по образованию трещин,
нормальных к продольной оси элемента а -
при изгибе; б - при
внецентренном сжатии; в -
при внецентренном растяжении; 1 - ядровая точка; 2 - центр тяжести
приведенного сечения 4.4(4.7). Величина момента сопротивления приведенного сечения для крайнего
растянутого волокна с учетом неупругих деформаций растянутого бетона Wт определяется в предположении
отсутствия продольной силы N по
формуле
где Iб.о, Iа.о, I'а.о - моменты инерции соответственно площадей сечения сжатой зоны
бетона, арматуры A и A' относительно нулевой линии; Sб.р -
статический момент площади растянутой зоны бетона относительно нулевой линии. Положение нулевой линии в
общем случае определяется из условия Sб.о + nS'а.о - nSа.о = (h - x)Fб.р/2, (231) где Sб.о, Sа.о, S'а.о - статические моменты соответственно площадей сечения сжатой зоны
бетона, арматуры A и A' относительно нулевой линии; Fб.р - площадь сечения растянутой зоны бетона. Для прямоугольных, тавровых и
двутавровых сечений условие (231) принимает вид
где
Значение Wт допускается определять по
формуле Wт = [0,292 + 0,75(γ1 + 2μ1n) + 0,075(γ'1 + 2μ'1n)]bh2, (233) где
При известном значении W0 (см. п. 4.3)
величину Wт можно также определить по формуле Wт = γW0, (234) где γ - см. табл. 27. 4.5. Участки по длине изгибаемого элемента, на которых отсутствуют наклонные
трещины, определяются из условия Q ≤ 0,6RрIIbh0. (235) Для сплошных плоских плит
правая часть условия (235) увеличивается на 25 %. Таблица 27
РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ
ЭЛЕМЕНТОВ ПО РАСКРЫТИЮ ТРЕЩИН
4.6.(4.13). Железобетонные элементы рассчитываются по раскрытию трещин: нормальных к продольный оси
элемента; наклонных к продольной оси
элемента. Проверка ширины раскрытия
трещин не требуется, если, согласно расчету по пп. 4.1 - 4.5, они не образуются от
действия постоянных, длительных и кратковременных нагрузок, вводимых в расчет с
коэффициентом перегрузки n = 1. Для изгибаемых и
внецентренно-сжатых элементов, указанных в табл. 1 (поз. 4) и входящих в состав
статически определимых систем, при однорядном армировании проверка ширины
раскрытия нормальных трещин не требуется в следующих случаях: а) если коэффициент
армирования μ превышает: для арматуры классов В-I, Вр-I и А-I - 0,01; для арматуры классов А-II и А-III - 0,02; б) если при любых
коэффициентах армирования μ диаметр арматуры не
превышает: для арматуры классов А-I и А-II - 22 мм; для арматуры класса А-III - 8 мм. При расчете по раскрытию
трещин усилие от усадки бетона Nус принимается равным нулю. 4.7. В общем случае расчет по раскрытию трещин производится два раза: на
кратковременное и на длительное раскрытие трещин (см. п. 1.16). Для изгибаемых элементов,
указанных в табл. 1 (поз. 4), а также эксплуатируемых ниже уровня
грунтовых вод (поз. 2), допускается расчет производить только один раз: а) при проверке раскрытия
трещин, нормальных к продольной оси элемента: если Mдл/Mп ≥ 2/3, проверяется длительное раскрытие
трещин от действия момента Mдл; если Mдл/Mп < 2/3, проверяется кратковременное раскрытие
трещин от действия момента Mп; б) при проверке раскрытия
трещин, наклонных к продольной оси элемента: если (Qдл/Qп)2 ≥ 2/3, проверяется длительное
раскрытие трещин от действия поперечной силы Qдл; если (Qдл/Qп)2 < 2/3, проверяется кратковременное
раскрытие трещин от действия поперечной силы Qп. Здесь Qдл и Qп - соответственно наибольшая
поперечная сила на рассматриваемом участке элемента с постоянным насыщением
поперечной арматурой от постоянных и длительных нагрузок и от полной нагрузки
(вводимых в расчет с коэффициентом перегрузки n = 1). Расчет по раскрытию
трещин, нормальных к продольной оси элемента
4.8.(4.14). Ширина раскрытия трещин, нормальных к продольной оси элемента, aт, мм, должна определяться по формуле aт = kcдη где k -
коэффициент, принимаемый равным: для изгибаемых и внецентренно-сжатых элементов
- 1; для растянутых элементов - 1,2; cд -
коэффициент, принимаемый равным при учете: кратковременных нагрузок и
кратковременного действия постоянных и длительных нагрузок - 1; длительного действия
постоянных и длительных нагрузок для конструкций из бетонов: естественной
влажности - 1,5; в водонасыщенном состоянии (элементы, воспринимающие давление
жидкостей, а также эксплуатируемые в грунте ниже уровня грунтовых вод) - 1,2; η - коэффициент, принимаемый равным: при стержневой арматуре: периодического профиля - 1; гладкой - 1,3; при проволочной арматуре: периодического профиля -
1,2; гладкой - 1,4; σа - напряжение
в стержнях крайнего ряда арматуры A,
определяемое
согласно указаниям п. 4.10;
значение если hп < a, то
растянутые свесы при вычислении если во
внецентренно-растянутых элементах сила N расположена между центрами тяжести арматуры A и A', то при определении
где Fа - площадь
всей продольной арматуры; d - диаметр растянутой арматуры, мм; при различных диаметрах
стержней значение d принимается равным
d1,
…, dк - диаметр стержней растянутой
арматуры; n1,
…, nк - число стержней с диаметрами
соответственно d1, …, dк. При пользовании формулой (236)
значения aт и d принимаются в мм. Кроме
того, следует учитывать указания п. 4.9. 4.9(4.14). Ширина раскрытия трещин aт, определенная согласно
указаниям п. 4.8, корректируется в следующих случаях: а) Если центр тяжести сечения
стержней крайнего ряда арматуры A изгибаемых,
внецентренно-сжатых, внецентренно-растянутых при e0 ≥ 0,8h0 элементов отстоит от наиболее растянутого волокна
бетона на расстоянии c, большем 0,2h, величина aт, определенная по формуле (236),
должна умножаться на коэффициент kс, равный
и принимаемый не более 3. б) Для слабоармированных
изгибаемых элементов (например, фундаментов) при kб = kнkд, (240) но не более 1, где kн - коэффициент, учитывающий уровень нагружения, равный
10 - сжимающее напряжение, кгс/см2; kд - коэффициент, учитывающий длительность действия нагрузки,
равный: при кратковременном действии
нагрузки - 1, при длительном действии
нагрузки kд = 1,5Mт/Mп, но не менее единицы; M0 -
момент, при котором растянутый бетон над трещинами практически выключается из
работы, равный
но не более 2,5
η - см. п. 4.8. При использовании
коэффициента Kб и при Mдл/Mп < 2/3 не следует
пользоваться рекомендациями п. 4.7 «а». в) Для статически
неопределимых изгибаемых элементов, а также для свободно опертых балок при l/h < 7, и консолей при l1/h < 3,5, где l1 - вылет консоли, вблизи мест
приложения сосредоточенных сил и опорных реакций при μ ≤ 0,02 ширину
раскрытия трещин aт, вычисленную по формуле (236),
допускается уменьшить путем умножения на коэффициент kм, учитывающий местные
особенности напряженного состояния в железобетонных конструкциях и определяемый
по формуле
но не менее 0,8 и не более 1, где a -
расстояние от точки приложения сосредоточенной силы или опорной реакции до
рассматриваемого сечения, принимаемое не более 0,3h (рис. 80); Рис. 80. Положение опорных
реакций в жестких узлах, принимаемое для определения коэффициента Kм а - г - стыки сборных элементов; д - з - монолитные
сопряжения P -
абсолютное значение сосредоточенной силы или реакции; M -
абсолютное значение изгибающего момента в нормальном сечении, проходящем через
точку приложения сосредоточенной силы или опорной реакции (рис. 80); h - расстояние от грани элемента, к которой приложена
сила P, до растянутой
грани; h0 - то же, до растянутой арматуры (рис. 81). Рис. 81. Обозначения величин h0 и h для определения коэффициента kм а -
при приложении силы к сжатой грани элемента; б - при приложении силы к уширениям (полкам) элемента; в -
по длине статически неопределимой балки 4.10(4.15). Напряжения в растянутой арматуре σа должны определяться по формулам: для центрально-растянутых
элементов σа = N/Fа; (243) для изгибаемых элементов σа = M/(Fаz1); (244) для внецентренно-сжатых, а
также внецентренно-растянутых при e0 ≥ 0,8h0 элементов В формуле (245)
знак «+» принимается при внецентренном растяжении, а знак «-» - при
внецентренном сжатии. Для внецентренно-растянутых
элементов при e0 < 0,8h0 величину σа следует определять по
формуле (245),
принимая z1 равным zа - расстоянию между центрами
тяжести арматуры A и A'. При этом если растягивающая
продольная сила расположена между центрами тяжести арматуры A и A', значение eа в формуле (245)
принимается со знаком «минус». z1 - расстояние от центра тяжести площади сечения
арматуры A до точки
приложения равнодействующей усилий в сжатой зоне сечения над трещиной,
определяемое согласно указаниям п. 4.16, при этом коэффициент v принимается всегда как при
кратковременном действии нагрузки. Для внецентренно-сжатых
элементов в случае, когда Mяв < Mт (здесь Mяв определяется согласно п. 4.3 от
постоянных и длительных нагрузок), но при действии полной нагрузки трещины
образуются, величина σа определяется по формуле В формуле (246): σа.т - напряжение в
арматуре при действии нагрузки, соответствующей моменту образования трещин,
определяемое по формуле (245); при этом эксцентрицитет eа продольной силы N равен
где yа - расстояние от центра тяжести приведенного сечения до центра
тяжести площади сечения арматуры A; 10 - сжимающее напряжение, кгс/см2; Wт, rу - см. п. 4.3. При расположении растянутой
арматуры в несколько рядов по высоте сечения в изгибаемых, внецентренно-сжатых,
а также внецентренно-растянутых при e0 ≥ 0,8h0 элементах напряжения σа должны умножаться на
коэффициент φп, равный где x = ξh0; величина ξ определяется по формуле (264);
для изгибаемых элементов допускается принимать x таким
же, как и при расчете по прочности; a и c -
расстояние от центра тяжести площади сечения арматуры A соответственно всей и крайнего ряда
стержней до наиболее растянутого волокна бетона. Величина напряжения σа от действия полной нагрузки,
определенная с учетом коэффициента φп не должна превышать RаII - для стержневой и 0,8RаII - для проволочной арматуры; это условие допускается
не проверять для статически определимых конструкций с арматурой одного класса
при ее однорядном расположении. Упрощенные способы
определения σа Для изгибаемых элементов
допускается определять σа по формуле σа = RаM/Mпр. (248) При применении арматуры
разных классов в формулу (248) вводится Rа - расчетное сопротивление
арматуры для предельных состояний первой группы по более прочной арматуре. Здесь Mпр -
предельный момент по прочности, равный: при проверке прочности
сечений - правой части неравенств (17) - (21),
(27),
(28),
(30); при подборе сечения арматуры
где Mрасч - момент от
действия полной нагрузки с коэффициентом перегрузки n > 1; Fа.факт - фактическая площадь принятой арматуры; Fа.теор - площадь арматуры, требуемая по расчету прочности. Для внецентренно-сжатых
элементов при Mяв ≥ Mт допускается вычислять σа по формуле где kт - коэффициент, определяемый
по табл. 28. Найденные по формулам (248) и
(249)
значения σа в случае расположения арматуры в несколько рядов по
высоте сечения умножаются на коэффициент φп определяемый по формуле (247). 4.11(4.14). Ширина кратковременного раскрытия трещин от действия полной нагрузки
определяется как сумма ширины раскрытия от длительного действия постоянных и
длительных нагрузок и приращения ширины раскрытия от действия кратковременной
нагрузки по формуле aт = aт1 - aт2 + aт3, (250) где aт1 - ширина
раскрытия трещин от кратковременного действия полной нагрузки; aт2 - начальная ширина раскрытия трещин от постоянных и длительных
нагрузок (при их кратковременном действии); aт3 - ширина длительного раскрытия трещин от действия постоянных и
длительных нагрузок. В изгибаемых элементах кратковременное
раскрытие трещин от полной нагрузки может определяться по формуле aт = aт1 [1 + (cд - 1)Mдл/Mп], (251) где cд - см. п. 4.8 для
случая длительного действия нагрузок. Если величина aт1 определена с учетом формулы
(240),
то в равенстве (251) коэффициент cд заменяется произведением cдkд, где kд определяется согласно п. 4.9. Ширина длительного раскрытия
трещин определяется от длительного действия постоянных и длительных нагрузок по
формуле (236). Таблица 28
Расчет по раскрытию
трещин, наклонных к продольной оси элемента
4.12(4.17). Ширина раскрытия трещин, наклонных к продольной оси элемента, aт, мм, для изгибаемых
элементов, армированных поперечной арматурой, должна определяться по формуле aт = cдk(h0 + 30dмакс) где cд, η - обозначения те же, что в
формуле (236); k = (20 - 1200μп)103, (253) но не менее 8·103; dмакс - наибольший из диаметров хомутов и отогнутых стержней; при этом в
сумме (h0 + 30dмакс) величины h0 и dмакс - в мм; μп - коэффициент насыщения балки поперечной арматурой, равный μп = μх
+ μо, (254) здесь μх - коэффициент насыщения
балки хомутами: μх = Fх/(bu); (255) μо - коэффициент насыщения балки отогнутыми стержнями: μо = Fо/(buо), (256) uо - расстояние между плоскостями отгибов (наклонных стержней),
измеренное по нормали к ним; при разных расстояниях между отгибами (рис. 82)
величина uо определяется, как полусумма
расстояний между рассматриваемой плоскостью отгибов и двумя соседними с ней
плоскостями отгибов, измеренных по нормали к отгибам: Рис. 82. Учет поперечной и
отогнутой арматуры при расчете железобетонной балки по раскрытию наклонных
трещин а - конструкция балки; б - эпюра насыщения балки отгибами μо;
в - эпюра насыщения
балки поперечными стержнями μк; г - эпюра поперечных сил
Q для первой от опоры плоскости
отгибов uо = (uо1 + uо2)/2; (257) для второй от опоры
плоскости отгибов uо = (uо2 + uо3)/2; (258) для последней (n-й) плоскости отгибов
величина uо принимается
равной расстоянию между ней и предыдущей плоскостью отгибов, т.е. uо = uоn; отгибы могут учитываться в
расчете лишь на тех участках, где расстояние от грани опоры до начала первого
отгиба (u1),
а также расстояние между концом
предыдущего и началом следующего отгиба (u2, u3) не превышает 0,2h (рис. 82); Q - наибольшая поперечная сила
на рассматриваемом участке с постоянным насыщением поперечной арматурой. При расчете рассматриваются
сечения, расположенные на расстояниях от свободной опоры, не меньших h0. Для свободно опертых
элементов, нагруженных равномерно распределенной нагрузкой, рассматривается
сечение на расстояние h0 от опоры. При этом если p фактически
является сплошной равномерно распределенной нагрузкой (например,
гидростатическое давление, давление грунта и т.д.), значение Q принимается равным Q = Qмакс - ph0, (260) если нагрузка фактически может отсутствовать на
участке пролета (например, нагрузка на перекрытие), Q принимается равным Qмакс. Здесь Qмакс - максимальная поперечная
сила у опоры от принятой в расчете равномерно распределенной нагрузки p. При определении
кратковременного и длительного раскрытия трещин должны учитываться указания п. 4.11;
при этом в формуле (251) отношение Mдл/Mп заменяется на (tдл/tп)2, где tдл, tп - величина t, определенная по формуле (259), соответственно от постоянных и длительных
нагрузок и от полной нагрузки. Допускается уменьшать величину
aт в 1,5 раза против определенной по формуле (252),
если балка заармирована поперечными стержнями, нормальными к оси элемента, и
продольными стержнями того же диаметра и с расстояниями по высоте сечения,
равными шагу поперечных стержней. Примеры расчета
Пример
51. Дано:
железобетонная плита перекрытия с размерами поперечного сечения (для половины
сечения плиты) по рис. 83; b =
8,5 см; h = 40 см; bп = 72,5 см; h'п = 5 см; бетон марки М 300;
рабочая арматура класса А-III (Rа: = 3400 кгс/см2, Eа = 2·106 кгс/см2)
расположена в два ряда (a =
5,8 см, c = 3,3 см); площадь ее
сечения Fа = 7,6 см2 (2Æ22); полный момент в
середине пролета
Mп = 6,9 тс·м; вся нагрузка -
длительная; из расчета по прочности известно: Mпр = 8,6 тс·м; x = 3 см. Требуется произвести расчет
по раскрытию трещин, нормальных к продольной оси элемента. Расчет. h0 = h - a =
40 - 5,8 = 34,2 см. Так как μ = Fа/(bh0) = 7,6/(8,5·34,2) = 0,0262 > 0,005, то согласно
п. 4.1,
элемент работает с трещинами в растянутой зоне. Для определения длительного
раскрытия трещин вычисляем напряжение в арматуре σа. Рис. 83. Сборная
железобетонная плита перекрытия Согласно формуле (248),
величина σа на уровне центра тяжести арматуры равна: σа = RаM/Mпр = 3400·6,9/8,6 = 2730 кгс/см2. Поскольку арматура
расположена в два ряда, вычисляем по формуле (247) коэффициент φп:
Напряжение в нижнем стержне
арматуры равно σа = 2730·1,08 = 2940 кгс/см2. Ширину раскрытия трещин
находим по формуле (236). Так как μ =
0,0262 > 0,02, то значение aт = cдkη что меньше предельно допустимой ширины раскрытия
трещин aт = 0,3 мм. Пример
52. Дано:
железобетонная плита фундамента с размерами поперечного сечения h = 30 см; b = 115 см; h0 = 26,5 см; бетон марки М 200
(RрII = 11,5 кгс/см2, Eб = 2,15·105 кгс/см2);
рабочая арматура класса А-III (Rа = 3400 кгс/см2, Eа = 2·106 кгс/см2),
площадь ее сечения Fа = 4,71 см2 (6Æ10); момент в расчетном сечении от постоянных и длительных нагрузок Mдл = 3,2 тс·м, от
кратковременных нагрузок Mкр = 0,5 тс·м; предельный
момент по прочности Mпр = 4,1 тс·м; фундаментная
плита находится ниже уровня грунтовых вод. Требуется произвести расчет
по раскрытию трещин, нормальных к продольной
оси элемента. Расчет. Определяем необходимость
вычисления ширины раскрытия трещин согласно п. 4.6. Для этого находим момент
трещинообразования Mт. Так как μ = Fа/(bh0) = 4,71/(115·26,5) = 0,0016 < 0,01, то момент Mт находим как для бетонного
сечения, используя формулу (233): Mт = RрIIWт
= 0,292bh2RрII = 0,292·115·302·11,5
= 3,45 тс·м. Так как Mт < Mп = 3,2 + 0,5 = 3,7 тс·м, то
проверка ширины раскрытия трещин необходима. Поскольку Mдл/Mп = 3,2/3,7 = 0,865 > 2/3 = 0,67, то, согласно п. 4,7 «а»,
допускается производить расчет только на длительное раскрытие трещин от момента
Mдл. Определение aт производим по формуле (236).
Для этого вычисляем напряжение в арматуре σа. Согласно формуле (248) σа = RаMдл/Mпр = 3400·3,2/4,1 = 2660 кгс/см2. Поскольку фундамент находится
ниже уровня грунтовых вод, то cд = 1,2. Так как
рассматривается изгибаемый элемент прямоугольного сечения с арматурой
периодического профиля, то, согласно п. 4.8, коэффициенты k = 1; η =
1; μ = aт = kcдησа/Eа·20(3,5
- 100 что больше допустимого значения aт.дл = 0,2 мм (см. табл. 1). В
связи с этим требуется более точное определение величины aт согласно указаниям п. 4.9 «б».
Для этого вычисляем коэффициент kб: μn = μ M = Mдл = 3,2 тс·м;
где 10W0 = 10bh2/6 = 10·115·302/6
= 1,73·105 кгс·см; kд = 1,5Mт/Mп = 1,5·3,45/3,7 = 1,4; kб = kнkд = 0,61·1,4 = 0,855. С учетом коэффициента kб расчетная ширина раскрытия
трещин равна aт = 0,23·0,855 = 0,197 мм <
0,2 мм, т.е. ширина раскрытия трещин меньше предельно допустимой. Пример
53. Дано:
железобетонная колонна промышленного здания с размерами поперечного сечения: h = 50 см; b = 40 см; a = a' = 5
см; бетон марки М 200 (RрII = 11,5 кгс/см2, Eб = 2,15·105 кгс/см2);
рабочая арматура класса А-III (Eа = 2·106 кгс/см2) площадью
сечения Fа = F'а = 12,32 см2 (2Æ28); продольная сжимающая сила N = 50 тс; момент от полной нагрузки Mп = 24 тс·м, в том числе момент от постоянных и
длительных нагрузок Mдл = 15 тс·м. Требуется рассчитать колонну
по раскрытию трещин. Расчет. h0 =
h - a = 50 - 5 = 45 см. Определяем необходимость расчета по раскрытию трещин.
Для этого проверяем условие (221). Так как μ = Fа/(bh0) = 12,32/(40·45) = 0,0069
< 0,01, то, согласно п. 4.3, момент образования трещин и величину rу находим как для бетонного
сечения. Согласно формуле (233), Mт = 0,292bh2RрII = 0,292·40·502·11,5
= 3,37 тс·м. Величина rу для элемента прямоугольного
сечения в соответствии с формулой (228) равна rу = 0,8h/6 = 0,8·50/6 = 6,67 см. Эксцентрицитет силы N относительно центра тяжести сечения
при действии момента Mп равен e0 = Mп/N = 24·105/50·103 = 48 см; N(e0 - rу) = 50000(48 - 6,67) = 20,67 тс·м >
3,37 тс·м, т.е. элемент работает с трещинами в растянутой зоне. Согласно п. 4.6,
необходимо проверить длительное и кратковременное раскрытие трещин. Значение aт при длительном действии
нагрузки находим по формуле (236). Для этого вычисляем напряжение в арматуре σа, используя формулу (249): eа = h/2 - a + Mдл/N = 50/2 - 5 + 15·105/(50·103)= 50 см; μn = μ
По вычисленным значениям γ' = 0,071; μn = 0,064 и eа/h0 = 50/45 = 1,11 находим из табл. 28
значение коэффициента kт: kт = 0,326;
Согласно п. 4.8, k = 1; η = 1; aт = kcдη что меньше предельно допустимого значения длительного
раскрытия трещин aт = 0,3 мм. Переходим к вычислению
кратковременного раскрытия трещин от действия полной нагрузки. Для этого,
согласно п. 4.11,
находим величины aт1, aт2 и aт3. Напряжение в арматуре σа
от действия полной нагрузки определяем по формуле (249): еа = h/2 - a + Mп/N
= 50/2 - 5 + еа/h0 = 68/45 = 1,51. При γ' =
0,071, μn = 0,064 и eа/h0 = 1,51; коэффициент kт, согласно табл. 28,
равен 0,52:
aт1 = kcдη Величина aт3 соответствует длительному
раскрытию трещин и уже найдена - aт3 = 0,19 мм. Величина aт2 = aт3/cд = 0,19/1,5 = 0,127 мм. Кратковременное раскрытие
трещин от действия полной нагрузки определяем по формуле (250): aт = aт1 - aт2 + aт3 = 0,273 - 0,127 + 0,19 =
0,336 мм, что меньше предельно допустимого значения aт = 0,4 мм. Пример
54. Дано:
прогон покрытия таврового сечения с размерами ребра b = 10 см; h =
40 см; h0 = 36 см; бетон марки М 300 (RрII = 15 кгс/см2); поперечная арматура класса
А-III диаметром 6 мм; Fх = 0,283 см2; шаг
стержней на приопорном участке u =
15 см;
поперечная сила у опоры от полной равномерно распределенной нагрузки Qп = 4,54 тс, в том числе от
постоянных и длительных нагрузок Qдл = 3,86 тс. Требуется произвести расчет
по раскрытию трещин, наклонных к продольной оси элемента. Расчет. Согласно п. 4.12,
рассматриваем сечение на расстоянии h0 от свободной опоры.
Поперечную силу в этом сечении принимаем такой же, как и на опоре. Определяем необходимость
расчета ширины раскрытия наклонных трещин. Так как 0,6RрIIbh0 = 0,6·15·10·36 = 3,24 тс
< 4,54 тс, то проверка ширины раскрытия трещин необходима. Поскольку
то, согласно п. 4.7 «б», проверяем длительное
раскрытие трещины от действия поперечной силы Qдл. Величину aт находим по формуле (252):
μп = μх = Fх/(bu) = 0,283/(10·15) = 0,0019 (так как наклонные стержни отсутствуют); k = (20 -
1200μп)103 = (20 - 1200·0,0019)103 =
17,7·103. Согласно пп. 4.12 и 4.8,
коэффициенты cд = 1,5 и η =
1. Сумма (h0 + 30dмакс) равна 360 + 30·6 = 540 мм; aт = cдk(h0 + 30dмакс) что меньше предельно допустимого значения aт = 0,3 мм. РАСЧЕТ ЭЛЕМЕНТОВ
ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ ПО ДЕФОРМАЦИЯМ
4.13(4.22, 4.23). Деформации (прогибы, углы
поворота) элементов железобетонных конструкций надо вычислять по формулам
строительной механики, определяя входящие в них величины кривизны в соответствии
с указаниями пп. 4.14 - 4.20. Величина кривизны
определяется: а) для участков элемента, где
в растянутой зоне не образуются трещины, нормальные к продольной оси элемента,
- как для сплошного тела; б) для участков элемента, где
в растянутой зоне имеются трещины, нормальные к продольной оси, - как отношение
разности средних деформаций крайнего волокна сжатой зоны бетона и продольной
растянутой арматуры к рабочей высоте сечения элемента. Элементы или участки
элементов рассматриваются без трещин в растянутой зоне, если трещины не
образуются при действии постоянных, длительных и кратковременных нагрузок; при
этом нагрузки вводятся в расчет с коэффициентом перегрузки n, равным единице. При расчете по деформациям
усилие от усадки бетона Nус допускается принимать равным
нулю. Определение кривизны
железобетонных элементов на участках без трещин в растянутой зоне
4.14(4.24). На участках, где не образуются нормальные к продольной оси трещины,
полная величина кривизны изгибаемых, внецентренно-сжатых и
внецентренно-растянутых элементов должна определяться по формуле где здесь c - коэффициент, учитывающий влияние длительной
ползучести бетона и принимаемый равным: при действии кратковременных
нагрузок - c = 1; при действии постоянных и
длительных нагрузок: а) в условиях эксплуатации
конструкций при влажности воздуха окружающей среды выше 40 % - c = 2; б) то же, при влажности
воздуха 40 % и ниже - c =
3. Влажность воздуха окружающей
среды принимается согласно указаниям п. 1.3. Определение кривизны
железобетонных элементов на участках с трещинами в растянутой зоне
4.15(4.27). На участках, где образуются нормальные к продольной оси элемента
трещины, кривизны изгибаемых, внецентренно-сжатых, а также
внецентренно-растянутых при e0 ≥ 0,8h0 элементов прямоугольного,
таврового и двутаврового (коробчатого) сечений должны определяться по формуле Для изгибаемых элементов
последнее слагаемое правой части формулы (263) принимается равным нулю;
знак «-» в этой формуле принимается при внецентренном сжатии, а знак «+» - при
внецентренном растяжении. В формуле (263): Mз - момент (заменяющий) относительно оси, нормальной к плоскости
действия момента и проходящей через центр тяжести площади сечения арматуры A, от всех внешних сил, расположенных
по одну сторону от рассматриваемого сечения: для изгибаемых элементов Mз = M; для внецентренно-сжатых и
внецентренно-растянутых элементов Mз = Neа; z1 - расстояние от центра тяжести площади сечения арматуры A до точки приложения равнодействующей усилий в сжатой
зоне сечения над трещиной (плечо внутренней пары сил), определяемое по
указаниям п. 4.16; ψа - коэффициент,
учитывающий работу растянутого бетона на участке с трещинами и определяемый по
указаниям п. 4.17; ψб - коэффициент,
учитывающий неравномерность распределения деформаций крайнего сжатого волокна
бетона по длине участка с трещинами и принимаемый равным 0,9; γ' - коэффициент, определяемый по формуле (267); ξ = x/h0 - определяется
согласно указаниям п. 4.16; v - коэффициент, характеризующий
упругопластическое состояние бетона сжатой зоны и принимаемый равным: при кратковременном действии
нагрузки - v = 0,45; при длительном действии
нагрузки: а) в условиях эксплуатации
конструкций при влажности воздуха
окружающей среды выше 40 % - v =
0,15; б) то же, 40 % и ниже - v = 0,10. Влажность воздуха окружающей
среды принимается согласно указаниям п. 1.3. 4.16(4.28). Величина ξ вычисляется по формуле но не более 1, при этом eа/h0 принимается не менее 0,5. Для изгибаемых элементов
последнее слагаемое правой части формулы (264) принимается равным нулю. В формуле (264)
верхние знаки принимаются при сжимающем, а нижние - при растягивающем усилии N. В формуле (264):
Величина z1 вычисляется по формуле Для элементов прямоугольного
сечения и таврового с полкой в растянутой зоне в формулы (266), (267) и
(269)
вместо величины hп подставляется величина 2a' или h'п = 0, соответственно при наличии или отсутствии
арматуры A'. Если ξ < a'/h0, величины γ', ξ, z1 и 1/ρ следует определять без учета
арматуры A'. Расчет сечений, имеющих полку
в сжатой зоне, при ξ < h'п/h0 производится как прямоугольных шириной b'п. Расчетная ширина полки b'п
определяется согласно указаниям п. 3.24. Для внецентренно-сжатых
элементов величина z1 должна приниматься не более
0,97eа. 4.17(4.29). Величина коэффициента ψа определяется по формуле но не более 1; при этом eа/h0 принимается не менее 1,2/s. Для изгибаемых элементов
последний член в правой части формулы (270) принимается равным нулю. В формуле (270): s - коэффициент, учитывающий
влияние длительности действия нагрузки и принимаемый равным: при кратковременном действии
нагрузки: а) для стержневой арматуры: гладкой - 1; периодического профиля - 1,1; б) для проволочной арматуры - 1; при длительном действии
нагрузки - 0,8; но не более 1. Здесь Wт - см. п. 4.4; Mяв и Mяус - см. п. 4.3;
допускается принимать Mяус = 0. 4.18. Кривизны 1/ρ внецентренно-растянутых
элементов с эксцентрицитетами e0 < 0,8h0 на участках с нормальными трещинами в растянутой зоне определяются по
формуле где zа - расстояние между центрами тяжести площадей арматуры A и A'; ψа и ψ'а - коэффициенты, учитывающие работу растянутого бетона на участке с
трещинами, соответственно для арматуры A и A'. Если сила N приложена между центрами тяжести
площадей арматуры A и A', эксцентрицитет eа в формуле (272)
принимается со знаком «минус». Значения коэффициентов ψа и ψ'а вычисляются по формулам: ψа = 1 - sNт/N; (273) ψ'а = 1 - sN'т/N. (274) Nт - усилие, приложенное в той же точке, что и сила N, соответствующее образованию трещин в более растянутой зоне сечения; N'т - то же, для менее растянутой зоны сечения; s - коэффициент, принимаемый равным: а) при кратковременном
действии нагрузки - s =
0,7; б) при длительном действии
нагрузки - s = 0,35. Отношения Nт/N и N'т/N в формулах (273) и (274) принимаются не более 1.
При эксцентрицитете 0,8h0 > e0 > y - a (где y - расстояние
от более растянутой грани до центра тяжести приведенного сечения) коэффициент
ψ'а определяется по
формуле (274)
при отношении N'т/N равном единице. Значения Nт и N'т определяются по формулам:
где Wт, W'т - значения Wт, определенные согласно п. 4.4,
соответственно для более растянутой и менее растянутой граней сечения; r'у, rу -
расстояние от центра тяжести приведенного сечения до условных ядровых точек,
определенных согласно п. 4.3, наиболее удаленных соответственно от более
растянутой и менее растянутой граней элемента. 4.19. Для элементов прямоугольного
сечения с симметричной арматурой, испытывающих косое внецентренное сжатие,
кривизны вычисляются по формуле где kβ -
коэффициент, учитывающий влияние угла наклона силовой плоскости на величину
деформаций кососжимаемых элементов;
здесь
hх, hу - размер сечения в
направлении осей x и y; β - угол
наклона силовой плоскости (плоскости эксцентрицитета силы N) к плоскости оси x в радианах. Плоскость деформирования
составляет с плоскостью оси x угол
γ, определяемый из равенства tgγ = tgβIх/Iу, (278) где Iх и Iу - соответственно моменты инерции приведенного
сечения относительно осей y и
x. Кривизны в плоскостях x и y при косом внецентренном сжатии равны: 1/ρx = 1/ρ·cosγ; (279) 1/ρу = 1/ρ·sinγ, (280) где 1/ρ определяется по формуле (276). 4.20(4.30). Полная величина кривизны 1/ρ для участка с трещинами в растянутой зоне при одновременном действии
постоянных, длительных и кратковременных нагрузок должна определяться по
формуле 1/ρ = 1/ρ1 - 1/ρ2 + 1/ρ3, (281) где 1/ρ1 -
кривизна от кратковременного действия всей нагрузки, на которую производится
расчет по деформациям согласно указаниям п. 1.19; 1/ρ2 - кривизна от
кратковременного действия постоянных и длительных нагрузок; 1/ρ3 - кривизна от длительного
действия постоянных и длительных нагрузок. Кривизны 1/ρ1, 1/ρ2 и 1/ρ3 определяются по формулам (263), (272) и
(276),
при этом 1/ρ1 и 1/ρ2 вычисляются при величинах ψа и v, отвечающих кратковременному
действию нагрузки, а кривизна 1/ρ3 - при величинах ψа и v, отвечающих длительному
действию нагрузки. Если величины 1/ρ2 и 1/ρ3 оказываются отрицательными,
то они принимаются равными нулю. Определение прогибов
4.21(4.31). Прогиб fM, обусловленный деформацией изгиба, определяется по
формуле где
При определении прогиба в
середине пролета балочных элементов формула (282) может быть приведена к
виду где
n -
четное число равных участков, на которое разбивается пролет элемента; число n рекомендуется принимать не менее 6. В формулах (282) и
(283)
кривизны 1/ρ определяются по формулам (261) и (281)
соответственно для участков без трещин и с трещинами; знак 1/ρ
принимается в соответствии с эпюрой кривизны. При определении прогибов
статически неопределимых конструкций рекомендуется учитывать перераспределение
моментов, вызванных образованием трещин и неупругими деформациями бетона. Для изгибаемых элементов
постоянного сечения, имеющих трещины, на каждом участке, в (пределах которого
изгибающий момент не меняет знака, кривизну допускается вычислять для наиболее
напряженного сечения, принимая кривизну для остальных сечений такого участка
изменяющейся пропорционально значениям изгибающего момента (рис. 85). Рис. 84. Эпюра кривизны в
железобетонном элементе с переменным по длине сечением Рис. 85. Эпюры изгибающих
моментов и кривизны в железобетонном элементе постоянного сечения а - схема расположения нагрузки; б - эпюра изгибающих моментов; в - эпюра кривизны 4.22(4.32). Для изгибаемых элементов при
l/h < 10 необходимо учитывать влияние поперечных сил на их прогиб. В
этом случае полный прогиб f
равен сумме прогибов, обусловленных соответственно деформацией изгиба fM и деформацией сдвига fQ. 4.23(4.33). Прогиб fQ, обусловленный деформацией
сдвига, определяется по формуле где γс(x) - деформация сдвига, определяемая по формуле
здесь Q(x) - поперечная сила в сечении x от действия внешней нагрузки; G - модуль сдвига бетона (см. п. 2.12); β(x) - коэффициент, учитывающий влияние трещин на
деформации сдвига и принимаемый равным: на участках по длине
элемента, где отсутствуют нормальные и наклонные к продольной оси элемента
трещины, - 1; на участках, где имеются
только наклонные к продольной оси элемента трещины, - 4,8; на участках, где имеются
только нормальные или нормальные и наклонные к продольной оси элемента трещины,
- по формуле M(x) и c -
коэффициент, учитывающий влияние длительной ползучести бетона и принимаемый по
п. 4.14. 4.24(4.34). Для сплошных плит толщиной менее 25 см, армированных плоскими сетками,
с трещинами в растянутой зоне значения прогибов, подсчитанные по формуле (282), умножаются на коэффициент Определение продольных
деформаций
4.25. Относительные деформации ε0 (удлинения или
укорочения) в направлении продольной оси элементов определяются следующим
образом. Относительные деформации
изгибаемых, внецентренно-сжатых и внецентренно-растянутых элементов с
двузначной эпюрой напряжений в сечении определяют: а) для элементов или их
отдельных участков, не имеющих трещин в растянутой зоне, по формуле
где c - см. п. 4.14; V - см. п. 4.15; б) для участков элементов,
указанных в п. 4.15,
имеющих трещины в растянутой зоне, по формуле
где εа.с, εб.с - соответственно средние
величины относительного удлинения арматуры и относительного укорочения крайнего
сжатого волокна бетона на участке между трещинами, определяемые по формулам:
в) для участков
внецентренно-растянутых элементов при e0 < 0,8h0 по формуле
где Mз, ψа, ψ'а, ψб, γ', ξ, z1, zа - см. пп. 4.15 - 4.18. Относительные деформации
внецентренно-сжатых и внецентренно-растянутых элементов с однозначной эпюрой
напряжений определяют: а) для внецентренно-сжатых
элементов или их отдельных участков, не имеющих трещин в растянутой зоне, по
формуле б) для участков
внецентренно-сжатых элементов, в которых от действия полной нагрузки образуются
трещины в растянутой зоне, ε0 находится по формуле (293) с
последующим увеличением на 20 %; в) для
внецентренно-растянутых элементов или их участков при отсутствии трещин
г) то же, при наличии трещин
где εа.с
и ε'а.с -
соответственно средние величины удлинения арматуры A и A', определяемые по формулам (292);
при этом в выражении для εа.с значение eа принимается со знаком
«минус». В настоящем пункте: yб, y'а - расстояние до рассматриваемого волокна соответственно от крайнего
сжатого волокна и центра тяжести арматуры A'; y0 -
то же, от центра тяжести приведенного сечения. Деформации ε0 в формулах настоящего пункта
со знаком «плюс» отвечают укорочению, а со знаком «минус» - удлинению. При одновременном действии
кратковременной и длительной нагрузок порядок вычисления ε0 аналогичен определению полной
кривизны согласно п. 4.20. 4.26. Укорочение (удлинение)
элементов на уровне рассматриваемого волокна определяется по формуле
где ε0i - относительные продольные деформации в сечении, расположенном
посередине участка длиной li; n -
число участков, на которые разбивается длина элемента. Приближенные методы
расчета деформаций
4.27. Прогибы железобетонных изгибаемых элементов постоянного сечения,
эксплуатируемых при влажности воздуха окружающей среды выше 40 %, заведомо
меньше предельно допустимых, если выполняется условие l/h0
≤ λгр, (297) где λгр - граничное отношение
пролета к рабочей высоте сечения, ниже которого проверки прогибов не требуется
(см. табл. 29). При l/h0 < 10 прогибы заведомо
меньше предельно допустимых, если выполняется условие (298), учитывающее влияние
поперечных сил на прогиб элемента, Табличные значения λгр отвечают длительному действию полной равномерно
распределенной нагрузки на свободно опертую балку при предельном прогибе,
равном l/200. Если предельно допустимые
прогибы (см. п. 1.19) меньше l/200 табличные значения λгр должны быть уменьшены в: Для сплошных плит толщиной
менее 25 см, армированных плоскими сетками, значения λгр уменьшаются путем деления на коэффициент, указанный
в п. 4.24. Примечание. Значения λгр могут быть увеличены в следующих случаях: а) если
прогиб определяется от действия момента Mдл, составляющего часть от полного момента Mп (поз. 2 - 4 табл. 2) -
путем умножения табличных значений λгр на отношение Mп/Mдл; б) если
нагрузка отличается от равномерно распределенной - путем умножения λгр на отношение в) если
прогиб определяется от совместного действия кратковременных, длительных и
постоянных нагрузок (поз. 1 и 5 табл. 2) - путем умножения λгр на коэффициент kθ, определяемый по формуле
где
θ - отношение деформации от длительного действия нагрузки к деформации от
кратковременного действия той же нагрузки, принимаемое равным: для элементов
прямоугольного сечения θ = 1,8; для элементов таврового сечения с полкой в
сжатой зоне θ = 1,5 и для элементов таврового сечения с полкой в растянутой
зоне θ = 2,2. Определение кривизны
4.28. Для изгибаемых элементов, указанных в п. 4.15 и эксплуатируемых при
влажности воздуха выше 40 %, когда нагрузки действуют только длительно или
только кратковременно, кривизна 1/ρ на участках с трещинами
определяется по формуле где k1, k2 - см. табл. 30. При одновременном действии
постоянных, длительных и кратковременных нагрузок (см. п. 1.13)
кривизна 1/ρ определяется по формуле где k1дл, k1кр, k2дл - коэффициенты k1 и k2, принимаемые по табл. 30
соответственно при кратковременном и длительном действии нагрузки. Определение
прогибов
4.29. Для элементов при l/h > 10 полный прогиб
принимается равным прогибу fM, обусловленному деформацией изгиба. Прогиб fM определяется следующим
образом: а) для элементов постоянного
сечения, работающих как свободно опертые или консольные балки, по формуле где 1/ρ0 - кривизна в
сечении с наибольшим изгибающим моментом от нагрузки, при которой определяется
прогиб; S - коэффициент, определяемый по табл. 31; б) для изгибаемых элементов с
защемленными опорами прогибы в середине пролета - по формуле где S - коэффициент, определяемый по табл. 31 как
для элементов с шарнирными опорами; Таблица 29
Таблица 30 в) если прогиб, определенный
по подпункту «а», превышает допустимый, то для слабоармированных изгибаемых
элементов (μ ≤ 0,5 %) его значение следует уточнить за счет
учета переменной по длине элемента жесткости, при этом наличие участков без
трещин по длине свободно опертых балок учитывается формулой где m - коэффициент, определенный по табл. 32 в зависимости от отношения Mт/Mп (Mт - см. пп. 4.3 и 4.4);
более точно величина f может быть найдена по
формуле (304)
за счет учета как участков без трещин, так и переменной жесткости на участках с
трещинами; г) для элементов переменного
сечения, а также в тех случаях, когда требуется более точное, чем по формулам (302) и
(303),
определение прогибов, а сами элементы и нагрузка симметричны относительно
середины пролета, величина f
определяется по формуле где Входящие в выражения (301)
- (304)
значения кривизн определяются по формулам (263), (281), (299), (300),
при наличии трещин в растянутой зоне и по формулам (261) и (262) -
при их отсутствии. Для сплошных плит толщиной
менее 25 см необходимо учитывать указания п. 4.24. 4.30. Для коротких элементов (l/h < 10) полный прогиб определяется по формуле В формуле (305): fM - прогиб, обусловленный
деформацией изгиба, вычисленный согласно п. 4.29; k - коэффициент, учитывающий влияние на прогиб
элемента поперечных сил и принимаемый равным: при отсутствии как
нормальных, так и наклонных трещин, т.е. при выполнении условий (221) и
(235): k
= 0,5/S; (306) при наличии нормальных или
наклонных трещин, а также одновременно и тех, и других: k = 1,5/S, (307) где S -
коэффициент, определяемый по табл. 31. Примеры
расчета
Пример
55. Дано:
железобетонная плита перекрытий гражданского здания прямоугольного сечения с
размерами h = 12 см; b = 100 см; h0 = 10,5 см; l = 3,1 м; бетон М 300 (Eб = 2,6·105 кгс/см2,
RрII = 15 кгс/см2); растянутая арматура класса
А-II (Eа =
2,1·106
кгс/см2) площадью поперечного сечения Fа = 3,93 см2 (5Æ10); полная равномерно распределенная нагрузка pполн = 700 кгс/м2, в
том числе ее часть от постоянных и длительных нагрузок pдл = 600 кгс/м2;
прогиб ограничивается эстетическими требованиями. Требуется рассчитать плиту по
деформациям. Расчет. Определяем необходимость
расчета плиты по деформациям согласно п. 4.27:
Из табл. 29 по μn = 0,03 и γ' = γ = 0 находим: λгр = 21. Так как h < 25 см, то λгр корректируем путем деления
на коэффициент
λгр = 21/1,23 = 17,4. Поскольку l/h0 = 310/10,5 = 29,6 больше λгрMп/Mдл = 17,4·0,84/0,72 = 20,3, расчет по деформациям необходим. Таблица 31
Таблица 32
Определяем кривизну в
середине пролета от действия момента Mдл (так как прогиб
ограничивается эстетическими соображениями). Принимаем без расчета, что
элемент имеет трещины в растянутой зоне, в связи с чем кривизну определяем по
формуле (299). По табл. 30
находим значения k1 = 0,39 и k2 = 0,10, соответствующие
длительному действию нагрузки.
Прогиб определяем согласно п.
4.29:
Так как h < 25 см, то полный прогиб
равен f = 1,42·1,23 = 1,72 см, что больше предельно допустимого прогиба l/200 = 310/200 = 1,55 см. Поскольку μ =
0,00375 < 0,005, то, согласно п. 4.29 «в», уточняем значение f по формуле (303).
Для этого вычисляем величины 1/ρс.у и Mт. Так как рассчитывается
слабоармированный элемент, то Mт и Iп определяем как для бетонного сечения Iп = bh3/12 = 100·123/12 = 14400 см4; Mт = 0,292bh2RрII = 0,292·100·122·15 = 63000 кгс·см;
Коэффициент m определяем при Mт/Mп = 0,630·105/(0,84·105)
= 0,76; по табл. 32 m =
0,086.
С учетом поправки на малую
высоту сечения (h < 25 см) f = 1,25·1,23 = 1,54 см, что
меньше предельно допустимого прогиба f =
1,55 см. Пример
56. Дано:
ригель перекрытия общественного здания, сечение прямоугольное с размерами b = 20 см; h = 60 см; a = 8 см; пролет ригеля l = 4,8 м; бетон марки М 300 (Eб = 2,6·105 кгс/см2,
RрII = 15 кгс/см2), рабочая арматура класса А-III (Eа = 2·106 кгс/см2);
площадь ее поперечного сечения Fа = 24,63 см2 (4Æ28); полная равномерно распределенная нагрузка pполн = 8,55 тс/м, в том числе ее
часть от постоянных и длительных нагрузок pдл = 6,4 тс/м; прогиб
ограничивается эстетическими соображениями; влажность воздуха в помещении выше
40 %. Требуется рассчитать ригель по
деформациям. Расчет. Определяем необходимость
расчета по деформациям согласно п. 4.27: h0 = 60 - 8 = 52 см;
Так как l/h = 4,8/0,6 = 8 < 10, то необходимо учитывать влияние поперечных сил
на прогиб элемента: l/h0 = 4,8/0,52 = 9,3. l/h0 + 18:l/h0 = 9,3
+ 18/9,3 = 11,24 > λгрMп/Mдл = 8·24,6/18,4
= 10,7, т.е. расчет по
деформациям необходим (λгр = 8 найдено по табл. 29 при μn = 0,182 и γ = γ' = 0). Поскольку μ =
0,0238 > 0,005, то, согласно п. 4.1, кривизну определяем с
учетом наличия трещин в растянутой зоне. Так как прогиб ограничивается
эстетическими требованиями, расчет ведем на действие момента Mдл. Кривизну в середине пролета 1/ρс вычисляем по формуле (299). По табл. 30 при μn = 0,182 и γ = γ' =
0 находим: k1 = 0,202 и k2 = 0;
Полный прогиб определяем,
согласно пп. 4.27
и 4.28,
с учетом влияния поперечных сил; согласно табл. 31, S = 5/48.
k =
1,5/S = 1,5·48/5 = 14,4;
т.е. прогиб ригеля меньше предельно допустимого (см.
табл. 2). Пример
57. Дано:
железобетонная плита покрытия с расчетным пролетом 5,7 м; размеры поперечного
сечения (для половины сечения плиты) по рис. 86; b = (9,5 + 6,5)/2 = 8 см; h = 30 см; h0 = 26,9 см; b'п = 73 см; h'п = 3 см; бетон М 300 (Eб = 2,6·105 кгс/см2; RрII = 170 мс/см2; RрII
= 15 кгс/см2); рабочая арматура класса А-II (Eа = 2,1·106 кгс/см2) площадью сечения Fа = 3,8 см2 (1Æ22); постоянная и длительная равномерно распределенная нагрузка на плиту
pдл = 875 кгс/м; прогиб плиты ограничивается
эстетическими соображениями; помещение, перекрываемое плитой, имеет влажность
воздуха ниже 40 %. Требуется рассчитать плиту по
деформациям. Расчет. Момент в середине плиты от
постоянных и длительных нагрузок для половины сечения равен
Поскольку определение
случаев, когда расчет прогибов можно не производить, а также приближенные
способы вычисления кривизны относятся к конструкциям, эксплуатируемым при
влажности воздуха окружающей среды выше 40 %, расчет кривизны производим по
формулам пп. 4.15 - 4.17 как для элементов с
трещинами в растянутой зоне ( Определяем кривизну плиты в
середине пролета по формуле (263). Заменяющий момент при действии внешнего
момента Mз = Mдл = 1,78 тс·м. Относительную
высоту сжатой зоны бетона ξ находим по формуле (264).
Для этого вычисляем величины: Рис. 86. Сборная
железобетонная плита покрытия
подставив которые в формулу (264), получим:
ξ = 0,163 > h'п/h0 = 3/26,9 =
0,112. Так как ξ
> h'п/h0, то продолжаем расчет как для таврового сечения.
Плечо внутренней пары сил z1 определяем по формуле (269):
Определяем коэффициент ψа согласно указаниям п. 4.17. Для этого находим по формуле
(233)
величину Wт:
Wт = (0,292 + 1,5μ1n + 0,075γ'1)bh2 = (0,292 + 1,5·0,128 + 0,075·1,63)8·302 =
4350 см3. Коэффициент m определяем по формуле (271),
учитывая, что для изгибаемого элемента Mяв =
M:
ψа = 1,25 - sm = 1,25 - 0,8·0,366 = 0,96. Кривизну плиты в середине
пролета определяем по формуле (263), принимая коэффициент v = 0,10.
Так как l/h = 570/30 = 19 > 10, то, согласно п. 4.29, прогиб f = fM, который определяем по формуле (301); согласно табл. 31, S = 5/48.
т.е. прогиб плиты меньше
предельно допустимого (см. табл. 2). 5. КОНСТРУКТИВНЫЕ
ТРЕБОВАНИЯ
ОБЩИЕ
УКАЗАНИЯ
5.1(5.1). При проектировании бетонных
и железобетонных конструкций и изделий для обеспечения условий их экономичного
и качественного изготовления, требуемой долговечности и совместной работы
арматуры и бетона надлежит выполнять конструктивные требования, изложенные в
настоящем разделе. 5.2. Конструкции должны
приниматься простого очертания. Следует использовать по возможности арматуру,
закладные детали и строповочные петли, выпускаемые в виде товарной продукции по
нормалям и ГОСТам. Арматуру следует проектировать в виде укрупненных блоков и
пространственных каркасов для сокращения времени укладки в форму (опалубку). Распалубочную и отпускную
прочность бетона следует назначать минимально возможными и для ускорения
оборота форм (опалубки) и интенсивного использования производственных площадей. Необходимо стремиться к
унификации арматуры и закладных деталей в отдельных конструкциях и их сериях,
небольшому числу разных марок и диаметров стали, типов арматурных элементов -
сеток и каркасов, шагов продольных и поперечных стержней. МИНИМАЛЬНЫЕ РАЗМЕРЫ
СЕЧЕНИЯ ЭЛЕМЕНТОВ
5.3(5.2). Размеры сечений бетонных и
железобетонных элементов, определяемые из расчета по действующим усилиям и
соответствующим предельным состояниям, должны назначаться с учетом
экономических требований, необходимости унификации форм и армирования, а также
условий принятой технологии изготовления конструкций. Кроме того, размеры
сечений железобетонных конструкций должны приниматься такими, чтобы соблюдались
требования в части расположения арматуры (толщины защитных слоев бетона,
расстояния между стержнями и т.п.) и анкеровки арматуры. 5.4(5.3).
Толщина* монолитных плит должна приниматься не
менее: для покрытий - 40 мм; для междуэтажных перекрытий
жилых и общественных зданий - 50 мм; для междуэтажных перекрытий
производственных зданий - 60 мм. Минимальная толщина сборных
плит должна приниматься из условий обеспечения требуемых толщин защитных слоев
бетона и расположения арматуры по толщине плиты (см. пп. 5.36 - 5.45). Размеры сечений
внецентренно-сжатых элементов должны приниматься такими, чтобы их гибкость l0/r в любом направлении, как правило, не превышала 200 (для прямоугольных
сечений l0/h
≤ 60), а для колонн,
являющихся элементами зданий, - 120 (l0/h
≤ 35). * Здесь
и далее величины, предписываемые и рекомендуемые настоящим Руководством
(размеры сечений, толщина защитного слоя бетона и др.), относятся к номинальным
значениям, назначаемым при проектировании и указываемым в чертежах. От этих
номинальных значений возможны отклонения в натуре, не превышающие величин,
указанных в соответствующих ГОСТах, технических условиях и др. ГАБАРИТЫ
И ОЧЕРТАНИЯ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ
5.5. Размеры сборных бетонных и железобетонных элементов следует назначать с
учетом грузоподъемных средств на заводе-изготовителе и на строительстве. В
необходимых случаях следует учитывать возможность подъема железобетонного изделия
вместе с формой. При назначении размеров
следует учитывать также условия перевозки: транспортные средства и допустимые
габариты. 5.6. Во избежание повреждений от
местных напряжений при резком изменении направлений граней изделия, например во
внутренних углах, рекомендуется предусматривать смягчение очертания в виде
уклонов, фасок или закруглений по возможности небольшой величины (до 50 мм),
чтобы не требовалось местное армирование (рис. 87,а, б, в). Рис. 87. Закругления и фаски а - ребристая плита, закругления; б - тавровая балка, фаска между полкой и стенкой; в - узел фермы, сочетание фаски и
закругления; г - смягчение острого угла в ригеле; д - отверстие в железобетонном
элементе для пропуска коммуникаций, строповки и т.д.; е - уклон при переходе от торца к
стенке балки (рекомендуется a:b ≥ 2) Во внешних углах во избежание
откалывания бетона при распалубке следует устраивать скосы или закругления
(рис. 87,г). 5.7. Отверстия в железобетонных
элементах для пропуска коммуникаций, строповки и т.п. следует принимать по
возможности небольшими и располагать их в пределах ячеек арматурных сеток и
каркасов так, чтобы не нужно было перерезать арматуру и вводить дополнительное
местное армирование. Углы отверстий желательно делать плавными (рис. 87,д). Обрамление отверстий
стальными закладными деталями замкнутой формы, особенно с острыми углами, не
рекомендуется во избежание образования трещин в бетоне вследствие его усадки. 5.8. При проектировании бетонных и железобетонных конструкций их очертание
следует принимать с учетом устройства и способа использования форм (опалубки). При применении форм с
откидными бортами очертание изделия не должно препятствовать повороту борта
(рис. 88,а)
при распалубке. При применении неразъемных
форм для возможности извлечения изделия из формы должны предусматриваться
уклоны не менее 1:10 (рис. 88,б, в).
В случае применения неразъемных форм с использованием выпрессовывания уклон
должен быть не менее 1:15 (рис. 88,г). При немедленной распалубке с
обеспечением фиксированного (во избежание нарушения бетона) вертикального
перемещения формующего элемента оснастки (рис. 88,д, е) уклон
должен быть не менее 1:50. При использовании форм с
одним неподвижным и одним откидным бортом для возможности вертикального подъема
конструкции при распалубке следует переход от большей ширины изделия к меньшей,
например от нижней полки к стенке (рис. 88,ж), принимать плавным
под углом не менее 40°. Это требование можно не предъявлять, если форма снабжена
выпрессовывающим устройством (рис. 88,з). Применение выпрессовывания и
немедленной распалубки должно согласовываться с изготовителем изделий. Рис. 88. Технологические
уклоны а -
в форме с откидными бортами; б, в - в неразъемной
форме; г - то же, с применением выпрессовщика; д, е - при немедленной
распалубке; ж - в форме
с глухим бортом; з - то же, с выпрессовщиком; 1 - изделие; 2
- форма; 3 - откидной борт; 4 -
выпрессовщик; 5 - вкладыш; 6 - формующая рамка АРМАТУРА, СЕТКИ И
КАРКАСЫ
Отдельные
арматурные стержни
5.9. Сортамент арматурных
стержней для железобетонных конструкций приведен в прил. 2. 5.10. При проектировании
железобетонных конструкций, в особенности с большим насыщением арматуры,
следует учитывать следующие характеристики арматурных стержней: фактические размеры
поперечных сечений стержней периодического профиля с учетом допускаемых
отклонений от них; радиусы загиба стержней и
соответствующие фактические габариты гнутых элементов; допускаемые отклонения от
проектных размеров при размещении стержней сварных сеток, каркасов, закладных
деталей и т.п. 5.11. При проектировании гнутых
стержней диаметры и углы загиба должны отвечать требованиям табл. 33. Таблица 33
Рис. 89. Размеры крюков на
концах стержней рабочей арматуры 5.12.
Размеры крюков для анкеровки гладких стержней
арматуры должны приниматься в соответствии с рис. 89. Сварные соединения
арматуры
5.13(5.32).
Арматура из горячекатаной стали периодического
профиля, горячекатаной гладкой стали и обыкновенной арматурной проволоки
должна, как правило, изготовляться с применением для соединений стержней
контактной сварки - точечной и стыковой, а также в указанных ниже случаях
дуговой (ванной и протяженными швами) сварки. Типы сварных соединений
арматуры должны назначаться и выполняться в соответствии с указаниями
государственных стандартов и нормативных документов (см. табл. 34). Соединения, не
предусмотренные государственными стандартами, допускается выполнять по рабочим
чертежам, утвержденным в установленном порядке. 5.14(5.33). Контактная точечная сварка применяется
при изготовлении сварных каркасов, сеток и закладных деталей с нахлесточными
соединениями стержней. 5.15(5.34). Контактная стыковая сварка
применяется для соединения по длине заготовок арматурных стержней. Диаметр
соединяемых стержней при этом должен быть не менее 10 мм. Контактную сварку стержней
диаметром менее 10 мм допускается применять только в заводских условиях при
наличии специального оборудования. 5.16.
Для соединения встык горизонтальных и
вертикальных стержней диаметром 20 мм и более при монтаже арматуры и сборных железобетонных конструкций рекомендуется предусматривать ванную
сварку в инвентарных съемных формах (поз. 3 табл. 34). Допускается в тех же
условиях применение ванной сварки, ванно-шовной сварки и сварки многослойными
швами с остающимися желобчатыми подкладками или накладками. 5.17. Проектирование сварных стыков
арматурных стержней с применением инвентарных форм и других формующих элементов
производится с учетом следующих требований: а) расстояния между
стыкуемыми стержнями, а также расстояния от стыкуемых стержней до ближайшей
грани железобетонного элемента должны назначаться с учетом возможности
установки формующих элементов и удаления инвентарных форм. Размеры и способы
установки инвентарных форм, желобчатых накладок, подкладок, а также расстояния
между стыкуемыми стержнями следует принимать согласно нормативным документам по
сварке. Расстояние от торцов стыкуемых выпусков до граней элементов (с учетом
защиты бетона от перегрева) - не менее 120 мм (рис. 90,а); б) расположение стыкуемых
стержней должно обеспечивать возможность ввода электрода под углом не более 30°
к вертикали (рис. 90,б, в); в) зазоры между стыкуемыми
стержнями при дуговой ванной сварке должны выполняться в соответствии с
требованиями государственных стандартов и нормативных документов по сварке. При
зазорах, превышающих максимально допустимые, соединение стержней допускается
производить с применением промежуточного элемента - вставки из арматурного
стержня того же диаметра и класса, что и стыкуемые стержни. При этом длина
вставки lb принимается
не менее 4d и не менее 150 мм (рис. 90,а). Рис. 90. Дуговая ванная сварка стержней а -
соединение при помощи вставки; б - горизонтальный стык; в - вертикальный стык Таблица 34 Основные типы сварных
соединений стержневой арматуры
5.18(5.35). Дуговая сварка протяженными швами должна применяться: а) для соединения стержней
арматуры из горячекатаных сталей диаметром более 8 мм между собой и с сортовым
прокатом (закладными деталями) в условиях монтажа, а также с анкерными и
закрепляющими устройствами; б) при изготовлении стальных
закладных деталей и для соединения их на монтаже между собой в стыках сборных
железобетонных конструкций. 5.19(5.36). При отсутствии оборудования для контактной сварки допускается применять
дуговую сварку в следующих случаях: а) для соединения по длине
заготовок арматурных стержней из горячекатаных сталей диаметром 8 мм и более; б) при выполнении сварных
соединений, рассчитываемых по прочности, в сетках и каркасах с обязательными
дополнительными конструктивными элементами в местах соединения стержней
продольной и поперечной арматуры (косынки, лапки, крюки и т.п.); в) при выполнении не
рассчитываемых по прочности крестовых соединений арматурных сеток из стержней
диаметром 8 мм и более. 5.20. Сварные стыки горячекатаной
арматуры рекомендуется располагать вразбежку или в зонах действия
незначительных моментов. Допускается стыкование стержней сваркой в любом
сечении по длине изделия. Стыки, осуществляемые дуговой сваркой, следует
располагать таким образом, чтобы они не препятствовали бетонированию, т.е.
устраивать их в местах, менее насыщенных арматурой, избегать устройства
нескольких стыков в одном сечении и т.п. Сварные сетки*
* Здесь и далее термином «сварные сетки»
обозначены плоские сварные арматурные изделия; термином «сварные каркасы» -
пространственные арматурные изделия. 5.21. При проектировании сеток
следует учитывать требования унификации габаритных размеров, шагов и диаметров
продольной и поперечной арматуры. Сетки должны быть удобны для
транспортирования, складирования и укладки в форму. Рекомендуется предусматривать
использование товарных сеток с параметрами по действующим стандартам, нормалям
и каталогам унифицированных изделий; арматурные сетки, не отвечающие этим
параметрам, следует проектировать с учетом изготовления их при помощи
контактной точечной сварки на многоэлектродных машинах. 5.22. Для изготовления сварных сеток с использованием контактной точечной
сварки следует применять арматуру классов А-I, А-II, А-III, В-I и Вр-I. Общие требования к
соотношению диаметров свариваемых стержней при контактной точечной сварке
приведены в табл. 35. 5.23. Сварка всех мест пересечений
стержней (узлов) является обязательной в сетках с нормируемой прочностью
крестообразных соединений. Допускается предусматривать сварку не всех мест пересечений стержней в сетках с
рабочей арматурой периодического профиля, применяемых для армирования плит, при
этом должны быть сварены все пересечения стержней в двух крайних рядах по
периметру сетки, остальные узлы могут быть сварены через узел в шахматном
порядке. 5.24. На концах стержней сварных
сеток, изготовляемых на многоэлектродных машинах, не должно быть крюков,
отгибов или петель. Таблица 35
5.25. При конструировании сварных сеток следует предусматривать возможность
их изготовления на многоэлектродных машинах. Справочные данные о параметрах
широких сварных сеток, изготовляемых на серийно выпускаемых многоэлектродных
машинах с помощью контактной точечной сварки, приводятся в табл. 36, а для узких сеток - в табл.
37. В целях сокращения числа
переналадок многоэлектродных машин рекомендуется при проектировании
унифицировать шаги арматуры, главным образом продольной, для железобетонных
изделий данной серии или каталога. Допускается принимать
отличающиеся от указанных в табл. 36 и 37 шаги стержней при разработке
чертежей железобетонных изделий для конкретного завода-изготовителя
применительно к параметрам установленного оборудования и при условии унификации
этих шагов на заводе. Сварные сетки, изготовляемые
на многоэлектродных машинах, должны иметь прямоугольный контур с прямоугольными
ячейками. При необходимости получения равнопрочного соединения стержни
периодического профиля (классов А-II и А-III) могут применяться только в одном направлении
(продольном или поперечном). 5.26. Сварные сетки,
конструктивные параметры которых не позволяют изготовлять их на
многоэлектродных машинах, допускается, в виде исключения, проектировать,
ориентируясь на технологические возможности одноточечных сварочных машин (табл.
38). 5.27. Товарные сварные сетки, а также сетки, изготовленные на
многоэлектродных и одноточечных машинах, могут быть использованы в виде
законченного арматурного изделия или как полуфабрикат, подвергаемый доработке
(разрезка сетки, вырезка отверстий, гнутье для получения пространственного
каркаса и в виде исключения - приварка дополнительных стержней). Таблица 36
Приварка дополнительных
стержней может производиться контактной сваркой с учетом требований табл. 35, 38 и
рис. 95,в, а также дуговой сваркой с учетом
требований п. 5.19
и рис. 91. Рис. 91. Образование сварной
сетки с приваркой дополнительного продольного стержня а -
исходная сетка; б - приварка
дополнительного стержня к основному вплотную электродуговой сваркой продольными
швами; в - приварка дополнительного стержня вблизи основного продольного
стержня при помощи точечной сварки; 1 - основной стержень; 2
- дополнительный; 3 - электродуговая сварка; d1 - диаметр дополнительного стержня Таблица 37
Таблица 38
Сгибание сетки производится в
соответствии с рекомендациями п. 5.31. 5.28. При армировании стенок балок
переменной высоты рекомендуется: а) при уклоне не более 1:10 -
применять сетки с группами стержней одной длины (рис. 92,а); б) при уклоне более 1:10 -
принимать раздельные прямоугольные сетки (рис. 92,б) или прямоугольные
сетки с последующей разрезкой по наклонной линии (рис. 92,в) с добавлением при необходимости окаймляющего стержня. 5.29. При армировании
непрямоугольных плит рекомендуется применять сварные сетки, получаемые из
прямоугольных в результате их разрезки (рис. 92,г). Рис. 92. Армирование изделий
переменных размеров а - армирование стенки балки переменной высоты сеткой с группами стержней
одной длины; б - то же, раздельными прямоугольными сетками; в -
то же, прямоугольной сеткой с разрезкой ее по наклонной линии и добавлением
окаймляющего стержня; г - сварная
сетка для армирования плиты переменной ширины, получаемая разрезкой
прямоугольной сетки Пространственные
арматурные каркасы
5.30. Арматуру железобетонных элементов
следует проектировать преимущественно, а линейных элементов - в особенности, в
виде пространственных каркасов. Пространственные каркасы
могут выполняться целиком на изделие либо в виде изготовленных заранее
пространственных блоков, применяемых в сочетании с плоскими или гнутыми
сетками, отдельными стержнями и т.п. Пространственные каркасы
следует конструировать достаточно жесткими для возможности их складирования,
перевозки и соблюдения проектного положения в форме. Пространственная жесткость
их должна обеспечиваться постановкой в необходимых случаях связей на сварке:
диагональных стержней, планок и т.п. Закладные детали и
строповочные устройства - петли, трубки и т.п. допускается заранее крепить к
пространственному каркасу. Если требуется высокая точность положения закладных
деталей, то фиксация должна осуществляться креплением их к форме. 5.31. При образовании пространственных каркасов с применением гнутья плоских
сеток рекомендуется предусматривать гнутые сетки с очертанием по типу
приведенных на рис. 93,а и получаемых на стандартном гибочном оборудовании. При этом
должны соблюдаться следующие требования: длина сеток - не более 6 м
(по согласованию с заводом-изготовителем допускается до 9 м); длина отгибаемого участка -
не менее 50 мм; углы загиба α - не
более 120°; диаметр изгибаемых стержней
из стали класса А-I - не более 12 мм, классов А-II и А-III - не более 10 мм, Вр-I и В-I - любой. При массовом изготовлении
допускаются гнутые сетки и других очертаний, например по типу приведенных на
рис. 93,б,
изготовление которых требует специального оборудования или приспособлений. Рис. 93. Примеры очертания гнутых сварных сеток а - рекомендуемые (изготовляются на стандартном оборудовании); б - допускаемые (требуют
нестандартного оборудования или приспособлений). Расположение прямых продольных
стержней показано условно Рис. 94. Параметры гнутых
сварных сеток а -
место загиба сетки удалено от продольных стержней, расположенных с внутренней
стороны; б - то же, с
наружной стороны; в -
место загиба сетки совпадает с продольным стержнем, расположенным с внутренней
стороны; для А-I, В-I D ≥ 4d, для А-III D ≥ 8d; г - то же, с наружной стороны; д - то же, при крупных диаметрах
продольных стержней; d -
диаметр гнутого стержня; D - внутренний диаметр загиба стержня; d1 - диаметр
продольного стержня Диаметры стержней гнутых
сварных сеток, радиусы и углы загиба, расположение продольных стержней следует
назначать с учетом классов применяемой стали в соответствии с указаниями,
приведенными на рис. 94. 5.32. Объединение арматурных изделий в пространственный каркас рекомендуется
предусматривать контактной точечной сваркой крестовых пересечений стержней при
помощи сварочных клещей. Минимальные расстояния в свету между стержнями, при
которых обеспечивается беспрепятственный проход электродов сварочных клещей для
каркасов железобетонных элементов, приведены на рис. 95. 5.33. Образование пространственных
каркасов для армирования линейных элементов типа колонн, свай, балок и т.п.
рекомендуется осуществлять следующими способами: плоские сетки соединяются
посредством отдельных стержней, привариваемых к продольным стержням сеток
контактной сваркой с помощью сварочных клещей (рис. 96,а), в соответствии с
п. 5.32
(при числе продольных стержней более четырех); пространственный каркас
образуется из гнутых сеток и соединительных стержней (рис. 96,б),
привариваемых как указано выше; пространственный каркас
образуется навивкой спиральной поперечной арматуры на продольную арматуру (рис.
96,в), причем в процессе навивки все
пересечения свариваются контактной точечной сваркой. Такие каркасы
рекомендуются для армирования труб, свай, бесконсольных колонн и других изделий
массового заводского изготовления; заранее согнутые и сваренные
контактной точечной сваркой в местах пересечения ветвей хомуты нанизываются на
продольные стержни с последующей контактной сваркой клещами всех пересечений
(рис. 96,г).
Места пересечения ветвей хомутов размещаются по длине каркаса вразбежку. Такие
каркасы могут применяться, в частности, для армирования колонн. При отсутствии
сварочных клещей может производиться вязка соединений продольных стержней и
хомутов (в этом случае рекомендуется обеспечивать пространственную жесткость
каркасов приваркой дополнительных стержней, планок и т.п.); плоская сетка гнется до
получения замкнутого контура, затем производится сварка клещами поперечных
стержней с продольным стержнем противоположного края исходной сетки (рис. 96,д).
Способ рекомендуется при наличии специального оборудования или
приспособлений; пространственный каркас
образуется путем сварки клещами четырех плоских сварных сеток по примеру,
показанному на рис. 96,е. Этот способ может быть применен, в частности, при
изготовлении каркасов колонн, когда расстояния между угловыми и средними
стержнями менее 75 мм, а число продольных стержней не менее 8.
Рис. 95. Примеры
пространственных каркасов железобетонных элементов, изготовляемых при помощи
сварочных клещей а - сварка стержней внешних углов каркасов линейных конструкций; б - сварка промежуточных стержней
каркасов линейных конструкций; в
- сварка стержней узкой сетки со стержнями двух широких сеток для
плоских конструкций; 1 - широкая сетка; 2
- узкая сетка; 3 - сварочные клещи для сварки
стержней обоих направлений диаметром до 16 мм Рис. 96. Примеры рекомендуемых
конструкций пространственных каркасов линейных элементов, собираемых с
применением контактной точечной сварки а -
из двух сеток и соединительных стержней, привариваемых к продольной арматуре
сеток; б - из гнутых
сеток и соединительных стержней; в
- с навивкой спиральной поперечной арматуры на продольную арматуру; г
- из заранее согнутых и сваренных хомутов, нанизанных на продольные стержни; д - из сетки, согнутой до получения
замкнутого контура; е - из
четырех плоских сеток; ж -
из двух сеток и монтажных стержней, перпендикулярных плоскости изгиба,
привариваемых к поперечной арматуре сеток (в балках, не работающих на кручение,
и в колоннах при общем насыщении продольной арматурой не более 3 %) 5.34. При отсутствии сварочных клещей образование пространственных каркасов
линейных элементов может быть выполнено следующими способами: плоские сетки соединяются при
помощи скоб из стержней класса А-I диаметром более 8 мм
посредством дуговой сварки их с хомутами (рис. 97,а). В колоннах, в
балках, работающих на кручение, а также в сжатой зоне балок с учитываемой в
расчете сжатой арматурой длина односторонних сварных швов l
должна быть не менее 6d (d - диаметр хомута), в монтажных соединениях - 3d; плоские сетки соединяются при
помощи шпилек с вязкой всех пересечений (рис. 97,б) и с обеспечением
монтажной жесткости каркаса приваркой стержней, планок и т.п.; плоские сетки соединяются
между собой путем дуговой сварки продольных стержней (рис. 97,в)
возле всех мест приварки хомутов. Длина швов l не менее 5d (d - диаметр хомута). Такие соединения допускаются при
насыщении сечения сжатой арматурой не более 3 %; вязаные пространственные
каркасы образуются из продольных стержней и гнутых хомутов с вязкой пересечений
и присоединением элементов жесткости (рис. 97,г). Из-за большой трудоемкости
каркасы, приведенные в п. 5.34, могут применяться лишь в виде исключения. Рис. 97. Примеры
пространственных каркасов линейных элементов, собираемых без применения
контактной точечной сварки а -
из двух плоских сеток и скоб, привариваемых к поперечной арматуре сеток; б
- из двух плоских сеток, соединяющихся при помощи шпилек с вязкой всех
пересечений; в - из
четырех плоских сеток; г -
из продольных стержней и гнутых хомутов с вязкой пересечений; 1 -
плоская сетка; 2 - скоба или шпилька 5.35. Образование пространственных каркасов для армирования плоских элементов
типа плит, стеновых панелей и т.п. рекомендуется производить следующим образом. Плоские каркасы типа
«лесенка» соединяются посредством соединительных стержней, привариваемых с
помощью сварочных клещей (рис. 98,а). Плоские сетки типа «лесенка»
одного направления соединяются при помощи таких же плоских сеток другого
направления и меньшей высоты (рис. 98,б). Соединения
пересечений осуществляются клещами; при их отсутствии допускается вязка. Пространственный каркас
ребристых или плоских элементов собирается из сеток «лесенка» по типу,
описанному выше, и дополняется одной или двумя плоскими сетками, привариваемыми
или привязываемыми к ним (рис. 98,в). Рис. 98. Примеры
рекомендуемых конструкций пространственных каркасов плоских элементов а -
из плоских сеток типа «лесенка» и соединительных стержней; б - из
плоских сеток типа «лесенка» одного направления и таких же сеток другого
направления и меньшей высоты; в
- то же, с добавлением одной или двух плоских сеток РАСПОЛОЖЕНИЕ АРМАТУРЫ,
АНКЕРОВКА, СТЫКИ
Защитный
слой бетона
5.36(5.4).
Защитный слой бетона для рабочей арматуры,
должен обеспечивать совместную работу арматуры с бетоном на всех стадиях работы
конструкции, а также защиту арматуры от атмосферных, температурных и т.п.
воздействий. 5.37.
Толщина защитного слоя должна составлять, как
правило, не менее диаметра стержня и не менее значений, указанных в табл. 39. Для сборных элементов из
бетона проектной марки М 250 и более толщину защитного слоя для продольной
арматуры допускается принимать на 5 мм меньше диаметра стержня, но не менее
величин, указанных в табл. 39. Для железобетонных плит и
балок из бетона марки М 250 и более, изготовляемых на заводах в металлических
формах и защищаемых в сооружении монолитным бетоном или стяжкой, толщину
защитного слоя для соответствующей арматуры допускается уменьшать на 5 мм. 5.38(5.10). В полых элементах
кольцевого или коробчатого сечения расстояния от стержневой продольной арматуры
до внутренней поверхности бетона должны удовлетворять требованиям п. 5.37. 5.39. Для растянутой продольной
рабочей арматуры, кроме арматуры фундаментов, толщину защитного слоя бетона в
пролете элемента следует принимать, как правило, не более 50 мм. В защитном слое
толщиной более 50 мм следует устанавливать конструктивную арматуру в виде
сеток; при этом площадь сечения продольной арматуры сеток должна быть не менее 0,1Fа, а шаг поперечной арматуры не
должен превышать высоты сечения элемента и требований п. 5.61. Таблица 39
5.40. Для конструкций, работающих
в агрессивных средах, толщина защитного слоя бетона должна назначаться с учетом
требований главы СНиП II-28-73 «Защита строительных
конструкций от коррозии». При назначении толщины
защитного слоя бетона должны также учитываться требования главы СНиП II-А.5-70 «Противопожарные нормы проектирования зданий
и сооружений». 5.41(5.9). Концы продольных рабочих
стержней арматуры, не привариваемых к анкерующим деталям, для удобства укладки
в форму или опалубку должны отстоять от торца элемента на расстоянии не менее: а) для сборных плит
перекрытий, стеновых панелей пролетом до 12 м и колонн длиной до 18 м - 10 мм; для сборных колонн длиной
более 18 м, опор и мачт любой длины - 15 мм; для прочих сборных элементов
длиной до 9 м - 10 мм; б) для монолитных элементов
длиной до 6 м при диаметре стержней арматуры до 40 мм - 15 мм; для монолитных элементов
длиной более 6 м при диаметре стержней до 40 мм и элементов любой длины при диаметре
стержней более 40 мм - 20 мм. При этом должна
обеспечиваться анкеровка стержней на опорах. Минимальные расстояния
между стержнями арматуры
5.42(5.11). Расстояния в свету между
стержнями арматуры по высоте и ширине сечения должны обеспечивать совместную
работу арматуры с бетоном и назначаться с учетом удобства укладки и уплотнения
бетонной смеси. При назначении расстояний
между стержнями в сварных сетках, каркасах следует, кроме того, учитывать
технологические требования по конструированию сварных арматурных изделий,
изложенные в пп. 5.25 - 5.35. 5.43(5.12). Расстояния в свету между отдельными стержнями продольной арматуры, а
также между продольными стержнями соседних сварных сеток и каркасов должны
приниматься не менее наибольшего диаметра стержней, а также: а) если стержни при
бетонировании занимают горизонтальное или наклонное положение - не менее: для
нижней арматуры - 25 мм и для верхней арматуры - 30 мм; при расположении нижней
арматуры более чем в два ряда по высоте расстояния между стержнями в
горизонтальном направлении (кроме стержней двух нижних рядов) должны
приниматься не менее 50 мм; б) если стержни при
бетонировании занимают вертикальное положение - не менее 50 мм; при
систематическом контроле фракционирования заполнителей бетона это расстояние
может быть уменьшено до 35 мм, но при этом должно быть не менее
полуторакратного наибольшего размера крупного заполнителя. В элементах или узлах с
большим насыщением арматурой или закладными деталями, изготовляемых без
применения виброплощадок или вибраторов, укрепленных на опалубке, должно быть
обеспечено в отдельных местах свободное расстояние в свету не менее 60 мм для
прохождения между арматурными стержнями наконечников глубинных вибраторов,
уплотняющих бетонную смесь. Расстояние между такими местами должно быть не
более 500 мм. 5.44(5.12). При стесненных условиях допускается располагать стержни арматуры
попарно (без зазора между ними) либо с расстоянием между парой стержней менее
расстояния, требуемого для отдельных стержней. Такая пара стержней при
назначении расстояний между стержнями по п. 5.43 при определении длины
анкеровки (по пп. 3.46, 5.47 - 5.50), а также при расчете по раскрытию трещин должна рассматриваться как
условный стержень диаметром: 5.45(5.12). Указанные в пп. 5.43 и 5.44 расстояния в свету между стержнями периодического профиля принимаются
по номинальному диаметру без учета выступов и ребер. При компоновке
расположения арматуры в сечении со стесненными условиями, с учетом примыкающих
других арматурных элементов и закладных деталей, следует принимать во внимание
диаметры стержней с учетом выступов и ребер, а также допускаемые отклонения от
номинальных размеров стержней, сварных сеток и каркасов, закладных деталей,
формы, расположения арматуры и закладных деталей в сечении. Рис. 99. Примеры расположения
одного из рядов стержней нижней арматуры (располагаемой в один или два ряда по
высоте) в случае изготовления изделия на виброплощадке а, б, в - варианты расположения стержней диаметром 32
мм; г, д, е - то
же, 16 мм; а, г -
одиночные расположения стержней; б,
д - спаренное расположение с уменьшенным расстоянием между парой
стержней; в, е - то
же, с расположением пар стержней вплотную. Пунктиром показаны условные стержни,
эквивалентные паре сближенных стержней Анкеровка
арматуры
5.46. При проектировании
железобетонных конструкций необходимо обеспечить надежную анкеровку арматуры в
бетоне, препятствующую их взаимному смещению. Анкеровка арматуры может
осуществляться одним из следующих способов или их сочетанием (рис. 100): сцеплением прямых стержней с
бетоном; крюками или лапками; петлями; приваркой поперечных
стержней; особыми приспособлениями
(анкерами). 5.47(5.13). Стержни периодического профиля, а также гладкие арматурные стержни,
применяемые в сварных каркасах и сетках, выполняются без крюков. Растянутые
гладкие стержни вязаных каркасов и вязаных сеток должны заканчиваться
полукруглыми крюками (рис. 89), лапками или петлями. 5.48(5.14). Продольные стержни растянутой и сжатой арматуры должны быть заведены за
нормальное к продольной оси элемента сечение, в
котором они учитываются с полным расчетным сопротивлением, на длину не менее lан, определяемую по формуле но не менее lан = λанd, где значения mан, ∆λан и λан, а также допускаемые
минимальные величины lан определяются по табл. 40. При
этом гладкие арматурные стержни должны оканчиваться крюками, выполняемыми
согласно п. 5.12,
или иметь приваренную поперечную арматуру по длине заделки. Рис. 100. Анкеровка арматуры а - сцеплением прямых стержней с бетоном; б - крюками и лапками; в - петлями; г - приваркой
поперечных стержней; д -
особыми приспособлениями (анкерами). Таблица 40(39)
Таблица 41
Величины относительной длины
анкеровки λан = lан/d, вычисленные по формуле (308)
для разных марок бетона и для разных классов арматуры, приведены в табл. 41. В случае когда анкеруемые
стержни поставлены с запасом по площади сечения против требуемой расчетом по
прочности, при определении lан по формуле (308)
значения Rа должны умножаться на величину, равную отношению
необходимой по расчету и фактической площади сечения арматуры. Если вдоль анкеруемых
стержней образуются трещины от растяжения бетона, то стержни должны быть
заделаны в сжатую зону бетона на длину lан, определяемую согласно
вышеуказанному. При этом высоту сжатой зоны допускается определять согласно п. 4.16. 5.49.
При невозможности выполнения требований п. 5.48 должны быть приняты
специальные меры по анкеровке продольных стержней: а) устройство на концах
стержней специальных анкеров в виде пластин, гаек, уголков, высаженных головок
и т.п. (рис. 101).
В этом случае площадь контакта анкера с бетоном из условия прочности бетона на
смятие должна быть не менее: б) отгиб анкеруемого стержня
на 90° по дуге круга (рис. 102); на отогнутом участке ставятся
дополнительные хомуты против разгибания стержней; в) приварка на длине заделки
не менее двух поперечных анкерующих стержней диаметром не менее 0,5 диаметра
продольных стержней; в этом случае длина анкеровки lан, определенная, согласно п. 5.48, для стержней
периодического профиля, уменьшается на 5d, а гладкие стержни выполняются без крюков (рис. 103,а). Рис. 101. Анкеровка арматуры
путем устройства на концах специальных анкеров а - приваренная пластина; б - обжатая пластина; в - высаженная головка; г - высаженная головка с шайбой; д - приварка стержней к уголку; е - гайка с шайбой снаружи; ж - гайка внутри Рис. 102. Анкеровка арматуры
путем ее загибания 1 - дополнительные хомуты, препятствующие разгибанию стержня Рис. 103. Дополнительная
анкеровка арматуры путем приварки поперечных анкерующих стержней а - плит; б - балок 5.50(5.15). Для обеспечения анкеровки всех продольных стержней арматуры, доходящих
до опоры, на крайних свободных опорах изгибаемых элементов должны выполняться
следующие требования: а) если соблюдается условие (47) п. 3.31,
длина запуска растянутых стержней за внутреннюю грань свободной опоры lа должна составлять не менее 5d. В сварных сетках и каркасах с
продольной рабочей арматурой из гладких стержней к каждому растянутому
продольному стержню на длине lа должен быть приварен хотя бы
один поперечный (анкерный) стержень, расположенный от конца каркаса (сетки) на
расстоянии l ≥ 15 мм при d ≤ 10 мм и c
≥ 1,5d при d > 10 мм (рис. 103,а). Диаметр анкерующего стержня dа в балках и ребрах должен
быть не менее половины диаметра продольных стержней; б) если условие (47) не
соблюдается, длина запуска стержней за внутреннюю грань свободной опоры lа должна быть не менее 10d. В случае применения гладких стержней на длине lа к каждому продольному
стержню должно быть приварено не менее двух поперечных (анкерующих) стержней
диаметром dа ≥ 0,5d; при этом расстояние от
крайнего анкерующего стержня до конца сетки или каркаса должно быть не более
указанных выше величин c (рис. 103,б). Длина запуска стержней за
внутреннюю грань опоры уменьшается против требуемой настоящим пунктом, если
величина lан < 10d, и принимается равной lан, но не менее 5d. Стыки арматуры
внахлестку (без сварки)
5.51(5.37). Стыки рабочей арматуры
внахлестку применяются при стыковании как сварных, так и вязаных каркасов и
сеток. При этом диаметр рабочей арматуры должен быть не более 36 мм. Стыки стержней рабочей арматуры
внахлестку не рекомендуется располагать в растянутой зоне изгибаемых и
внецентренно-растянутых элементов в местах полного использования арматуры.
Такие стыки не допускаются в линейных элементах, сечение которых полностью
растянуто. 5.52(5.38). Стыки растянутой или сжатой рабочей арматуры, а также сварных сеток и
каркасов в рабочем направлении должны иметь длину перепуска (нахлестки) lн не менее
величины, определяемой по формуле где σа
- напряжение в арматуре в месте стыка внахлестку с наиболее напряженной стороны
(рис. 104). Рис. 104. Длина перепуска
(нахлестки) арматуры в стыках Значения mн и ∆λн,
а также минимальные значения lн и λн для определения длины
перепуска стыков арматуры внахлестку приведены в табл. 42. В случае спаренного
расположения стержней длина нахлестки устанавливается по приведенной выше
формуле (309),
принимая значение d =
dпр, определенное согласно п. 5.44. Относительная длина перепуска
λн = lн/d в зависимости от прочности бетона и напряжений в арматуре приведена в
табл. 43. Таблица 42(39)
5.53(5.39). Стыки сварных сеток и
каркасов, а также растянутых стержней вязаных каркасов и сеток внахлестку без
сварки должны, как правило, располагаться вразбежку. При этом площадь сечения
рабочих стержней, стыкуемых в одном месте или на расстоянии менее длины
перепуска lн, должна составлять не более
50 % общей площади сечения растянутой арматуры при стержнях периодического
профиля и не более 25 % при гладких стержнях. Смещение стыков,
расположенных в разных местах, должно быть не менее 1,5lн (рис. 105,б).
Стыкование отдельных стержней, сварных сеток и каркасов без разбежки
допускается при конструктивном армировании (без расчета), а также на тех
участках, где арматура используется не более чем на 50 %. В поперечном сечении элемента
арматурные стыки следует располагать по возможности симметрично. 5.54. При стыке внахлестку
стыкуемые стержни должны располагаться по возможности вплотную друг к другу; расстояние в свету между
стыкуемыми стержнями не должно превышать 4d, т.е. 0 ≤ e ≤ 4d (рис. 105,а). Соседние стыки внахлестку не
должны располагаться слишком близко друг к другу. Расстояние между ними в свету
должно быть не меньше 2d (d - диаметр стыкуемых стержней)
и не меньше 30 мм (рис. 105,б). 5.55(5.40). Стыки сварных сеток в
рабочем направлении можно выполнять внахлестку с расположением
распределительных стержней в одной или в разных плоскостях. Таблица 43
В каждой из стыкуемых в
растянутой зоне сварных сеток с рабочими стержнями из гладкой стали на длине
нахлестки должно быть не менее двух поперечных стержней, приваренных ко всем
продольным стержням сетки (рис. 106). Диаметр поперечных анкерующих
стержней должен быть не менее одной трети диаметра продольного анкеруемого
стержня и не менее величин, указанных в п. 5.22. Длина нахлестки сварных сеток
с гладкой рабочей арматурой при наличии двух приваренных анкерующих стержней по
длине нахлестки должна быть не менее величины lн, определенной по указаниям
п. 5.52. Такие же типы стыков
применяются и для стыкования внахлестку сварных сеток и каркасов с односторонним
расположением рабочих стержней из всех видов стали. Стыки сварных сеток в
направлении рабочей арматуры периодического профиля классов А-II и А-III выполняются без поперечных
стержней в пределах стыка в одной или в обеих стыкуемых сетках (рис. 107,а,
б), при этом длина нахлестки принимается в соответствии с требованиями
п. 5.52. При приварке поперечных
анкерующих стержней к рабочим стержням периодического профиля сварных сеток и
каркасов длина нахлестки, определенная по указаниям п. 5.52, может быть уменьшена: на 5d - при одном поперечном
анкерующем стержне; на 8d - при двух поперечных анкерующих стержнях. Во всех случаях длина
нахлестки должна быть не менее 15d в
растянутом и 10d - в сжатом бетоне. Если диаметр рабочих
стержней, стыкуемых внахлестку в растянутой зоне, превышает 10 мм и расстояния
между стержнями составляют менее величины
(Fа - площадь сечения всех стыкуемых продольных
стержней). При стыковании внахлестку
сварных и вязаных каркасов в балках на длине стыка независимо от диаметра
рабочих стержней должна ставиться дополнительная поперечная арматура в виде
хомутов или корытообразно согнутых сварных сеток; при этом шаг дополнительных
поперечных стержней в пределах стыка должен быть не более 5d (d - наименьший диаметр продольных рабочих стержней). При стыковании внахлестку
сварных (и вязаных) каркасов центрально- и внецентренно-сжатых колонн в
пределах стыка должны ставиться дополнительные хомуты на расстояниях не более
10d. 5.56(5.41). Стыки сварных сеток в
нерабочем направлении выполняются внахлестку с перепуском, считая между осями
крайних рабочих стержней сетки: а) при диаметре
распределительной арматуры до 4 мм включительно - на 50 мм (рис. 108,а,
б); Рис. 105. Расположение стержней,
стыкуемых внахлестку а - расположение в стыке стержней периодического профиля и гладких; б
- расположение стыков Рис. 106. Стыки внахлестку
(без сварки) сварных сеток в направлении рабочей арматуры из гладких стержней а -
с расположением распределительных стержней в одной плоскости; б, в - с расположением распределительных стержней в разных плоскостях Рис. 107. Стыки внахлестку
(без сварки) сварных сеток в направлении рабочей арматуры периодического
профиля а - без анкерующих поперечных стержней на двух сетках; б - без анкерующих стержней на одной
из сеток; в - при одном анкерующем
стержне; г - при двух
анкерующих стержнях Рис. 108. Стыки внахлестку
(без сварки) сварных сеток в направлении распределительной арматуры а, б - при диаметре распределительной арматуры до 4 мм включительно; в, г - при диаметре
распределительной арматуры более 4 мм; д - при диаметре рабочей арматуры 16 мм и более б) при диаметре
распределительной арматуры более 4 мм - на 100 мм (рис. 108,в, г). При диаметре рабочей арматуры
16 мм и более сварные сетки в нерабочем направлении допускается укладывать
впритык друг к другу, перекрывая стык специальными стыковыми сетками,
укладываемыми с перепуском в каждую сторону не менее 15 диаметров
распределительной арматуры и не менее 100 мм (рис. 108,д). Сварные сетки в нерабочем
направлении допускается укладывать впритык без нахлестки и без дополнительных
стыковых сеток в следующих случаях: в) при укладке сварных
полосовых сеток в двух взаимно перпендикулярных направлениях; г) при наличии в местах стыков
дополнительного конструктивного армирования в направлении распределительной
арматуры. АРМИРОВАНИЕ
ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ
Общие
требования
5.57(5.16). Площадь сечения продольной
арматуры в железобетонных элементах (в процентах от площади расчетного сечения
бетона) должна приниматься не менее указанной в табл. 44. Таблица 44(40)
Требования настоящего пункта не учитываются
при назначении площади сечения арматуры, устанавливаемой по контуру плит или
панелей из расчета на изгиб в плоскости плиты (панели). Минимальное армирование
стеновых панелей принимается в соответствии с инструкцией по проектированию
панельных жилых зданий. 5.58(5.22). У всех поверхностей железобетонных элементов, вблизи которых ставится
продольная арматура, должна предусматриваться также поперечная арматура,
охватывающая крайние продольные стержни. При этом расстояния между поперечными
стержнями у каждой поверхности элемента должны быть не более 500 мм и не более
удвоенной ширины грани элемента. Поперечную арматуру можно не ставить у граней
тонких ребер изгибаемых элементов (шириной 150 мм и менее), по ширине которых
располагается лишь один продольный стержень, каркас или одна сетка. 5.59. Соответствие расположения
арматуры ее проектному положению должно обеспечиваться специальными
мероприятиями по фиксации арматуры согласно пп. 5.121 - 5.124. Армирование сжатых
элементов
Продольная арматура
5.60(5.17). Диаметр продольных стержней
сжатых элементов не должен превышать для бетона марок ниже М 300 - 40 мм. Для особо мощных колонн при
марке бетона выше М 200 и соответствующем технологическом обеспечении (резка,
сварка и т.п.) могут применяться стержни диаметром более 40 мм. В колоннах с размером меньшей
стороны сечения 250 мм и более диаметр продольных стержней рекомендуется
назначать не менее 16 мм. Диаметр продольных стержней
внецентренно-сжатых элементов монолитных конструкций должен быть не менее 12
мм. 5.61(5.18). В линейных внецентренно-сжатых элементах расстояние между осями стержней
продольной арматуры должно приниматься не более 400 мм. При расстоянии между рабочими
стержнями более 400 мм надлежит ставить конструктивную арматуру диаметром не
менее 12 мм с тем, чтобы расстояния между продольными стержнями были не более
400 мм. 5.62(5.19). Во внецентренно-сжатых
элементах, несущая способность которых при заданном эксцентрицитете продольной
силы используется менее чем на 50 %, а также в элементах с гибкостью l0/r < 17 (например, подколонники), где по расчету сжатая
арматура не требуется, а число растянутой арматуры не превышает 0,3 %,
допускается не устанавливать продольную и поперечную арматуру, требуемую,
согласно пп. 5.58,
5.61,
5.63
и 5.64,
по граням, параллельным плоскости изгиба. При этом армирование по граням,
перпендикулярным к плоскости изгиба, производится сварными каркасами и сетками
с толщиной защитного слоя бетона не менее 50 мм и не менее двух диаметров
продольной арматуры. Поперечная
арматура
5.63(5.22). Конструкция поперечной арматуры должна обеспечивать закрепление сжатых
стержней от их бокового выпучивания в любом направлении. Во внецентренно-сжатых
линейных элементах при наличии учитываемой в расчете сжатой продольной арматуры
хомуты должны ставиться на расстояниях не более 500 мм и при вязаных каркасах
не более 15d, а при сварных - не более 20d (d - наименьший диаметр сжатых продольных стержней). Расстояния между хомутами
внецентренно-сжатых элементов в местах стыкования рабочей арматуры внахлестку
без сварки должны составлять не более 10d. Если общее насыщение элемента
продольной арматурой составляет более 3 %, хомуты должны устанавливаться на
расстояниях не более 10d и не более 300 мм. При проверке соблюдения
требований настоящего пункта продольные сжатые стержни, не учитываемые
расчетом, не должны приниматься во внимание, если диаметр этих стержней не
превышает 12 мм и не более половины толщины защитного слоя бетона. 5.64(5.23). При армировании внецентренно-сжатых элементов плоскими сварными
каркасами два крайних каркаса (расположенных у противоположных граней) должны
быть соединены друг с другом для образования пространственного каркаса. Для
этого у граней элемента, нормальных к плоскости каркасов, должны ставиться
поперечные стержни, привариваемые контактной точечной сваркой к угловым
продольным стержням каркасов, или шпильки, связывающие эти стержни, на тех же
расстояниях, что и поперечные стержни плоских каркасов. Если крайние плоские каркасы
имеют промежуточные продольные стержни, то последние, по крайней мере, через
один и не реже чем через 400 мм по ширине грани элемента должны связываться с
продольными стержнями, расположенными у противоположной грани, при помощи
шпилек. Шпильки допускается не ставить при ширине данной грани элемента не
более 500 мм, если число продольных стержней у этой грани не превышает четырех. При больших размерах сечения
элемента рекомендуется установка промежуточных плоских сварных каркасов (рис. 109,а). Конструкция вязаных хомутов
во внецентренно-сжатых элементах должна быть такова, чтобы продольные стержни
(по крайней мере через один) располагались в местах перегиба хомутов, а эти
перегибы - на расстоянии не более 400 мм по ширине грани элемента. При ширине
грани не более 400 мм и числе продольных стержней у этой грани не более четырех
допускается охват всех продольных стержней одним хомутом (рис. 109,б).
На концах вязаных хомутов должны предусматриваться крюки. Рис. 109. Конструкция
пространственных каркасов в центрально- и внецентренно-сжатых элементах а -
армирование сварными каркасами; б
- армирование вязаными каркасами; 1 - плоские сварные каркасы; 2
- соединительные стержни; 3 - вязаный хомут; 4
- промежуточный плоский сварной каркас; 5 - шпилька 5.65(5.25). Диаметр хомутов в вязаных
каркасах внецентренно-сжатых линейных элементов должен приниматься не менее
0,25d и не менее 5 мм, где d - наибольший диаметр продольных стержней. Соотношение диаметров
поперечных и продольных стержней в сварных каркасах и сетках устанавливается из
условия сварки согласно п. 5.22. Армирование изгибаемых
элементов
Продольная арматура
5.66(5.20). Балки и ребра шириной 150 мм
и менее (рис. 110),
работающие в основном на изгиб, могут армироваться одной плоской вертикальной
сеткой, а шириной более 150 мм и при значительных нагрузках - должны
армироваться несколькими вертикальными сетками (каркасами). В балках шириной более 150 мм
число продольных рабочих стержней, доводимых до опоры, должно быть не менее
двух. В ребрах сборных панелей, настилов, часторебристых перекрытий и т.п.
шириной 150 мм и менее допускается доведение до опоры одного продольного
рабочего стержня (рис. 110). Рис. 110. Армирование балок
плоскими сварными каркасами 1 - соединительные стержни; 2 - плоские сварные каркасы 5.67(5.21). В изгибаемых элементах при
высоте сечения более 700 мм у боковых граней должны ставиться конструктивные
продольные стержни с расстояниями между ними по высоте не более 400 мм и с
площадью сечения не менее 0,1 % площади сечения бетона, с размерами, равными:
по высоте элемента - расстоянию между этими стержнями, по ширине элемента -
половине ширины ребра элемента, но не более 200 мм (рис. 111). Рис. 111. Установка
конструктивной продольной арматуры по высоте сечения балки 1 - конструктивные продольные стержни 5.68(5.20). В плитах расстояния между
рабочими стержнями, доводимыми до опоры, не должны превышать 400 мм, причем
площадь сечения этих стержней на 1 м ширины плиты должна составлять не менее 1/3
площади сечения стержней в пролете, определенной расчетом по наибольшему
изгибающему моменту. Расстояние между осями
рабочих стержней в средней части пролета плиты и над опорой (вверху) должно быть
не более 200 мм при толщине плиты до 150 мм и не более 1,5h - при толщине плиты более
150 мм (h - толщина плиты). При армировании неразрезных
плит сварными рулонными сетками допускается вблизи промежуточных опор все
нижние стержни отгибать в верхнюю зону. Расстояние между стержнями
распределительной арматуры балочных плит должно быть не более 500 мм. Примечания: 1. В многопустотных настилах расстояние между осями рабочих стержней
разрешается увеличивать в соответствии с расположением пустот в сечении, но не
более чем до 2h. 2. В
плитах толщиной более 350 мм расстояние между осями рабочих стержней диаметром
более 20 мм разрешается увеличивать до 600 мм. 3. При армировании сварными сетками сплошных
балочных плит толщиной 120 мм и более и при содержании растянутой рабочей
арматуры до 1,5 % расстояние между стержнями распределительной арматуры
допускается увеличивать до 600 мм. 5.69. Если рабочая арматура плиты
проходит параллельно ребру, необходимо укладывать перпендикулярно к нему
дополнительную арматуру сечением не менее 1/3 наибольшего
сечения рабочей арматуры плиты в пролете, заводя ее в плиту в каждую сторону от
грани ребра на длину не менее 1/4 расчетного пролета
плиты. Если рабочая арматура плиты
над опорой проходит перпендикулярно к ребру, следует обрывать ее не ближе чем
на расстоянии 1/4 расчетного пролета плиты от грани ребра
(рис. 112). Площадь сечения
распределительной арматуры в балочных плитах должна составлять не менее 10 %
площади сечения рабочей арматуры в месте наибольшего изгибающего момента. Рис. 112. Армирование
приопорных участков плит, монолитно связанных с балками 1 - рабочая арматура плиты; 2 - рабочая
надопорная арматура плиты; l - расчетный пролет плиты Поперечная и отогнутая арматура
5.70(5.26). В балках и ребрах высотой более 150 мм, а также в многопустотных
сборных плитах (или аналогичных часторебристых конструкциях) высотой более 300
мм должна устанавливаться вертикальная поперечная арматура. В сплошных плитах, а также в
балках и ребрах высотой 150 мм и менее и в многопустотных сборных плитах (или
аналогичных часторебристых конструкциях) высотой 300 мм и менее допускается
поперечную арматуру не устанавливать. При этом должны быть обеспечены
требования расчета согласно пп. 3.42 и 3.43. 5.71. В сжатой зоне изгибаемых
элементов при наличии учитываемой в расчете сжатой продольной арматуры должны
устанавливаться поперечные стержни (хомуты) на расстояниях, указанных в п. 5.63. 5.72(5.25). Диаметр хомутов в вязаных каркасах изгибаемых элементов должен
приниматься не менее: при h ≤ 800 мм - 6 мм; при h > 600 мм - 8 мм. Соотношение диаметров
поперечных и продольных стержней в сварных каркасах и сварных сетках,
устанавливаемое из условия сварки, принимается согласно п. 5.22. 5.73(5.27). Расстояние между вертикальными поперечными стержнями в элементах, не
имеющих отогнутой арматуры, в случаях, когда поперечная арматура требуется по
расчету либо по конструктивным соображениям, указанным в п. 5.70, должно приниматься: а) на приопорных участках
(равных при равномерной нагрузке 1/4 пролета, а при
сосредоточенных нагрузках - расстоянию от опоры до ближайшего груза, но не
менее 1/4 пролета): при высоте сечения h ≤ 450 мм - не более h/2 и не более 150 мм; при высоте сечения h > 450 мм - не более h/3 и не более 500 мм; б) на остальной части пролета
при высоте сечения h
> 300 мм - не более 3/4h и не
более 500 мм. 5.74. Для обеспечения анкеровки поперечной арматуры изгибаемых элементов
соединения продольных и поперечных стержней в сварных каркасах должны быть
выполнены в соответствии с требованиями пп. 5.13, 5.22 - 5.27; в вязаных каркасах хомуты
должны конструироваться таким образом, чтобы в местах их перегиба, а также
загиба концевых крюков (при отсутствии перепуска концов) обязательно
располагались продольные стержни (рис. 113). При этом как в сварных,
так и в вязаных каркасах диаметр продольных стержней должен быть не менее
диаметра поперечных. При вязаной арматуре в
промежуточных (средних) балках таврового сечения, монолитно соединенных поверху
с плитой, рекомендуется ставить открытые хомуты. Рис. 113. Конструкция хомутов
вязаных каркасов балок Рис. 114. Конструкция отгибов
арматуры Рис. 115. Положения отгибов,
определяемые эпюрой изгибающих моментов в балке 1 - начало отгиба в растянутой зоне А; 2 - то же, в зоне Б; 3 - сечение, в котором стержень «а» не
требуется по расчету зоны А; 4 - сечение, в котором стержень «б» не
требуется по расчету зоны Б; 5
- эпюра моментов; 6 - эпюра материалов Рис. 116. «Плавающий»
стержень 5.75(5.29). Отогнутые стержни арматуры должны предусматриваться в изгибаемых
элементах при армировании их вязаными каркасами и в коротких консолях. Отгибы
стержней должны осуществляться по дуге радиуса не менее 10d (рис. 114). В изгибаемых элементах на концах отогнутых стержней должны
устраиваться прямые участки длиной не менее 0,8lан, принимаемой согласно
указаниям п. 5.48, но не менее 20d в растянутой и 10d в сжатой зоне. Прямые участки отогнутых
гладких стержней должны заканчиваться крюками. Начало отгиба в растянутой
зоне должно отстоять от нормального сечения, в котором отгибаемый стержень
используется по расчету, не менее чем на 0,5h0, а конец отгиба должен быть расположен не ближе того
нормального сечения, в котором отгиб не требуется по расчету (рис. 115). Расстояние от грани свободной
опоры до верхнего конца первого отгиба (считая от опоры) должно быть не более
50 мм. 5.76. Угол наклона отгибов к
продольной оси элемента следует, как правило, принимать равным 45°. В балках
высотой более 800 мм и в балках-стенках допускается увеличивать угол наклона
отгибов в пределах до 60°, а в низких балках и в плитах уменьшать его в
пределах до 30°. Стержни с отгибами
рекомендуется располагать на расстоянии не менее 2d от боковых граней элемента, где d -
диаметр отгибаемого стержня. Отгибать стержни, расположенные непосредственно у
боковых граней элементов, не рекомендуется. Отгибы стержней рекомендуется
располагать симметрично относительно продольной оси балки. Применение отгибов в виде
«плавающих» стержней (рис. 116) не допускается. Армирование элементов,
работающих на изгиб с кручением
5.77(5.31). В элементах, работающих на
изгиб с кручением, вязаные хомуты должны быть замкнутыми с перепуском их концов
на 30d, где d - диаметр хомута, а при
сварных каркасах все поперечные стержни обоих направлений должны быть приварены
к угловым продольным стержням, образуя замкнутый контур (рис. 117). Пространственные каркасы
следует проектировать с учетом требований пп. 5.31 - 5.34. Расстояния между поперечными
стержнями, расположенными у граней, нормальных к плоскости изгиба, должны
составлять не более ширины сечения элемента b; у граней, сжатых от изгиба,
при Mк ≤ 0,2M допускается увеличивать расстояния между поперечными
стержнями, принимая их в соответствии с пп. 5.58 и 5.63. Рис. 117. Армирование балок,
работающих на кручение а - вязаной арматурой; б - сварным каркасом Требования настоящего пункта
относятся, в частности, к крайним балкам, к которым второстепенные балки или
плиты примыкают лишь с одной стороны (обвязочные балки, балки у температурных
швов и т.п.), а также к средним балкам, для которых расчетные нагрузки,
передающиеся на балку от примыкающих к ней пролетов, различны и отличаются друг
от друга более чем в 2 раза. ОСОБЫЕ СЛУЧАИ
АРМИРОВАНИЯ
Армирование
в местах отверстий
5.78(5.50). Отверстия значительных
размеров в железобетонных плитах, панелях и т.п. должны окаймляться
дополнительной арматурой сечением не меньше сечения рабочей арматуры (того же
направления), которая требуется по расчету плиты как сплошной. Дополнительная
арматура должна быть заведена за края отверстия на длину не менее длины
перепуска lн, указанной в табл. 43. Отверстия в стенках элементов
должны иметь закругленную форму и усиливаться по краям арматурой. Армирование плит в
зоне продавливания
5.79(5.28). Поперечная арматура, устанавливаемая в плитах в зоне продавливания,
должна иметь анкеровку по концам, выполняемую приваркой или охватом продольной
арматуры. Расстояние между поперечными стержнями принимается не более 1/3h и не более 200 мм, где h - толщина плиты. Ширина зоны
постановки поперечной арматуры должна быть не менее 1,5h. Конструирование
коротких консолей
5.80. Короткие консоли могут быть
постоянной высоты h или переменной с увеличением
к месту заделки (рис. 118). Консоли переменной высоты
следует предусматривать при больших нагрузках. 5.81(5.30). Поперечное армирование коротких консолей рекомендуется выполнять
следующим образом: при h ≤ 2,5a - консоль армируется наклонными
хомутами по всей высоте (рис. 118,б); при h > 2,5a - консоль армируется
отогнутыми стержнями и горизонтальными хомутами по всей высоте (рис. 118,в); при h > 3,5a и Q ≤ Rрbh0 - отогнутые стержни
допускается не устанавливать; здесь h0 принимается в опорном сечении
консоли. Во всех случаях шаг хомутов
должен быть не более h/4 и
не более 150 мм. Диаметр отогнутых стержней должен быть не более 1/15
длины отгиба lот и не более 25 мм (рис. 118,в). Суммарная площадь сечения
отогнутых стержней, наклонных хомутов, пересекающих верхнюю половину линии
длиной l, соединяющей точки
приложения силы Q и сопряжения нижней грани
консоли и колонны (рис. 118,б и в), должна
быть не менее 0,002bh0. При ограниченной высоте
консоли допускается применение жесткой арматуры (рис. 118,а). Рис. 118. Конструирование
коротких консолей а - прямоугольная консоль с жесткой арматурой; б - консоль
переменной высоты с наклонными хомутами; в - консоль переменной высоты с
отогнутыми стержнями и горизонтальными хомутами Косвенное
армирование
5.82(5.24). Косвенное армирование препятствует поперечному расширению бетона,
благодаря чему увеличивается прочность бетона при продольном сжатии. Косвенное армирование применяется
в виде спиралей или колец (рис. 119) или в виде пакета поперечных сварных сеток
(рис. 120). Для косвенного армирование
следует применять арматурную сталь классов А-I, А-II, А-III, В-I и Вр-I диаметром не более 14 мм,
преимущественно 5 - 10 мм. Предпочтительно применять
косвенную арматуру из более прочной стали. Косвенное армирование может
применяться по всей длине сжатых элементов (колонн, свай) или в качестве
местного косвенного армирования в местах стыков колонн, в местах воздействия
ударов на сваю и др. Кроме того, косвенное армирование в виде сеток применяется
при местном сжатии (смятии). В колоннах и сваях сетки и
спирали (кольца) должны охватывать всю рабочую продольную арматуру. 5.83(5.24). При применении косвенного
армирования в виде спирали или колец должны соблюдаться следующие условия (рис.
119): спирали и кольца в плане
должны быть круглыми; расстояние между витками
спирали или кольцами в осях должно быть не менее 40 мм, не более 1/5
диаметра сечения элемента и не более 100 мм; диаметр навивки спиралей или
диаметр колец следует принимать не менее 200 мм. 5.84(5.24). Сетки косвенного армирования могут быть сварными из пересекающихся
стержней или в виде гребенок (рис. 120). В обоих случаях должна
быть обеспечена совместная работа стержней сетки с бетоном. Рис. 119. Спиральное косвенное
армирование железобетонных элементов Рис. 120. Косвенное
армирование в виде пакета поперечных сварных сеток При применении косвенного
армирования сварными сетками должны соблюдаться следующие условия: а) площади сечения стержней
сетки на единицу длины в одном и в другом направлении не должны различаться
больше чем в 1,5 раза; б) шаг сеток (расстояние
между сетками в осях стержней одного направления) следует принимать не менее 60
мм, не более 1/3 меньшей стороны сечения элемента и не
более 150 мм; в) размеры ячеек сеток должны
назначаться не менее 45 мм, не более 1/4 меньшей стороны
сечения элемента и не более 100 мм. Первая сварная сетка
располагается на расстоянии 15 - 20 мм от нагруженной поверхности элемента. При усилении концевых
участков внецентренно-сжатых элементов сварные сетки косвенного армирования
должны устанавливаться у торца элемента числом не менее 4 шт. и располагаться
на длине (считая от торца элемента) не менее: 20d, если продольная арматура
выполняется из гладких стержней, и 10d, если она выполняется из
стержней периодического профиля (d - наибольший диаметр продольной арматуры). ОСОБЕННОСТИ СБОРНЫХ
КОНСТРУКЦИЙ
Общие
положения. Очертания изделий
5.85. Сборные железобетонные
изделия должны удовлетворять требованиям технологичности (удобства
изготовления): иметь простые очертания (с учетом в необходимых случаях
технологических уклонов), простое армирование и малую трудоемкость, допускать
механизацию и автоматизацию производства, возможность быстрого изготовления.
Они должны быть также удобны в транспортировании и монтаже. Железобетонные изделия
следует проектировать, как правило, для изготовления с формованием полностью за
один прием, т.е. без последующего добетонирования или сборки перед монтажом из
отдельных элементов. 5.86. Габариты и очертание сборных
конструкций должны соответствовать требованиям, изложенным в пп. 5.5 - 5.8. 5.87. Сборные железобетонные
изделия рекомендуется проектировать с учетом изготовления их по возможности в
максимально неразборных формах. Если невозможно изготовление
изделия в полностью неразборной форме, рекомендуется предусматривать
неразборной по возможности наибольшую поверхность формы. 5.88. Ребра в стенках балок
целесообразно предусматривать лишь при больших сосредоточенных нагрузках или
необходимости обеспечения устойчивости стенки. 5.89. Требования к точности
изготовления железобетонных элементов должны устанавливаться исходя из анализа
вида сопряжения этого элемента с другими элементами. Так, например, при
замоноличивании стыков бетоном в ряде случаев могут быть допущены более высокие
отклонения от номинальных размеров, компенсируемые укладываемым бетоном. Стыки элементов
сборных конструкций
5.90(5.42). При стыковании
железобетонных элементов сборных конструкций усилия от одного элемента к
другому передаются через стыкуемую рабочую арматуру, стальные закладные детали,
заполняемые бетоном швы, бетонные шпонки или (для сжатых элементов)
непосредственно через бетонные поверхности стыкуемых элементов. Для передачи значительных
сдвигающих усилий в стыке через заполняемые бетоном швы между сборными
элементами на стыкуемых поверхностях последних рекомендуется предусматривать
устройство насечки или фигурного, по возможности неармированного, профиля,
образуемого фигурной поверхностью формы. 5.91(5.43). Жесткие стыки сборных
конструкций должны, как правило, замоноличиваться путем заполнения швов между
элементами бетоном. Если при изготовлении элементов обеспечивается плотная
подгонка поверхностей друг к другу (например, путем использования торца одного
из стыкуемых элементов в качестве опалубки для торца другого), то допускается
при передаче через стык только сжимающего усилия выполнение стыков «насухо». 5.92. Рекомендуется принимать
такие конструктивные решения, при которых обеспечивается простота изготовления
стыковых деталей (закладных деталей, сеток и т.п.), их сборки и фиксации в
форме, формования изделия (удобство пробетонирования), а также простота монтажа
и соединения сборных железобетонных элементов. 5.93(5.44). Стыки элементов,
воспринимающие растягивающие усилия, должны выполняться: а) сваркой стальных закладных
деталей; б) сваркой выпусков арматуры. При проектировании стыков
элементов сборных конструкций должны предусматриваться такие соединения
закладных деталей, при которых не происходило бы разгибания их частей, а также
выколов бетона. Рис. 121. Жесткий стык
сборных колонн с ванной сваркой арматурных выпусков а -
при четырех угловых арматурных выпусках; б - при арматурных выпусках,
расположенных по периметру сечения; 1 - арматурные выпуски; 2
- бетон замоноличивания в подрезках; 3 - центрирующая прокладка (сетки
косвенного армирования в разрезах условно не показаны) 5.94. Жесткие стыки сборных колонн рекомендуется выполнять путем ванной
сварки выпусков продольной арматуры, расположенных в специальных подрезках, с
последующим замоноличиванием этих подрезок. В таких стыках между торцами
стыкуемых колонн должны предусматриваться центрирующий бетонный выступ либо
прокладка в виде стальной пластинки, заанкеренной в бетоне, или приваренной при
монтаже к распределительному листу закладной детали (рис. 75 и 121).
Центрирующая прокладка (бетонный выступ) принимается с размерами в плане не
более 1/4 соответствующего размера сечения колонны и
толщиной 20 - 25 мм. Форма и размеры подрезок
определяются числом стыкуемых стержней (рис. 121). Суммарная высота
подрезок принимается не менее 30 см и не менее 8d (d - диаметр выпусков). 5.95(5.46). На концевых участках
стыкуемых внецентренно-сжатых элементов (например, концы сборных колонн) должна
устанавливаться косвенная арматура в соответствии с указаниями пп. 5.82 - 5.84. Коэффициент насыщения
косвенной арматурой μск (см. п. 3.60) принимается на менее
0,0125. При необходимости сварными
сетками может армироваться и бетон замоноличивания в зоне подрезок. В зоне подрезок
устанавливается 1 - 2 замкнутых хомута, огибающих арматурные выпуски. Марка бетона замоноличивания
принимается не менее М 300. 5.96. Сварку стальных закладных
деталей следует проектировать в соответствии с требованиями главы СНиП по
проектированию стальных конструкций. Сварку выпусков арматуры следует
предусматривать согласно указаниям пп. 5.16 - 5.18. При конструировании сварных
стыков и закладных деталей должны предусматриваться способы сварки, не
вызывающие коробления стальных деталей стыка. 5.97(5.51). При проектировании элементов
сборных перекрытий должно предусматриваться устройство швов между ними,
заполняемых бетоном. Ширина швов должна назначаться из условия обеспечения
качественного их заполнения и должна составлять не менее 20 мм для элементов
высотой сечения до 250 мм и не менее 30 мм при элементах большей высоты. При этом должна быть
обеспечена возможность размещения стыкуемой арматуры и закладных деталей и их
высококачественной сварки. Марка бетона для заполнения
швов, передающих расчетные усилия, принимается в соответствии с указаниями п. 2.4. Для замоноличивания
труднодоступных или трудно контролируемых мест стыка рекомендуется заполнение
шва раствором или бетоном под давлением, а также применение расширяющегося
цемента. Строповочные
устройства
5.98. При проектировании сборных
железобетонных изделий следует предусматривать удобство захвата их
грузозахватными приспособлениями при снятии с формы, а также при
погрузочно-разгрузочных и монтажных работах. Способы и места захвата
следует назначать с учетом технологии изготовления и монтажа изделия, а также
его конструктивных особенностей. Изделие должно быть проверено
расчетом на условия работы при принятом способе и размещении мест захвата. 5.99.(5.52). В элементах сборных
конструкций должны предусматриваться мероприятия для захвата их при подъеме:
инвентарные монтажные вывинчивающиеся петли, строповочные отверстия со
стальными трубками, стационарные монтажные петли из арматурных стержней и т.п.
(рис. 122).
Петли для подъема должны выполняться из горячекатаной стали согласно
требованиям п. 2.18. Захват изделий рекомендуется
предусматривать по возможности без применения устройств, требующих расхода
стали, путем образования углублений, пазов, отверстий, а также использования
очертания изделия (рис. 122,а, б). Возможно сочетание двух видов устройств для
захвата, предназначенных для различных этапов перемещения изделия (рис. 122,в). 5.100. При проектировании изделий
со строповочными петлями следует применять унифицированные петли. При
отсутствии унифицированных петель с требуемыми характеристиками рекомендуется
конструировать петли типов, приведенных на рис. 123. В первую очередь
рекомендуется применять петли типов П1, П2 и П3, как более простые в
изготовлении. Петли типов П4 - П9 рекомендуется применять в тех случаях, когда
петли П1, П2 и П3 не размещаются в изделии. Рис. 122. Примеры
строповочных устройств без петель а -
схема строповки блоков; б -
образование строповочных отверстий в колонне путем закладки стальных трубок; в - пример сочетания двух строповочных
устройств в одном изделии; 1 - положение грузового стропа; 2
- вырез для захвата; 3 - отверстие для захвата при монтаже;
4 - закладная трубка; 5 - петля для захвата при извлечении
из формы Рис. 123. Рекомендуемые типы
строповочных петель а - из стали класса А-I или А-II, свободно размещаемые
в изделии; б, в - то же, размещаемые в стесненных условиях; б
- из стали класса А-I; в - то же, А-II Размеры петель рекомендуется
принимать из условий машинного производства. Рекомендуемые размеры петель с
прямыми и отогнутыми ветвями, наиболее часто используемых в проектировании,
приведены в табл. 45. Таблица 45
5.101. Диаметр стержня петли d следует принимать согласно табл. 46 в
зависимости от приходящегося на петлю нормативного усилия. 5.102. Высоту проушины петли hп, соответствующую размерам
чалочных крюков грузовых стропов, следует принимать равной: 60 мм + d при диаметре стержня петли от 6 до 18 мм; 80 мм + d » » » » 20
и 22 мм; 150 мм + d » » » » от 25 до 32 мм. Длину lа и глубину запуска hб концов ветвей петли в бетон
изделия рекомендуется принимать согласно табл. 47. Допускается уменьшать длину
запуска lа в соответствии с фактической нормативной нагрузкой
от собственного веса элемента Pнф, приходящейся на петлю, с
учетом коэффициента динамичности kд =
1,5 и
коэффициента, учитывающего сгиб петли k = 1,5, умножая длину lа на отношение Таблица 46
Таблица 47
Рис. 124. Рекомендуемые
размеры лунок для потайного расположения проушин строповочных петель при диаметре стержня петли 10 - 18 мм: R1 = 125, a = 30, b1 = 50, c = 30, l1 = 25, l2 = 30; при диаметре стержня петли 20 - 22 мм: R1 = 150, a = 40, b1 = 65, c = 35, l1 = 30, l2 = 30 (в мм) Ветви петли из стали класса
А-I должны заканчиваться
крюками. Расстояние между боковой
поверхностью хвостового участка крюка петли и поверхностью изделия, измеряемое
в плоскости крюка, должно приниматься не менее 4d. Если невозможно осуществить
необходимую длину и глубину запуска концов петли, анкеровка петли выполняется с
помощью специальных мероприятий, например приваркой к закладным деталям,
заведением за рабочую арматуру и т.д. Надежность принятой анкеровки петли
должна подтверждаться расчетом или испытаниями. 5.103. Для изделий, изготовление
которых может производиться с заглаживанием открытой грани механизированным
способом, рекомендуется предусматривать петли на других, необрабатываемых
гранях или располагать проушины петель ниже заглаживаемой грани в
углублениях-лунках по рис. 124. Для заведения чалочного крюка
стропа в проушину лунку следует располагать со смещением к середине изделия
относительно плоскости проушины. ЗАКЛАДНЫЕ ДЕТАЛИ
Общие
указания
5.104. При проектировании
железобетонных конструкций следует применять унифицированные, в том числе
штампованные закладные детали, утвержденные в установленном порядке. Если это
не удается, закладные детали следует проектировать в соответствии с указаниями,
приведенными ниже. 5.105(5.45). Закладные детали должны быть
заанкерены в бетоне с помощью анкерных стержней или приварены к рабочей
арматуре элементов. Закладные детали обычно состоят из пластин (отрезков
полосовой, угловой или фасонной стали) с приваренными к ним втавр или
внахлестку нормальными или касательными анкерами. Закладные детали могут иметь
также устройство для крепления к формам (например, отверстия в пластинах),
упоры для работы на сдвиг, арматурные коротыши, служащие для фиксации положения
рабочей арматуры или самой закладной детали, болты для соединения сборных
элементов и т.п. (рис. 125). 5.106. Для возможности
механизированного заглаживания поверхности железобетонного изделия пластины со
стороны этих поверхностей должны быть заглублены в бетон не менее чем на 5 мм. В больших пластинах закладных
деталей, находящихся при формовании сверху, следует предусматривать отверстия
для выхода воздуха и контроля качества бетонирования. 5.107. Проектное положение
закладных деталей (их фиксацию) в процессе бетонирования следует обеспечивать
временным креплением к форме или опалубке либо приваркой в кондукторах к
арматурным каркасам (рис. 125). Крепление к форме
рекомендуется, когда закладные детали находятся близко от элемента формы или
примыкают к нему. В других случаях следует предусматривать крепление к
арматурным изделиям, применяя в необходимых случаях соединительные стержни. 5.108. Если закладные детали
эксплуатируются в условиях, когда возможна коррозия стали (например, на
открытом воздухе, в стыках при отсутствии их надежного замоноличивания бетоном
или раствором и т.п.), следует предусматривать защиту их от коррозии в
соответствии с требованиями СНиП II-28-73. Характеристики
антикоррозионных покрытий должны указываться в рабочих чертежах изделий. Рис. 125. Примеры конструкций
закладных деталей а - деталь с касательными и нормальными анкерами; б - деталь типа
«двойной столик»; в -
детали типа «столик»; г -
детали с применением угловой стали; 1 - нормальные анкеры (приваренные
втавр); 2 - касательные анкеры (приваренные внахлестку); 3
- упор, работающий в двух направлениях; 4 - упор,
работающий в одном направлении; 5 - отверстие для фиксации 5.109. В рабочих чертежах изделий
расход стали на закладные детали должен подсчитываться отдельно от арматуры и
соединительных деталей. При этом в вес закладных деталей включаются вес анкеров
длиной не более 50d (в
случае, когда
закладная деталь включает и арматуру изделия) и соединительные стержни между
закладными деталями длиной не более 100d.
Рис. 126. Примеры фиксации
закладных деталей а, б - к борту формы; в -
к поддону; г - к
арматуре; 1 - винтовой фиксатор; 2 - закладная деталь; 3
- борт формы; 4 - болт; 5 - отверстие для
фиксации в пластине закладной детали; 6 - поддон формы; 7 - чека; 8 - шип с отверстием
для чеки; 9 - соединительный стержень; 10 - шплинтующая проволока, выходящая
на поверхность бетона (извлекается после уплотнения бетона). Чека - из
алюминиевой проволоки диаметром 3 мм Пластины
5.110. Назначение размеров пластин
и их профиля должно производиться из условий обеспечения: прочности и жесткости пластин
с учетом возможных эксцентрицитетов приложения нагрузок; размещения необходимого числа
анкеров с учетом положения примыкающих арматурных элементов; прочности и удобства
выполнения сварных соединений; размещения соединительных
накладок и монтажных сварных швов; положения закладных деталей в
изделии и положения изделий при монтаже с учетом допускаемых отклонений; удобства фиксации закладной
детали в форме; качественной укладки бетона; применения механизированного
заглаживания поверхностей железобетонного изделия. С целью унификации закладные
детали и стыки следует проектировать так, чтобы размеры пластин по возможности
не зависели от размеров сечений железобетонных элементов. Если размеры пластины
назначаются близкими к размеру сечения железобетонного элемента, следует
учитывать допускаемые плюсовые отклонения их размеров, предусмотренные
нормативными документами, и обеспечить возможность свободной установки
закладной детали при минусовых отклонениях размеров формы. 5.111(5.45). Толщина пластин закладных
деталей определяется в соответствии с указаниями п. 3.106 и требованиями сварки
(см. пп. 5.117
и 5.118). Толщина пластин сварных
закладных деталей должна приниматься не менее 6 мм, толщина стенок или полок
фасонного проката, к которым привариваются анкеры и соединительные детали - не
менее 5 мм. Для нерасчетных соединений допускается указанные выше минимальные
толщины снижать на 1 мм. Анкеры
5.112(5.45). Анкеры закладных деталей
следует проектировать преимущественно из арматуры классов А-II и А-III. Анкеры из стали класса А-I должны иметь на концах крюки, шайбы или высаженные
головки. Нормальные анкеры могут
применяться для передачи как осевых (вдоль анкера), так и боковых усилий,
касательные анкеры - только осевых усилий. Кроме касательных в закладной детали
должны предусматриваться также нормальные анкеры, сечение которых назначается
согласно указаниям пп. 3.104 и 3.105. Для обеспечения защитного
слоя бетона или возможности размещения анкера касательный анкер может иметь
отгиб до 30° от оси,
параллельной пластине. Допускается увеличение этого угла до 60° при обеспечении
радиуса загиба анкера R не менее 10d и до 90° при радиусе загиба не менее 20d. Загиб анкера должен начинаться на расстоянии не менее 2d от ближайшего края сварного соединения анкера с
пластиной (рис. 127). 5.113. При наличии прижимающего усилия (т.е. при N'ан > 0, см.
п. 3.104) допускается передача сдвигающих (касательных) усилий на бетон через
упоры из полосовой стали или круглых коротышей (рис. 125,в). Высоту упоров
рекомендуется принимать не менее 10 и не более 40 мм. Такое решение может
применяться при знакопеременных сдвигающих усилиях, если не представляется
возможным разместить касательные анкеры. При размещении упоров вблизи края
элемента должны приниматься меры против выкалывания бетона (косвенное
армирование и т.п.). Следует избегать применения
анкеров в виде отрезков полосовой или угловой стали, разделяющих бетон. 5.114. Выбор числа и диаметра анкеров должен производиться с учетом
равномерной передачи усилий на бетон, надежности анкеровки закладной детали, а
также трудоемкости изготовления и расхода стали на закладную деталь. Рис. 127. Приварка отогнутого
касательного анкера ручной электродуговой сваркой Рис. 128. Наименьшие
расстояния между анкерами закладной детали и от анкеров до края бетона а - при работе нормальных анкеров на осевые силы; б - то же, на
поперечные силы; в - при
работе касательных анкеров на осевые силы; г - то же, при отогнутых
усиленных анкерах. При анкерах из стали класса А-II: a = 4d, b = 6d, c = 3d, e = 8d; то же, класса А-III: a = 5d, b = 7d, c = 3,5d, e = 8d (d -
диаметр стержня, требуемый по расчету) С увеличением диаметра
анкеров возрастают усилия, раскалывающие бетон, и может потребоваться косвенное
армирование бетона. Число расчетных нормальных
анкеров при осевом растяжении их нормальной силой или при действии изгибающего
момента должно быть не менее четырех. Число расчетных нормальных
анкеров при поперечном загружении должно быть, как правило, не менее четырех,
но может быть уменьшено до двух, например при отсутствии изгибающего момента в
направлении сдвигающей силы перпендикулярно к плоскости, в которой расположены
анкеры. Число расчетных касательных
анкеров должно быть не менее двух. При этом должно предусматриваться также не
менее двух нормальных анкеров. Расстояния между осями
требуемых по расчету анкеров должны быть не менее величин, приведенных на рис. 128. 5.115(5.45). Длина анкерных стержней закладных деталей при действии на них
растягивающих сил должна быть не менее величины lан, определяемой по указаниям п. 5.48. Длина анкера отсчитывается:
для нормальных анкеров - от внутренней поверхности пластин; для касательных
анкеров - от начала отгиба или от торцевой кромки пластины. Для сборных железобетонных
конструкций заводского изготовления допускается длину анкеров принимать по
табл. 48,
но не менее 200 мм. Таблица 48
При действии на анкерные
стержни только сдвигающих или сжимающих усилий длина анкерных стержней может
приниматься на 5d меньше значений lан, определенных по формуле (308)
или по табл. 41,
но не менее минимальных величин lан согласно требованиям п. 5.48, а
для сборных элементов заводского изготовления - не менее 15d. 5.116(5.45).
Указанная в п. 5.115 длина анкерных стержней
может быть уменьшена при условии приварки на концах стержней анкерных пластин
или устройства высаженных горячим способом анкерных головок диаметром не менее 2d или обжатием шайб. В этих случаях длина анкерного стержня определяется
расчетом на выкалывание и смятие бетона и принимается не менее 10d (d - диаметр анкера). Анкерные пластины должны
удовлетворять требованиям п. 5.49,а. При возможности образования трещин
в бетоне вдоль анкеров (σб > Rр) устройство усилений на концах
анкеров в виде пластинок, шайб или высаженных головок обязательно. При определении длины
заготовок нормальных анкеров следует учитывать припуск на осадку при сварке,
который может приниматься равным диаметру анкера. Длину заготовок следует
назначать кратной 10 мм. Сварные соединения
закладных деталей
5.117. Сварные соединения анкеров с пластинами втавр должны проектироваться в
соответствии с указаниями табл. 49. Рекомендуется
предусматривать дуговую сварку втавр под слоем флюса или контактную
рельефно-точечную сварку. Ручную дуговую сварку в
раззенкованные отверстия из-за большой трудоемкости следует применять при
невозможности использовать рекомендуемые способы сварки. 5.118. Сварные соединения анкеров и арматурных стержней с пластинами
внахлестку должны проектироваться в соответствии с указаниями табл. 50. Рекомендуется
преимущественное применение контактной рельефно-точечной сварки. Сварные швы при сварке
элементов пластин между собой должны назначаться по нормам проектирования
стальных конструкций. 5.119. Для закладных деталей
сборных железобетонных конструкций, подвергающихся действию вибрационных
нагрузок, применение рельефно-точечной сварки не допускается. 5.120. Во избежание поджога
стержней при ручной дуговой сварке швы должны начинаться с пластины и
выводиться на пластину, а места прихваток - провариваться. При назначении
размеров пластин необходимо это учитывать в соответствии с указаниями,
приведенными на рис. 129. Рис. 129. Ручная дуговая
сварка внахлестку фланговыми швами Таблица 49
Таблица 50
Рис. 130. Фиксирующие
устройства однократного использования. Примеры устройств, обеспечивающих
требуемую толщину (s) защитного слоя бетона а, б, в - фиксаторы с большой поверхностью контакта с
формой, изготовляемые из цементно-песчаного раствора; г - фиксаторы с минимальной
поверхностью контакта с формой, изготовляемые из цементно-песчаного раствора; д - то же, из асбестоцемента; е, ж, з - то же из
пластмасс (перфорированные); и -
то же, из алюминиевой перфорированной полосы; к, л, м - то же, из арматурной стали; 1
- рабочая поверхность формы; 2
- фиксатор; 3 - фиксируемая арматура; 4 - скрутка из вязальной проволоки; 5
- вязальная проволока, заделанная в фиксатор; 6 - эластичное
кольцо; 7 - упоры, привариваемые к арматуре ФИКСАЦИЯ АРМАТУРЫ
5.121(5.49).
Соответствие расположения арматуры ее
проектному положению должно обеспечиваться специальными мероприятиями, т.е.
применением средств фиксации. Фиксацию арматуры
рекомендуется осуществлять с помощью: устройств однократного
использования, остающихся в бетоне; инвентарных приспособлений,
извлекаемых из бетона до или после его твердения; специальных деталей,
прикрепленных к рабочей поверхности формы или опалубки и не препятствующих
извлечению железобетонного элемента из формы или снятию с него опалубки. 5.122. Средства фиксации арматуры
следует назначать с учетом: конструктивных особенностей
элемента; расположения арматуры
относительно граней рабочей поверхности формы или опалубки; условий эксплуатации элемента
в сооружении. 5.123. Рекомендуется применение
следующих фиксаторов однократного использования: для обеспечения требуемой
толщины защитного слоя бетона для арматуры - по рис. 130; для обеспечения требуемого
расстояния между отдельными арматурными изделиями или стержнями - по рис. 131; для обеспечения одновременно
обоих требований, указанных выше, - по рис. 132. Рис. 131. Фиксирующие
устройства однократного использования а, б, в - обеспечивающие требуемое расстояние между
отдельными арматурными изделиями; г - то же, стержнями; 1 - разделитель из арматурной стали,
устанавливаемый между рядами сеток; 2 - фиксатор подкладка для
обеспечения защитного слоя бетона; 3 - удлиненные поперечные стержни
каркаса, загибаемые вокруг стержней сетки; 4 - фиксатор для соединения
перекрещивающихся стержней (пространственная спираль из пружинной проволоки) Рис. 132. Фиксирующие
устройства однократного использования, обеспечивающие одновременно толщину
защитного слоя бетона и расстояние между отдельными арматурными элементами а - в плоских плитах; б, в - в балках прямоугольного сечения; г
- в элементах кольцевого сечения; 1 - фиксатор типа П-образного каркаса;
2 - горизонтальные арматурные сетки; 3 - рабочая
поверхность формы; 4 - фиксатор типа гребенки; 5
- вертикальная арматурная сетка; 6 - фиксаторы-стержни, дополнительно
привариваемые к каркасам; 7 - фиксатор типа накидной скобы из арматурной
проволоки; 8 - концентрически расположенные каркасы Вид фиксатора для обеспечения
толщины защитного слоя бетона у лицевых граней элементов следует выбирать
согласно рекомендациям, приведенным в табл. 51. Не допускается применение в
качестве подкладок обрезков арматурных стержней, полос и т.п. В растянутой зоне бетона
элементов, эксплуатируемых в условиях агрессивной среды, не допускается
установка пластмассовых подкладок под стержни рабочей арматуры или вплотную к
ним - под стержни распределительной арматуры. В таких изделиях следует
применять преимущественно подкладки из плотного цементно-песчаного раствора,
бетона или асбестоцемента. 5.124. В случае применения фиксаторов однократного использования следует, в
соответствии с требованиями табл. 51, указывать в рабочих
чертежах, какие из этих фиксаторов допускаются в данном элементе. Толщину защитного слоя бетона
в месте установки фиксатора-подкладки рекомендуется принимать кратной 5 мм. Таблица 51
Для фиксаторов однократного
использования, выполняемых из арматурной стали, следует приводить чертежи. На
рабочих чертежах арматурных изделий и в случае необходимости на чертежах общих
видов армирования железобетонных элементов следует показывать расположение этих
фиксаторов или опорных стержней, а в спецификациях - предусматривать расход
стали на их изготовление. Расположение и число
неметаллических фиксаторов - подкладок в рабочих чертежах допускается не
приводить. ОТДЕЛЬНЫЕ
КОНСТРУКТИВНЫЕ ТРЕБОВАНИЯ
5.125(5.47). Осадочные швы должны
предусматриваться в случаях возведения здания (сооружения) на неоднородных
грунтах основания (просадочных и др.), в местах резкого изменения нагрузок и
т.п. Осадочные швы, а также
температурно-усадочные швы в сплошных бетонных и железобетонных конструкциях
должны осуществляться сквозными с разрезом конструкции до подошвы фундамента.
Температурно-усадочные швы в железобетонных каркасах осуществляются посредством
двойных колонн с доведением шва до верха фундамента. Расстояния между
температурно-усадочными швами в бетонных фундаментах и стенках подвалов
допускается принимать в соответствии с расстояниями между швами, принятыми для
вышележащих конструкций. 5.126(5.48).
В бетонных конструкциях должно
предусматриваться конструктивное армирование в следующих случаях: а) в местах резкого изменения
размеров сечения элементов; б) в местах изменения высоты
стен (на участке не менее 1 м); в) в бетонных стенах под и
над проемами каждого этажа; г) в конструкциях,
подвергающихся воздействию динамической нагрузки; д) у растянутой или менее
сжатой грани внецентренно-сжатых элементов, если в сечении возникают
растягивающие напряжения или сжимающие напряжения менее 10 кгс/см2,
при наибольших сжимающих напряжениях более 0,8Rпр (напряжения определяются как для упругого тела); при
этом коэффициент армирования μ принимается равным или более 0,025 %. Требования настоящего пункта
не распространяются на элементы сборных конструкций, проверяемые в стадии
транспортирования и монтажа; в этом случае необходимое армирование определяется
расчетом по прочности на усилия, возникающие при транспортировании и монтаже. Если расчетом установлено,
что прочность элемента исчерпывается одновременно с образованием трещин в
бетоне растянутой зоны, то следует учитывать требования п. 1.18 для
слабоармированных элементов (без учета работы растянутого бетона). Если,
согласно расчету с учетом сопротивления растянутой зоны бетона, арматура не
требуется и опытом доказана возможность транспортирования и монтажа таких
элементов без арматуры, конструктивная арматура не предусматривается. ТРЕБОВАНИЯ,
УКАЗЫВАЕМЫЕ НА РАБОЧИХ ЧЕРТЕЖАХ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ
Общие
требования
5.127. В рабочих чертежах железобетонных конструкций или в пояснительной
записке к ним должны быть указаны следующие общие требования: а) проектная марка бетона по
прочности на сжатие и в случаях, предусмотренных в п. 2.5, марка бетона по
морозостойкости и водонепроницаемости; б) вид арматуры (стержневая
или проволочная) и ее профиль; класс арматуры, а в необходимых случаях
(например, для конструкций, работающих при низких температурах или
рассчитываемых на выносливость) и марка стали; номер ГОСТа, а при его
отсутствии - номера технических условий на данный вид стали; ГОСТы или
технические условия на товарные арматурные изделия (сетки или каркасы), если
таковые применяются, условия работы сварных соединений (низкие температуры или
переменные нагрузки); соответствующие нормативные документы по сварке; в
сложных случаях - методы изготовления пространственного арматурного каркаса и
порядок его сборки; в) мероприятия по
антикоррозионной защите и по защите от воздействия высоких температур, если
таковые необходимы; г) толщина защитного слоя
бетона для рабочей арматуры, а также необходимость установки соответствующих
фиксаторов, обеспечивающих проектное положение арматуры и их виды; д) расчетные схемы, нагрузки;
по возможности - нормативные и расчетные усилия в основных сечениях. Дополнительные
требования, указываемые на рабочих чертежах сборных элементов
5.128. В рабочих чертежах элементов
сборных конструкций или в пояснительной записке к ним кроме данных,
перечисленных в п. 5.127, должны быть указаны: наименьшие размеры опорных
участков; степень (качество) отделки
поверхности (при необходимости); места для захвата элементов
при подъеме и монтаже (в случае необходимости - и при снятии с формы), места их
опирания при транспортировании и складировании; требования о нанесении заводом-изготовителем
меток (рисок), необходимых для обеспечения качественной укрупнительной сборки
конструкций, а для элементов с трудноразличимым верхом или торцами (например,
прямоугольного сечения с одиночным или несимметричным двойным армированием) - требования
о нанесении заводом-изготовителем маркировки (надписи), обеспечивающей
правильность положения таких элементов при их подъеме, транспортировании и
укладке; для элементов, образцы
которых, согласно требованиям ГОСТ 8829-77 «Конструкции и изделия железобетонные
сборные. Методы испытаний и оценки прочности, жесткости и трещиностойкости» или
других нормативных документов, испытываются загружением, должны указываться
схемы испытания, величины нагрузок, прогибов и других контролируемых величин; масса сборного элемента. Требования к
оформлению рабочих чертежей
5.129. Система оформления рабочих
чертежей железобетонных конструкций должна обеспечивать удобство пользования
чертежами на каждом технологическом переделе производства как в случае
возведения монолитных железобетонных конструкций, так и в случае заводского
изготовления и монтажа железобетонных изделий. Рабочий чертеж следует
ориентировать на определенных исполнителей и службы. Должна быть обеспечена
возможность передачи отдельных листов рабочих чертежей на технологические
переделы без доработки, перечерчивания или составления дополнительных эскизов. 5.130. Целесообразно разделение
альбома рабочих чертежей на две части: 1) общие виды конструкций, узлы,
монтажные схемы армирования и т.п.; 2) рабочие чертежи арматурных элементов и
закладных деталей. Рабочие чертежи каждого
арматурного элемента или закладной детали выполняются на отдельных листах
(форматках). Рабочие чертежи сложных
арматурных изделий рекомендуется оформлять в виде ряда деталировочных чертежей,
каждый из которых предназначен для выполнения определенных операций
(изготовление сеток, сборка сеток в пространственные каркасы и т.п.). 5.131. В рабочих чертежах
железобетонных изделий массового производства рекомендуется приводить варианты
отдельных конструктивных решений, учитывающих особенности технологии, в
частности технологических уклонов, классов и марок стали, конструктивных
решений арматурных элементов и закладных деталей. Должны быть даны указания,
позволяющие производить замену отсутствующих профилей наиболее употребляемой в
проекте арматуры без существенного ее перерасхода. Условные обозначения арматуры
на чертежах
ПРИЛОЖЕНИЕ 1
ЗНАЧЕНИЯ
υ И A ДЛЯ РАСЧЕТА ПРОЧНОСТИ ИЗГИБАЕМЫХ
ЭЛЕМЕНТОВ
ПРИЛОЖЕНИЕ 2
СОРТАМЕНТ
АРМАТУРЫ
СОДЕРЖАНИЕ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
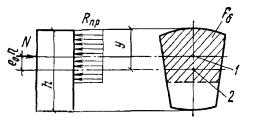
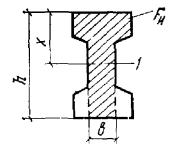
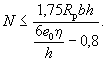
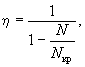
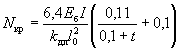
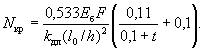
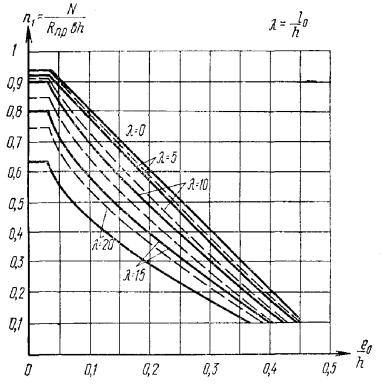
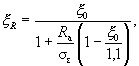
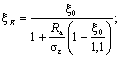
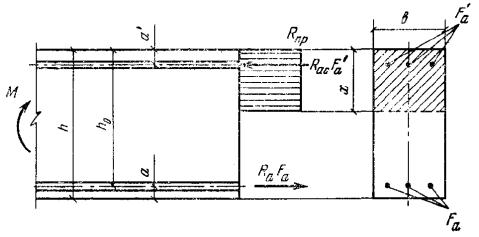
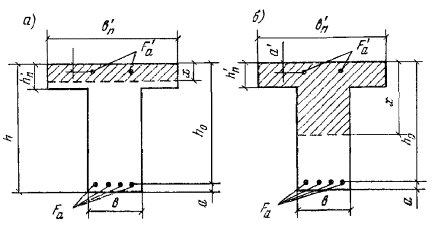
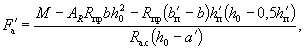
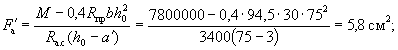
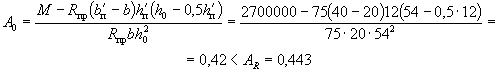
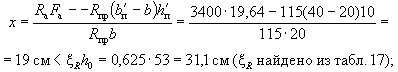
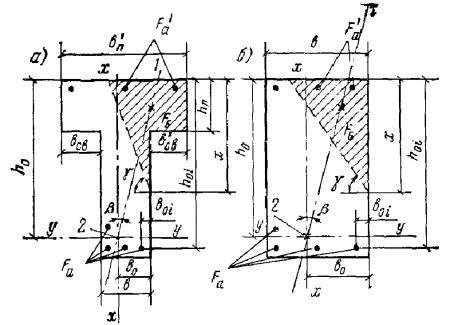
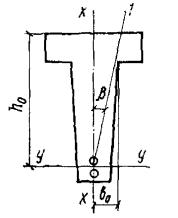
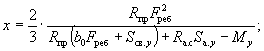
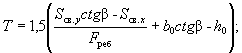
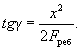
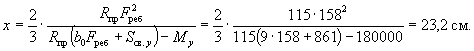
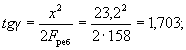
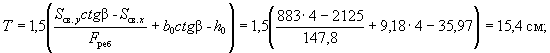
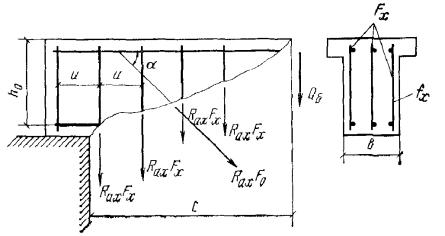
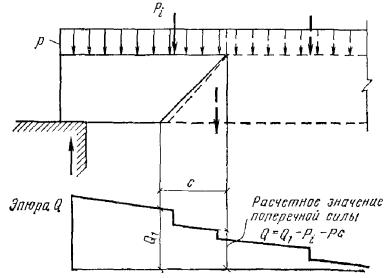
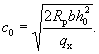
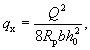
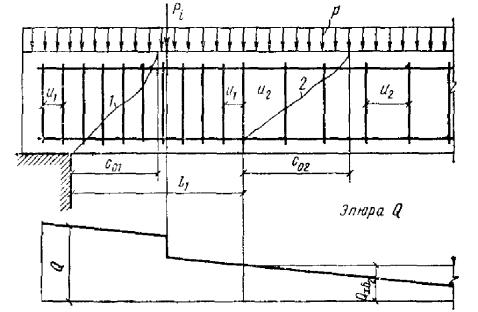
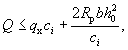
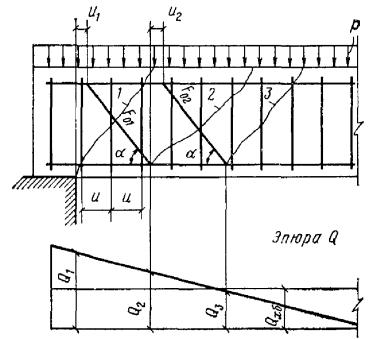
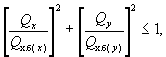
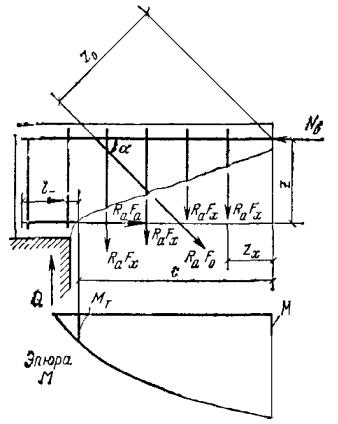
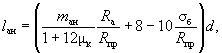
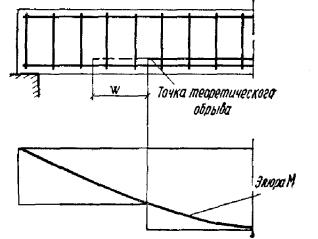
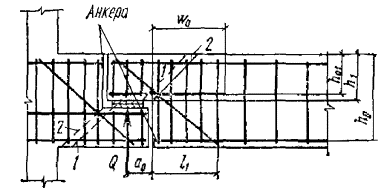
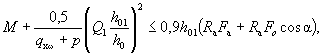
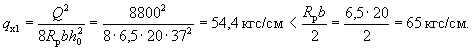
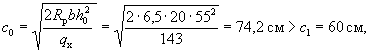
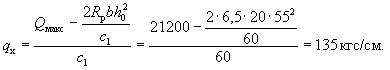
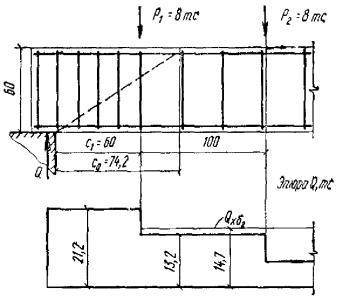
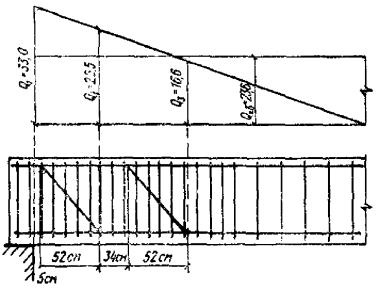
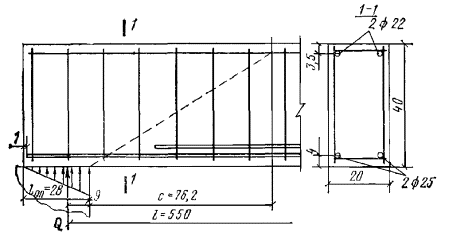
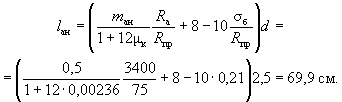
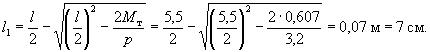
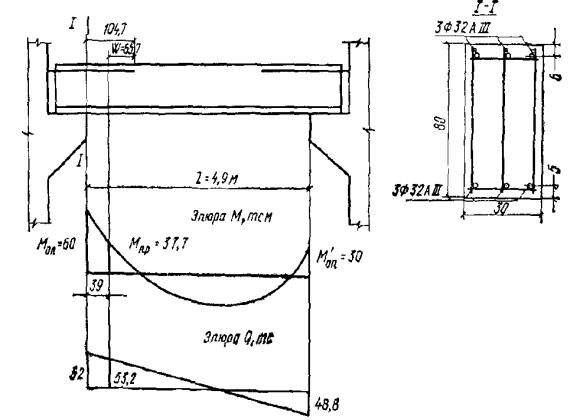
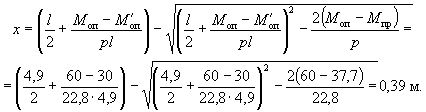
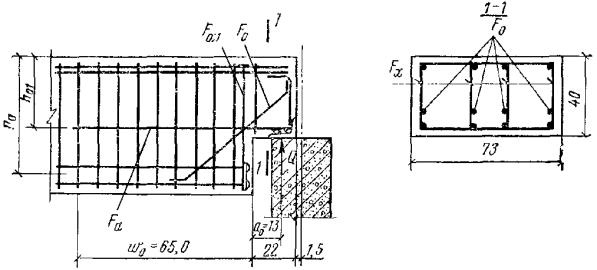
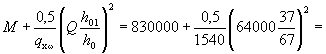
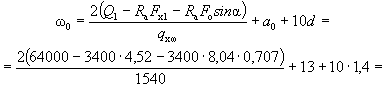
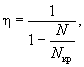
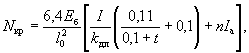
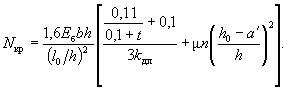
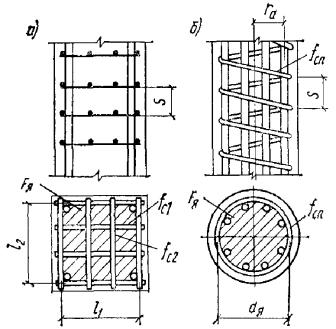
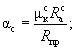
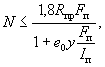
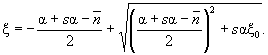
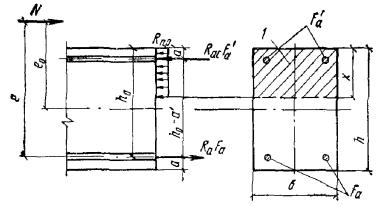
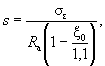
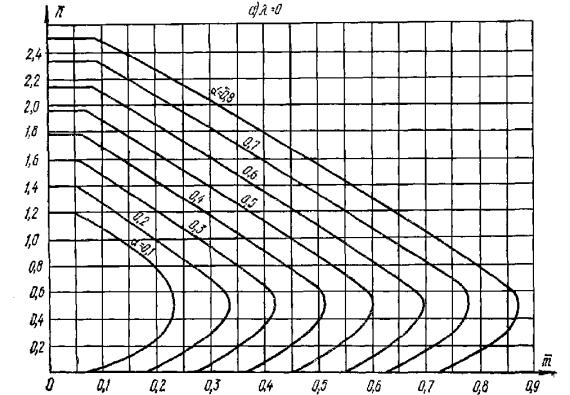
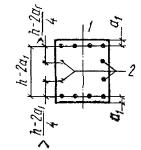
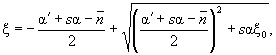
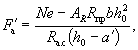
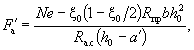
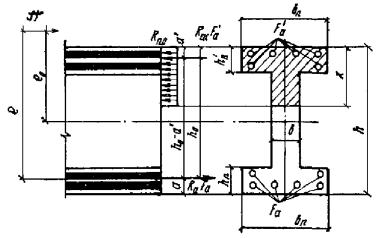
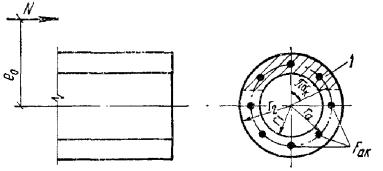
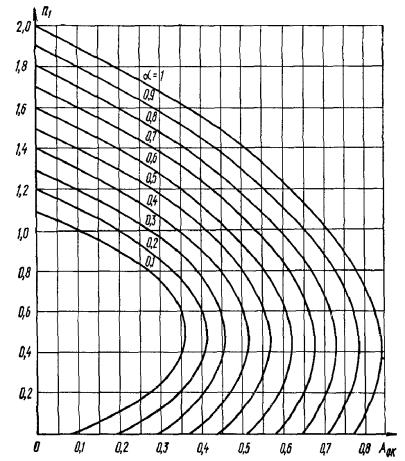
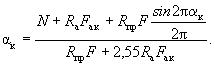
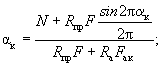
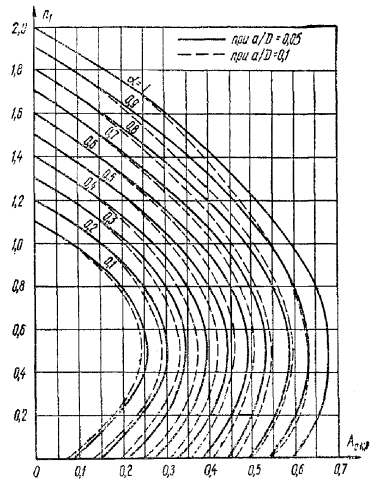
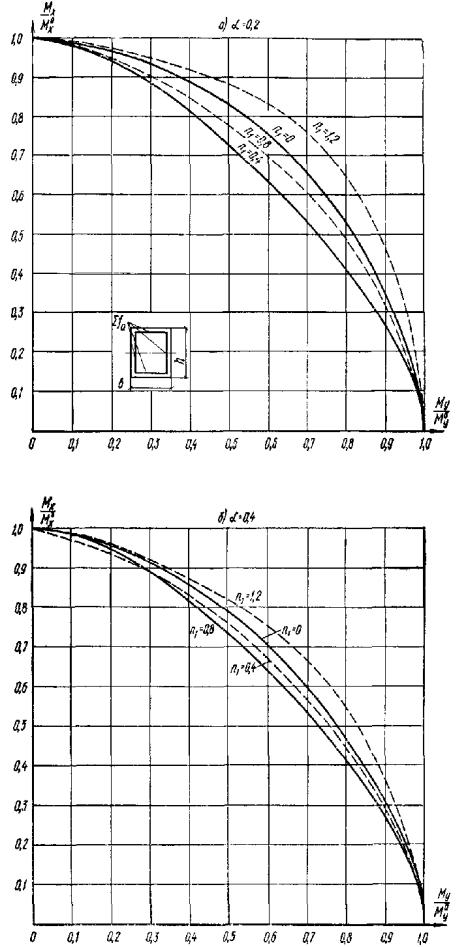
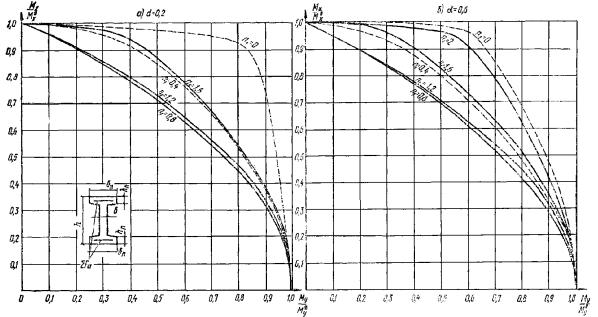
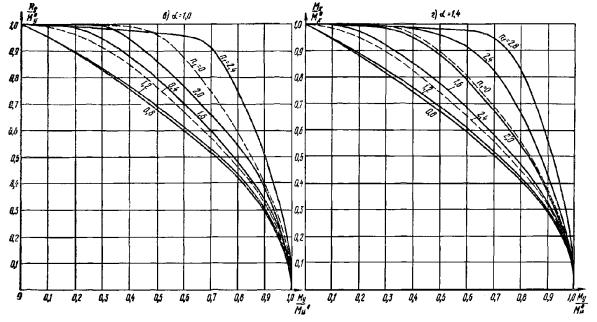
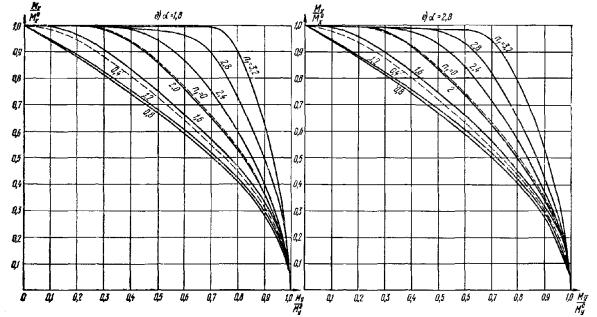
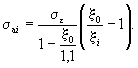

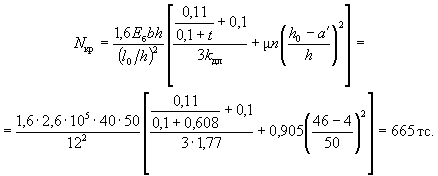
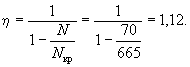
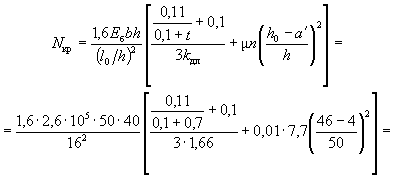
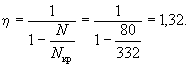
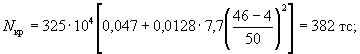
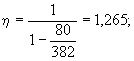
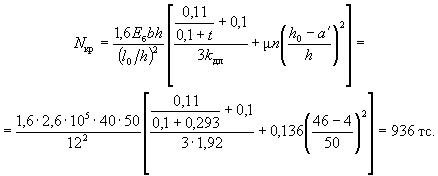
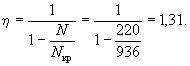
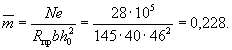
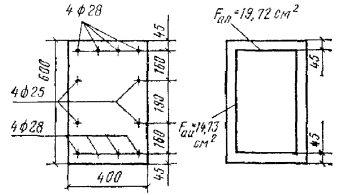
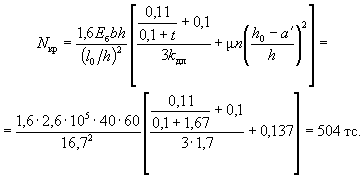
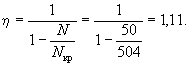
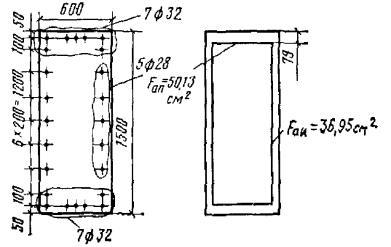
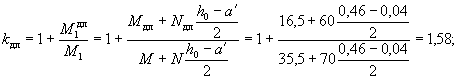
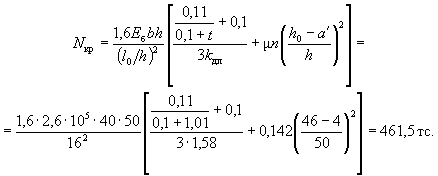
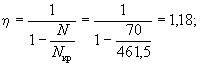
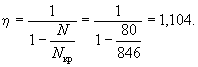
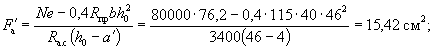
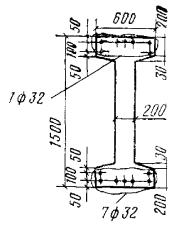
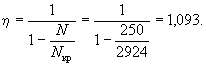
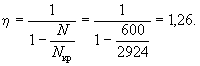
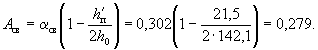
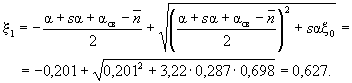
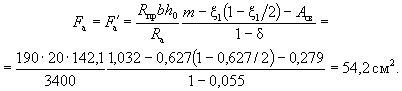
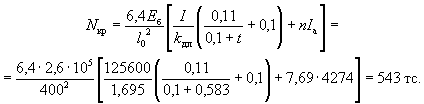
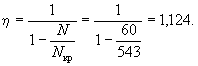
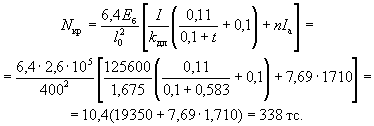
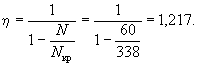
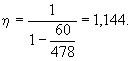
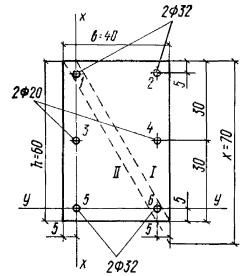
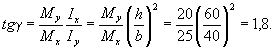
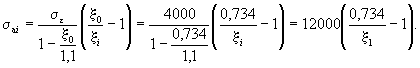
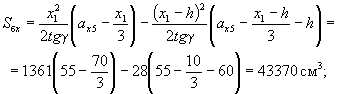
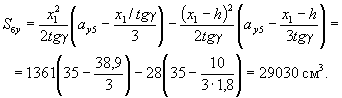
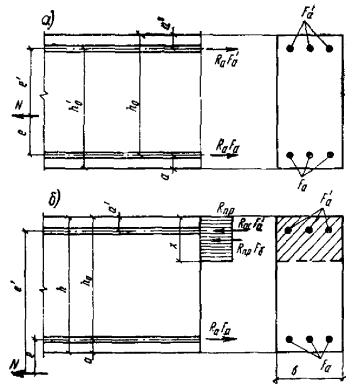
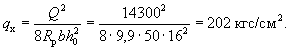
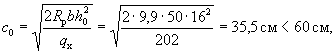
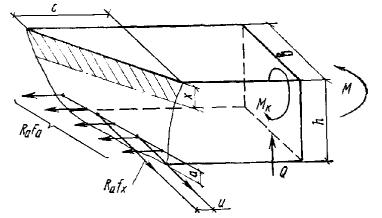
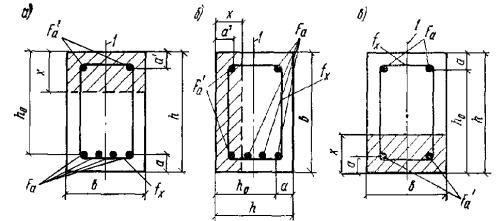
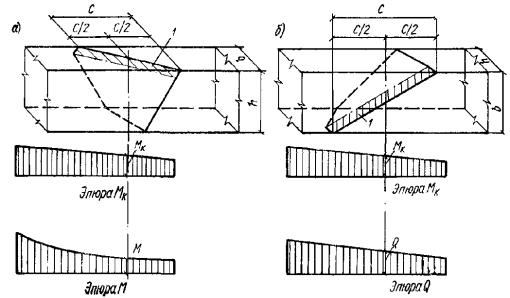
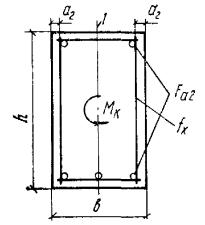
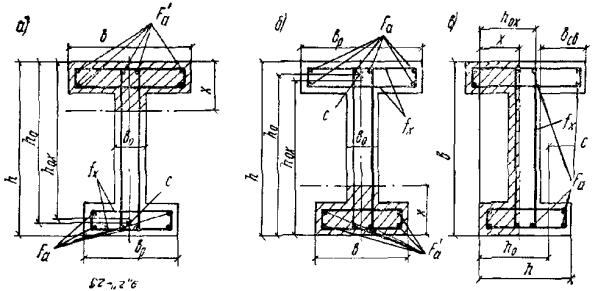
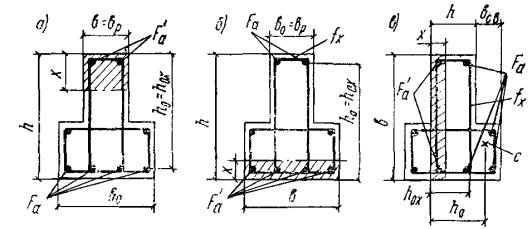
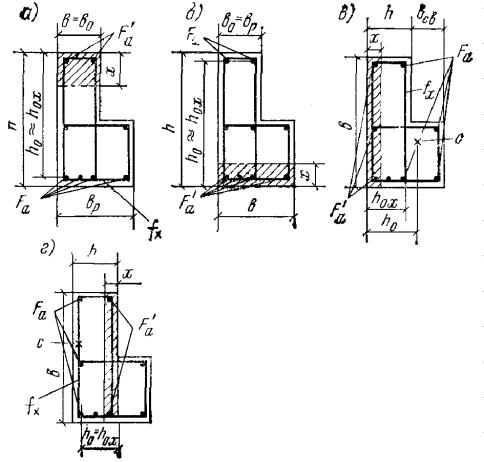
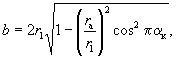
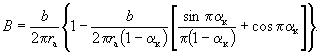
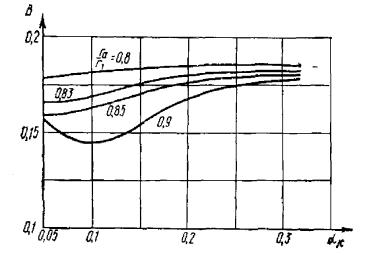
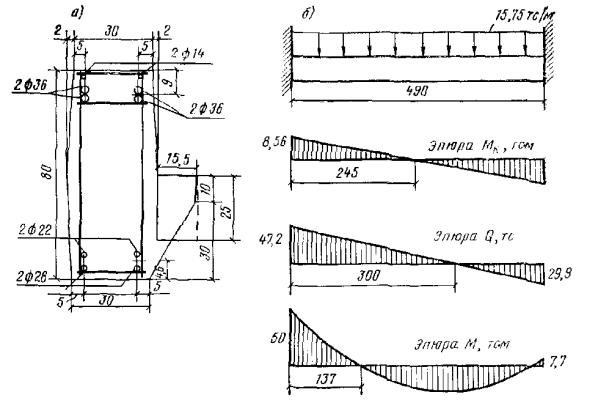
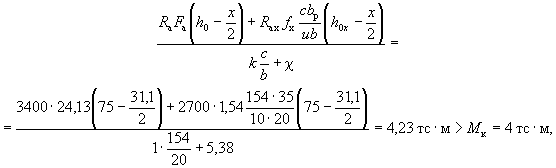
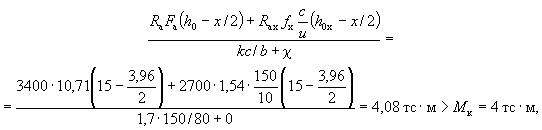
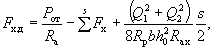
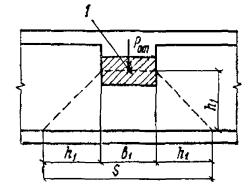
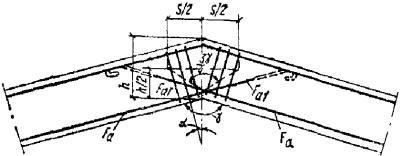
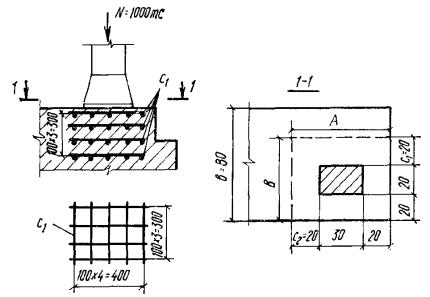
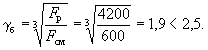
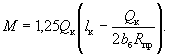
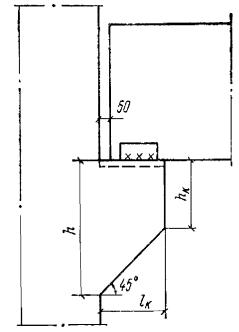
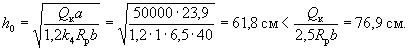
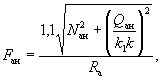
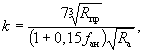
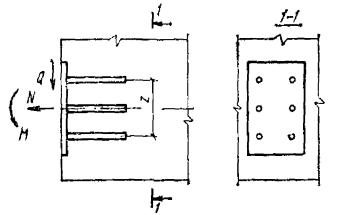
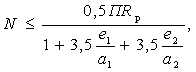
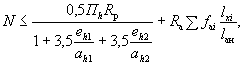
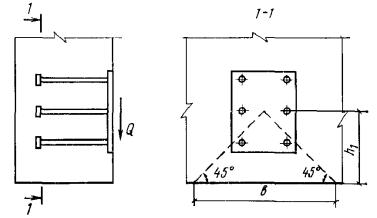
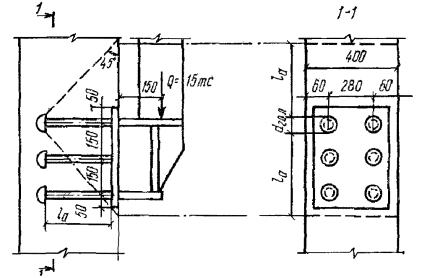
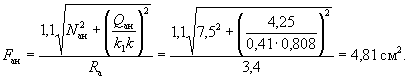
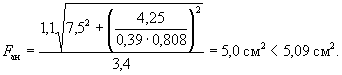
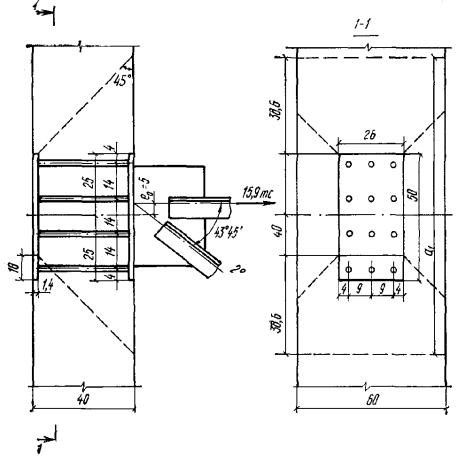
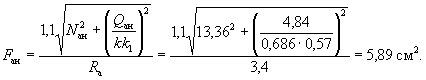
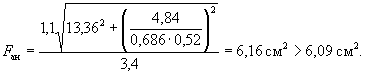
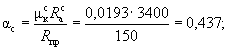
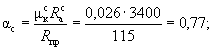
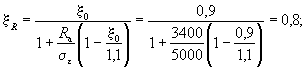
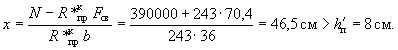
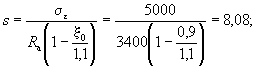
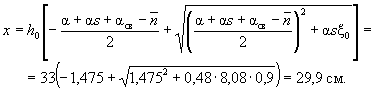
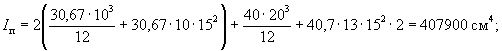
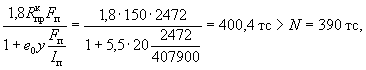
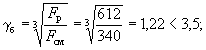
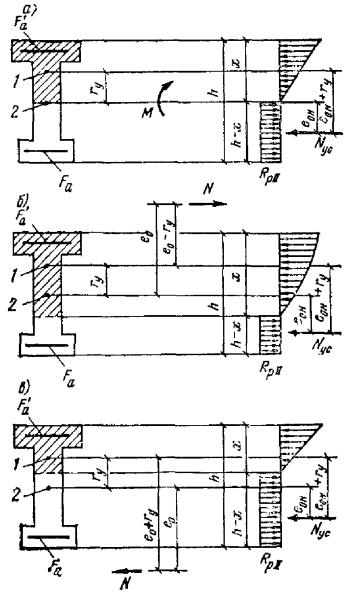
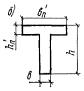
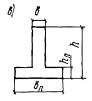
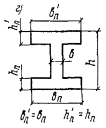
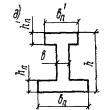
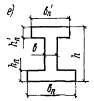
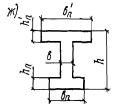
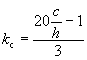
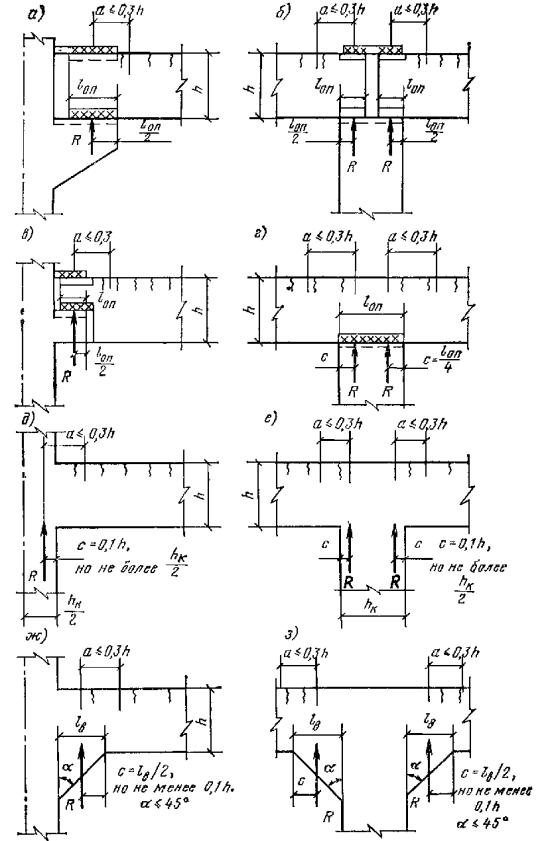
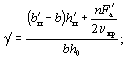
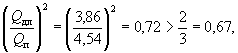
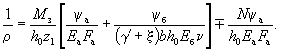
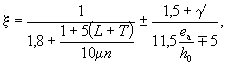
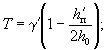
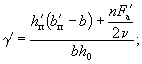

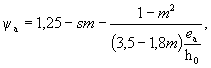
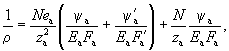
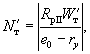
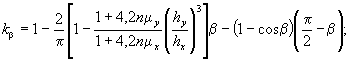
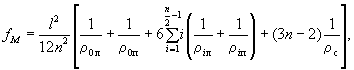
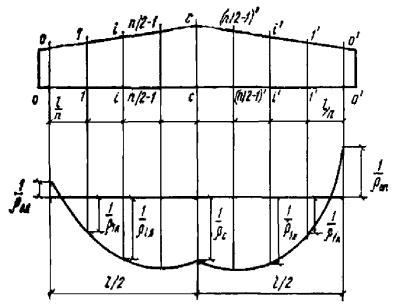
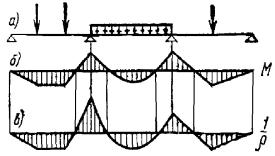
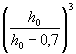 , принимаемый не более 1,5, где
, принимаемый не более 1,5, где